Глава 4. Каустики лагранжевых отображений гелевой оксигидратной магнитной жидкости железа

4.1 Введение

Потоки стохастических каустиков гелевых систем, например, магнитной жидкости железа (II;III) не есть системы оптические. Модели, в которых рассматриваются неупругие соударения, предполагают формирование ударных волн в местах их взаимодействия. Это явление по сути своей есть гелевая волновая интерференции или дифракции. При этом создаются многообразия движущиеся волновых фронтов, установленных экспериментально. Перестройки этих фронтов суть перестройки оксигидратных каустик, исследуемых в “пространстве-времени”. Объединение фронтов в различные моменты времени образует некую гиперповерхность в пространстве-времени. Эта гиперповерхность, образованная типичным движущимся фронтом, сама является фронтом типичного лежандрова многообразия. Это многообразие материальная основа формирования гелевых первичных структурированных кластеров.

Эволюция многих систем, в том числе и коллоидных, может быть описана системой обыкновенных дифференциальных уравнений [1, 2]

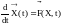, (4.1.1)

где 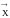- вектор в фазовом пространстве, 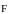- векторное поле над этим пространством. Именно такой вид имеют законы, управляющие поведением различных осцилляторов, в том числе и генератора Ван-дер-Поля. Система дифференциальных уравнений, например, система (1) называется потоком в Rⁿ . Если не зависит явно от времени, а зависит только от 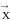( 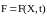), то поток называется автономным. Найти аналитическое выражение для уравнений (4.1.1) удается лишь в отдельных частных случаях, когда поток интегрируем.

Рассмотрим соответствующую потоку траекторию в фазовом пространстве. Упрощая задачу, используем подход, развитый Анри Пуанкаре. Вместо прямого изучения решения системы уравнений (4.1.1) в R³ просто рассмотрим точки пересечения траектории с плоскостью. Отметим, что точки пересечения соответствуют заданному направлению эволюции. Выбираем плоскость 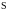, заданную уравнением 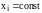, и отмечаем точки пересечения траектории орбиты 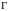(решения уравнения (1) с плоскостью , соответствующие заданному направлению эволюции (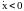 ). Траектория 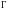пересекает 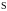в точках .

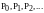Таким образом, можно получить множество точек, образующих сечение Пуанкаре, то есть граф в двух измерениях. В оксигидратных гелях мы имеем дело именно с ионными потоковыми движениями. Даже при достаточно низкой температуре (Т 298К) поляризованные ДЭС макромолекул, имеющих пептизационно-полимеризационные конформеры, при развитии во времени либо разрушаются (“разрываются”) с выплеском ионно-молекулярных потоков, либо поглощают их. Причины этого – чисто термодинамические, при макромолекулярных пептизационно-полимеризационно-конформерных перестройках энергия ДЭС, окружающих их, стремится к минимизации. Это достигается либо выплеском ионных потоков, либо их связыванием (причем, в узких областях пространства, то есть в условиях далеких от равновесия).

Таким образом, в гелевых образцах оксигидрата иттрия, циркония и других наблюдается сложная система конформерного движения самих макромолекулярных образований и потокового ионно-кластерно-молекулярного движения внутри них (в условиях далеких от равновесия). В качестве отображающей плоскости принимается или графитовый, или платиновый электроды, на которых замыкается ионно-молекулярный кластерный поток (“протыкает” их).

Лагранжево расслоение имеют естественную аффинную структуру: сдвиги определены потоками кластеров, порожденными функциями Гамильтона [3]. Пусть интегрируемая система с интегралами 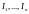имеет компактное, регулярное интегральное 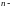подмногообразие 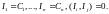В некоторой окрестности этого многообразия отображение 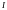является лагранжевым расслоением. Следовательно, инвариантные торы интегрируемых систем образуют лагранжевы расслоения. Аффинная структура на слоях является главным ингредиентом конструкции переменных действие – угол для интегрируемых систем, которые образуют фазовые портреты или аттракторы.

Рассмотрим вложение лагранжево многообразие 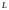в пространстве лагранжева расслоения 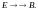Проекция в 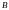называется лагранжевым отображением. Таким образом, лагранжево отображение есть тройка 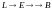, где левая стрелка является лагранжевой иммерсией, а правая – лагранжевым расслоением, рис.4.1.

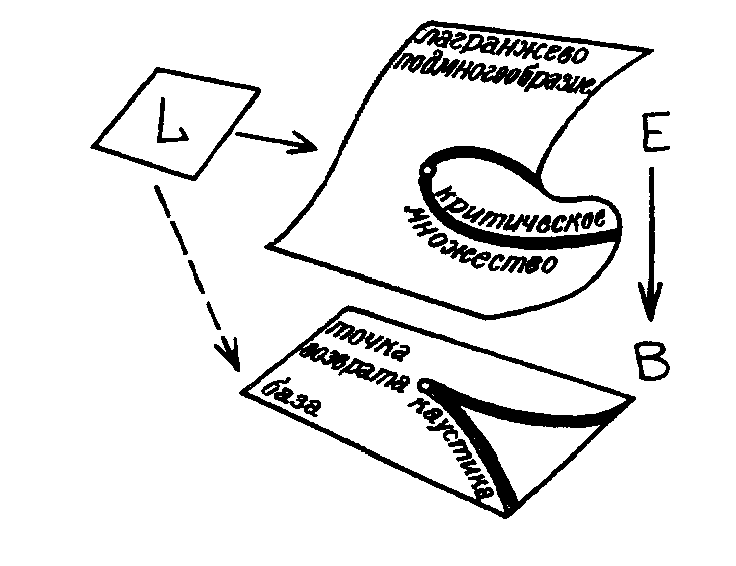
Рис.4.1

Лагранжево отображение и его каустика

Множество критических значений лагранжева отображения называется его каустикой. Каустики эквивалентных отображений всегда диффеоморфны.

В соответствии с представлениями [3] рассмотрим следующее:

Градиентное отображение. 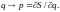Лагранжево подмногообразие является графиком этого отображения.

Нормальное отображение. Сопоставим каждому вектору нормали к подмногообразию его конечную точку. Примерно именно подобным образом (то есть нормально) мы в наших экспериментах размещаем электропроводящие графитовые плоскости. Получившееся отображение – лагранжево подмногообразие (лагранжево подмногообразие в 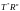образовано 1-формами 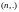в конечных точках нормальных векторов ). Каустика этого отображения является огибающей семейства нормалей к исходному подмногообразию. Эта каустика для гиперповерхности также называется фокальным множеством гиперповерхности.

Отображение Гаусса. Это отображение трансверсально ориентированной гиперповерхности евклидова пространства в единичную сферу, при этом точка гиперповерхности отправляет единичную нормаль к гиперповерхности в этой точке. Отображение Гаусса лагранжево. Лагранжево подмногообразие симплектического многообразия ориентированных прямых в евклидовом пространстве образовано нормалями к гиперповерхности.

Названные обстоятельства явились мотивирующими обстоятельствами для создания теории лагранжевых особенностей по аналогии с общей теорией особенностей Уитни [4].

Лагранжевы особенности. По определению лагранжева особенность есть росток лагранжева отображения, рассматриваемый с точностью до лаграгнжевой эквивалентности.

Важными физическими явлениями, в которых встречаются лагранжевы особенности, являются каустики излучения, например, световые и им подобные.

Кластерные ионно-потоковые каустики также являются каустиками типа излучения, как нам представляется. Пусть 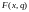обозначает оптическое (или некое излучательное) расстояние от точки

(например, когерентного) источника излучения на гладком многообразии до точки 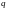многообразия наблюдения. Фазы волн на многообразии наблюдения определяются лагранжевым многообразием (рис.4.2)

(4.1.2)

Семейство 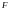функций переменной , определяемых параметрами , называется производящим семейством этого лагранжева подмногообразия (и его лагранжева отображения на многообразие наблюдения). Каустики таких лагранжевых отображений – это места, где яркость рефлексных проявлений максимальна.

На основании общей теории лагранжевых особенности типичных лагранжевых отображений многообразий размерности 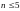содержатся в следующем списке лагранжевых особенностей, определенных производящими семействами 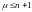[3]:

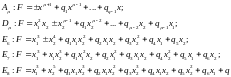
Все особенности , определенные этими производящими семействами, устойчивы и просты (не имеют модулей). Простейшие особенности 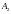(складка) и 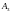(сборка) явным образом задаются проекцией лагранжевых многообразий:

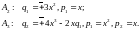
Обе складки (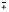 в ) лагранжево эквивалентны, в отличие от лагранжевых сборок ( в ).

Таким образом, типичные лагранжевы 2-поверхности в фазовом пространстве аттракторов определяют, при проекции на конфигурационную 2-плоскость, те же особенности Уитни, что и типичные (не лагранжевы) 2-поверхности. Это не очевидно априори, так как лагранжевы отображения достаточно специфичны. Есть отличия между типичными лагранжевыми и общими отображениями: а именно - некоторые типичные общие особенности не встречаются у лагранжевых особенностей, в то время как некоторые типичные лагранжевы особенности не являются типичными для (не лагранжевых) общих особенностей.

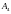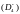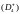Типичная одномерная каустика имеет (помимо самопересечений) только полукубические точки возврата (особенности ). Типичная двумерная каустика имеет (помимо самопересечений) только ласточкины хвосты ( ), пирамиды , и кошельки , рис.4.2. Эти D особенности были названы “омбилическими особенностями”, так как они связаны с омбилическими точками на 2-поверхностях в евклидовом 3-пространстве. Они являются особенностями фокальных множеств поверхностей.

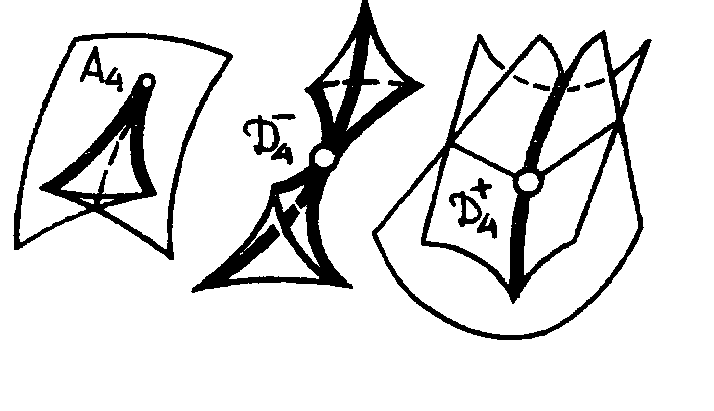
Рис.4.2

Типичные особенности каустик в трехмерном пространстве

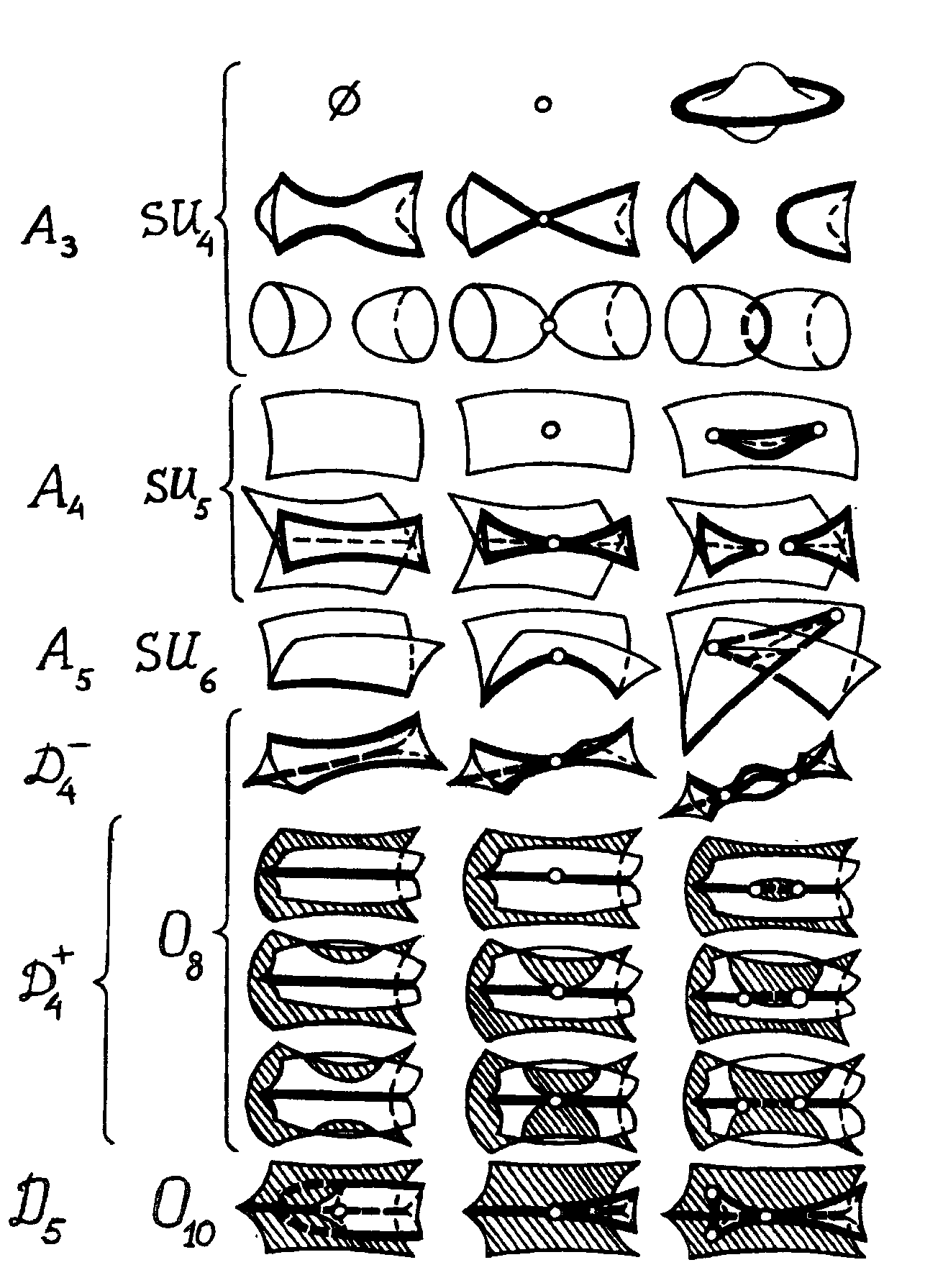
Рис.4.3