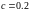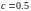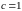- •Глава 1. Оператор Лизеганга
- •Оператор Лизеганга как отражение колебательных свойств гелевых полимерных систем. Введение оператора Лизеганга.
- •1.2.Исследование сильно нелинейного уравнения диффузии
- •1.3. Упрощённая запись оператора Лизеганга
- •Графики для разных значений и . На графике слева приведены значения , справа - . По оси абсцисс отложено время, по оси ординат – значение в безразмерных единицах.
- •График стационарного решения задачи (1.3.5)-(1.3.6). По оси абсцисс отложена безразмерная координата X, по оси ординат – функции и , согласованные при , также в безразмерных единицах.
- •1.5 Оператор Лизеганга и некоторые экспериментальные данные
- •Глава 2 Оптические свойства гелевых оксигидратов и размеры кластеров
- •2.1 Уравнение поглощения света на конформерных “шумовых” кластерах.
- •Концентрационная зависимость кластеров от времени для простейшей спирали.
- •Изменение интенсивности волн прошедшего поля через оксигидратные кластеры в пространстве.
- •2.3 Влияние пульсационного шума или тока самоорганизации в магнитном поле на особенности оптических характеристик окигидрата иттрия.
- •2.4 Кинетические кривые оптической плотности некоторых гелей оксигидратных систем
- •Спектры поглощения силикагелей
- •2.5. Интерферационный подход к экспериментальнолму определению
- •2.6. Вычисления размеров кластеров на примере гелей оксигидрата кремния и иттрия.
- •Зависимости оптической плотности смешанных гелей оксигидрата кремния и оксигидрата иттрия от времени.
- •Глава 3 Каустики стохастических потоковых кластеров и решение задачи формообразования самих кластерных частиц.
- •Глава 4. Каустики лагранжевых отображений гелевой оксигидратной магнитной жидкости железа
- •4.1 Введение
- •4.2 Типичные перестройки каустик в трехмерном пространстве лагранжева многообразия
- •Литература
- •Глава 5 Форма и механизм разряда волновых стохастических кластеров вблизи регистрирующих электродов
- •Результаты и их обсуждение
- •Волновые домены гелей оксигидрата железа,
- •Фазовые портреты двух доменов, указанных стрелками
- •Оксигидрат железа (III)
Глава 3 Каустики стохастических потоковых кластеров и решение задачи формообразования самих кластерных частиц.
В главе 3 проказано, что уравнение движения частиц в геле подчиняется волновому уравнению, поэтому можно применять аппарат нахождения эвольвент для определения волнового фронта в коллоиде оксигидрата железа.
Установлена форма волновых фронтов и, следовательно, границы раздела фаз в коллоиде оксигидрата железа, имеющие форму «амёбы» - неопределённое гелевое гало с рукавами, которые, возможно, имеет самопересечения. Ряд экспериментов [1-4] показывает, что между электродами, помещёнными в коллоиды оксигидратов d- и f- элементов и соединённых между собой через измерительный прибор (рис. 1), возникает небольшая разность потенциалов (примерно 0.2 Вольта) и небольшой электроток, имеющий прерывистый характер, аиплитудой от нескольких наноампер до микроампера (рис. 3.2). Это установлено нами в большом количестве публикаций (например, [1-4]).
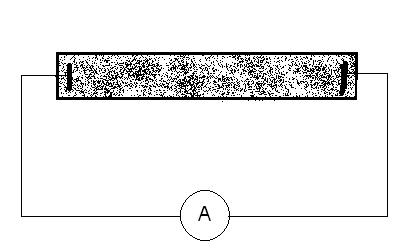
Рис. 3.1.
Принципиальный рисунок электрической цепи для регистрации токовых всплесков. В цепь включён амперметр, в пробирку, закрашенную серым цветом, помещены электроды. Площадь электродов составляет примерно 1 квадратный сантиметр, оба электрода угольные.
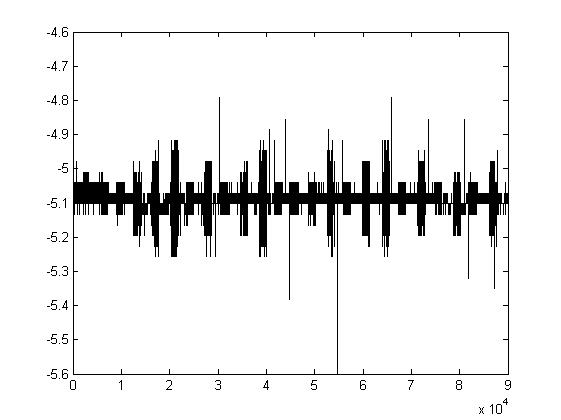
Рис.3. 2.
Токовые колебания во времени. Один из экспериментов на геле оксигидрата железа (III).
На рисунке отчётливо видны сильные всплески тока, не укладывающиеся в статистику.
Можно ли дать объяснение этому току как статистическому явлению, как колебанию плотности свободных зарядов в коллоиде? Вне всякого сомнения, часть этого тока, действительно, является колебанием свободных зарядов. Однако, как нам представляется, все намного сложнее [2, 3]. На рис.3. 2; 3.3 присутствует некая компонента кластерного потока, которая не может быть объяснена только статистически. Дело в том, что статистические флуктуации подчиняются нормальному распределению, которые имеют некоторое среднее. Если же возникают флуктуации ионных потоков (зарядов), располагающихся далеко от среднего, то такие флуктуации должны быть маловероятными.
Тем
не менее, экспериментально видно, что
достаточно часто наблюдаются всплески
тока, которые отстоят от среднего дальше,
чем на 9 и больше средних квадратических
отклонений. Вероятность такого отклонения
должна составлять
 ,
и такой результат, конечно, хотя и может
наблюдаться в 100000 измерений, но крайне
маловероятен, чтобы повториться.
Экспериментально такие скачки все-таки
наблюдаются, примерно один на 15000
измерений, то есть в одной серии из
100000 измерений повторяются 6 и более раз.
А это означает, что такое событие
объяснить только статистически
практически невозможно. Следовательно,
по крайней мере, часть колебаний нельзя
рассматривать как случайную величину.
,
и такой результат, конечно, хотя и может
наблюдаться в 100000 измерений, но крайне
маловероятен, чтобы повториться.
Экспериментально такие скачки все-таки
наблюдаются, примерно один на 15000
измерений, то есть в одной серии из
100000 измерений повторяются 6 и более раз.
А это означает, что такое событие
объяснить только статистически
практически невозможно. Следовательно,
по крайней мере, часть колебаний нельзя
рассматривать как случайную величину.
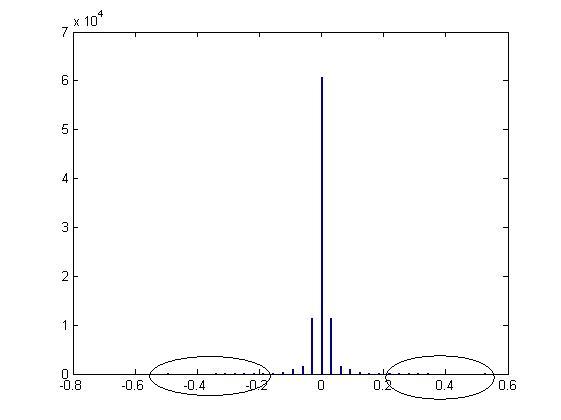
Рис. 3.3.
Колебания
тока
 для опыта, соответствующие рис. 3. 2.
для опыта, соответствующие рис. 3. 2.
Кружками обведены величины, которые нельзя рассматривать как случайные.
Попробуем дать иную интерпретацию возникновения ионных потоков, нежели только как статистическую (или случайную).
Химические реакции и их уравнения.
Коллоидные фрагменты являются нестабильными и постоянно трансформируются как физически, так и химически. Можно сказать, что между различными вещественными элементами, составляющими коллоид, наблюдаются химические реакции.
В наших работах ранее показано [5], что для коллоидных кластерных систем бичастичные взаимодействия не характерны, запрещены [12]. При этом обязательно должна появиться (образоваться) третья частица (как правило, легкоподвижная), которая диссипирует (размазывает) энергию по объему системы структурно определенным образом, тем самым делая эту структурную организацию энергетически выгодной.
Эти частицы формируются и в процессе деструкции бидендатно взаимодействующих макромолекул оксигидратной матрицы. Макромолекулы при этом могут практически даже соприкосаться. Механизм формирования третьих кластеров заключается в диссоциативно-диспропорциональном разрушении макромолекул оксигидратного геля, а также их двойных электрических слоев (ДЭС). Так как при этом образуются относительно небольшие заряженные “осколочные” кластеры, то они способны перемещаться в пространстве дисперсионной среды по определенным линиям тока скачкообразно в узкой пристеночной к электроду области, определяемой длиной диффузионного перескока или области “взаимодействия” [2, 3], которые задаются в системе некими стохастическими потенциалами, например, ретчет-потенциалами. Скорости диссоциативно-диспропорционального состояния определяются соответствующими константами реакции, например, Аррениуса.
Например,
пусть идёт превращение вещества
 в вещество
в вещество
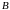 ,
которое тут же распадается с формированием
вещества
,
которое тут же распадается с формированием
вещества
 .
Тогда характеристикой вещества
в данной точке пространства будет его
концентрация
.
Тогда характеристикой вещества
в данной точке пространства будет его
концентрация
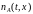 в данной точке
в данной точке
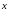 (мы будем считать сумму веществ
(мы будем считать сумму веществ
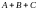 как
непрерывную среду, пренебрегая размерными
масштабами компонентов, например,
молекулярно нанокластерными).
Соответственно, характеристикой вещества
будет его концентрация
как
непрерывную среду, пренебрегая размерными
масштабами компонентов, например,
молекулярно нанокластерными).
Соответственно, характеристикой вещества
будет его концентрация
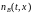 .
.
Химическую
реакцию можно изобразить с помощью
фазового портрета на плоскости
концентраций (т.е. на такой плоскости,
где по осям отложены концентрации
реагирующих веществ). Например, если
реакция между веществами
и
диссоциативно обратима, то фазовая
траектория превращений может быть
окружностью (см. рис. 3.4), при этом надо
иметь в виду, что нанокластер
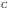 нормально
разряжается на графитовой поверхности.
Все это, естественно, происходит в
условиях далеких от равновесных.
нормально
разряжается на графитовой поверхности.
Все это, естественно, происходит в
условиях далеких от равновесных.

Рис. 3.4.
Фазовая диаграмма простой обратимой реакции. По осям координат отмечены концентрации веществ.
Таким
образом, для данной пространственной
точки можно записать уравнение для
концентраций: ,
и это уравнение будет связывать
концентрации двух этих веществ в любой
момент времени в данной точке, естественно
в условиях далеких от равновесия.
,
и это уравнение будет связывать
концентрации двух этих веществ в любой
момент времени в данной точке, естественно
в условиях далеких от равновесия.
Электрические
токи и химические реакции.
Теперь отметим, что концентрации и токи
связаны соотношением
 ,
где
,
где
 - коэффициент, определяемый веществом.
Следовательно, ионный поток, который
может возникнуть при кластерном
перемещении зарядов, определяется
формулой
- коэффициент, определяемый веществом.
Следовательно, ионный поток, который
может возникнуть при кластерном
перемещении зарядов, определяется
формулой
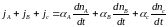 .
.
Вид
кривой электрического тока, определяемый
химической реакцией, можно определить
по-разному, в зависимости от коэффициентов
скорости (или констант скорости),
соответствующих данным кластерам. В
случае нашего примера, когда
,
можно ввести фазу
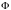 ,
которая будет связана с
,
которая будет связана с
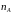 и
и
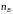 соотношением
соотношением
 ,
,
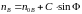 .
Отсюда следует выражение для тока:
.
Отсюда следует выражение для тока:
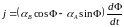 .
.
В
общем случае можно описать уравнение
следующим образом: пусть
- некая координата вдоль линии на фазовой
плоскости, которая является координатой
вдоль фазовой кривой реакции, своего
рода – фаза реакции. Тогда концентрации
 реагирующих веществ связаны с фазой
соотношениями
реагирующих веществ связаны с фазой
соотношениями
 ,
а ток, создаваемый перемещающимся
кластером, записывается как
,
а ток, создаваемый перемещающимся
кластером, записывается как
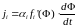 .
При этом общий ток может быть определён
формулой
.
При этом общий ток может быть определён
формулой
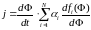 .
Здесь неявно учтен третий компонент
.
.
Здесь неявно учтен третий компонент
.
Следовательно,
проинтегрировав уравнение по току,
получим линейное соотношение для
некоторой суммы фаз кластеров:
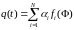 .
.
Таким образом, появляется средство, которое позволяет делать определённые выводы о химических процессах – при условии, что мы знаем, что связывает концентрацию кластеров с их собственным ионным потоком в условиях неравновесия (т.е. электрическим нанотоком, создаваемым в коллоидном геле оксигидрата в ячейке, рис.3.1).
Каустики. Для формирования топологической геометрии каустики этот третий компонент является определяющим. В действительности на практике отмечаются скачки токов. Если мы предполагаем, что ток обусловлен постоянным изменением концентрации, то кривая будет плавной только в том случае, если фазы везде одинаковы или одинаково меняются. Если же в разных точках пространства химические реакции идут различно и/или находятся в разных фазах, то масса вещества (кластеров) будет представлять собой источник волновых потоков (гелевых волн) [1] . Поток заряженных кластеров в этом случае можно сопоставить с лучом, который огибает некоторую фазовую поверхность. Заметим, что эта линия (линии) является геометрической, пространственной, и её уместно назвать «эквифазовой поверхностью».
Это сопоставление уместно при условии, если отсутствует плавный переход между фазами. Тогда поток частиц, если между фазами существует разность потенциалов, будет перпендикулярен эквифазовой поверхности, а точки, где эти лучи, образующие гелевую волну, будут интерферировать. При этом будут складываться каустики, огибающие потоки заряженных частиц.
Мы считаем, что наиболее сильные всплески тока соответствуют интерференции (или простому сложению) потоков заряженных частиц, идущих от разных эквифазовых поверхностей. Простейшая практическая польза, которую можно извлечь из этого наблюдения – период химической реакции. Его можно замерить как промежуток времени между наиболее крупными всплесками. Скажем, на рис. 3.2 можно отметить 7 или 8 крупных всплесков. Так как общее время замеров составляет 6 часов, то период химической реакции составляет примерно 40-45 минут.
Отметим, что волновые гелевые каустики в принципе открывают чрезвычайно большие возможности для исследований геометрических форм поверхностей раздела фаз.
Однако необходимо знать, как именно ведут себя потоки частиц на поверхности раздела: просто ли они отражаются, подобно лучам света на зеркальной поверхности или же, наоборот, просто проходят внутрь, слегка преломляясь. Кроме этого, поверхность электрода позволяет регистрировать потоки, которые на неё попали, играя роль плоскости сечения Пуанкаре в пространстве, но при этом она не показывает, где именно, в какой пространственной точке располагается каустика, она показывает только момент обнаружения каустики.
Исходя из химических реакций, происходящих в коллоиде, мы можем полагать, что потоки порождаются малыми частицами (кластерами), отщепляющимися или вновь присоединяющимися к гелевым фрагментам.
Построим априори модель движения этих частиц. Частицы движутся в поле стохастического ретчет-потенциала [1,6], создаваемого средой, то есть крупными малоподвижными молекулами и самыми малыми частицами (нанокластерами) [2, 3]. Движению (возможно, даже просто смещению) частиц можно сопоставить волновые фронты, так как вне взаимодействия движение частиц прямолинейно.
При наложении волновых фронтов будет увеличиваться количество частиц в узкой области приэлектродного пространства (то есть в условиях далеких от равновесия). Такому явлению представляется уместным поставить в соответствие своеобразную гелевую каустику – область, где наблюдается, в силу пересечения потоков движения частиц (или их интерференции), их скопление. Аналог оптической интерференции, на наш взгляд, здесь не уместен, так как потоки кластеров могут быть и не когерентными – например, может быть достаточно большая разность хода волновых фронтов. В данном случае следует говорит о гелевой или коллоидной дифракция (интерференции) в условиях, далеких от равновесия [6, 7].
При данном неупругом взаимодействии частиц-кластеров образуются своеобразные ударные волны, подчиняющиеся нелинейному уравнению Бюргерса. Считая ударные волны волнами бегущими, можно использовать аппарат, развитый для волновых уравнений, в частности, формулы, позволяющие работать с каустиками [8, 9].
Эвольвенты кластерных потоков. Экспериментально обнаружены движения коллоидных кластеров как колебания нанопотоков, рис.3.3 [4]. Их двухмерные фазовые диаграммы (каустики), построенные на небольших задержках, имеют довольно своеобразные формы, для которых есть соблазн объявить их аналогами оптических каустик, широко известными и широко используемыми для разных целей.
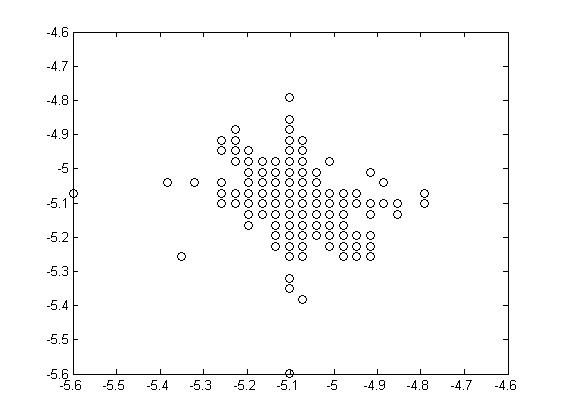
Рис.3.5.
Фазовая диаграмма тока. По осям отложены значения тока:
по
оси абсцисс
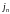 (ток в момент времени
),
(ток в момент времени
),
по
оси ординат ток
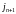 (ток в момент времени
(ток в момент времени
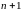 ).
).
Отметим, что наша задача состоит в том, чтобы, зная двумерную фазовую каустику, восстановить форму «зеркала», то есть границы раздела фаз, или форму изначальных кластерных частиц.
Так как мы используем аппарат рассмотрения экспериментальных данных (рис.3.3) в форме волнового уравнения, то волновой фронт (а, следовательно, и сама граница раздела фаз) располагается на одной из возможных эвольвент двумерной каустики [8,9]. Следовательно, наша задача состоит в нахождении эвольвенты кривой, где эволюта - известная граница гелевой каустики [10,11].
Отметим, что само уравнение границы двумерной каустики неизвестно и его необходимо находить.
Нас интересует, по сути дела, вопрос о восстановлении формы границы раздела фаз. Для этого можно отметить, что если считать токовую каустику первого возвращения исходной кривой, то волновой фронт будет её, каустики, эвольвентой (инволютой).
Ограничимся построением волнового фронта по известной каустике фазового пространства. Для этого воспользуемся результатами [10].
Эвольвента кривой может быть построена по следующим формулам [11]:
 (3.1)
(3.1)
где
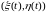 - точка на эволюте (в нашем случае это
фазовая каустика),
- точка на эволюте (в нашем случае это
фазовая каустика),
 - выбранный нами параметр, мы можем
выбрать его произвольно,
- выбранный нами параметр, мы можем
выбрать его произвольно,
 - параметр на фазовой каустике,
- параметр на фазовой каустике,
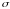 - длина пройденной кривой (в [11] прямая,
с помощью которой строится эвольвента,
скользит по фазовой каустике),
- длина пройденной кривой (в [11] прямая,
с помощью которой строится эвольвента,
скользит по фазовой каустике),
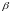 - угол, который скользящая прямая образует
с положительным направлением оси
абсцисс.
- угол, который скользящая прямая образует
с положительным направлением оси
абсцисс.
Способ вычислений. Отметим, что непосредственно формулой (1) пользоваться неудобно, так как на фазовой диаграмме точки расположены очень сложным образом, угол касательной меняется очень резко, и поэтому необходимо определённое сглаживание исходной фигуры, в противном случае мы получим набор хаотически расположенных точек, которые будут иметь очень мало общего с исходной фигурой.
Это означает, что мы должны будем ввести дополнительное предположение о гладкости полученной фигуры. Также мы будем считать, что все внутренние точки фазовой каустики не имеют отношения к волновому фронту и обусловлены явлениями, лежащими где-то внутри области. Таким образом, мы будем считать, что между границей фазовой каустики и границей раздела фаз существует взаимно-однозначное соответствие: все точки границы фазовой каустики однозначно соответствуют точкам волнового фронта раздела фаз. Это предположение существенно осложняется тем, что мы предполагаем фрактальный характер среды – в этом случае довольно сложно говорить о волновом фронте. Тем не менее, считая, что таким образом, можно получить «сглаженную» линию, попытаемся провести восстановление волнового фронта.
Будем
считать, что каустика, построенная нами,
может быть задана полярным уравнением
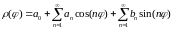 ,
т.е. полярный радиус
,
т.е. полярный радиус
 может быть представлен в виде специфического
ряда Фурье – ряда, сумма которого
неотрицательна при всех значениях
полярного угла
может быть представлен в виде специфического
ряда Фурье – ряда, сумма которого
неотрицательна при всех значениях
полярного угла
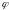 .
Тогда коэффициенты этого ряда можно
найти с помощью обычных формул ряда
Фурье [2]:
.
Тогда коэффициенты этого ряда можно
найти с помощью обычных формул ряда
Фурье [2]:
 ,
,
 ,
,
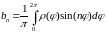 .
.
Эти формулы также являются и среднеквадратичным приближением.
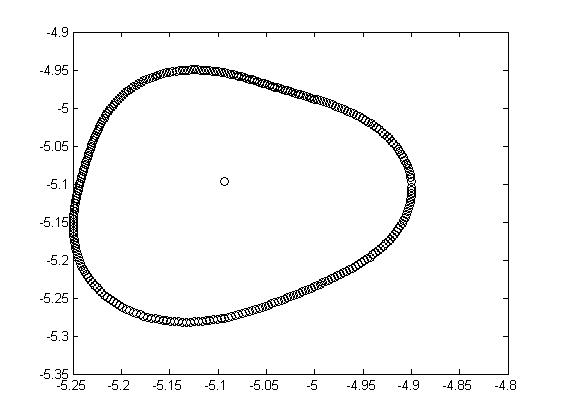
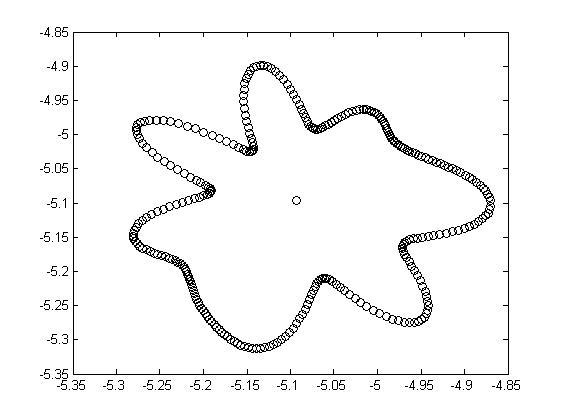
Рис.3.6.
Приближение исходной кривой с помощью Фурье-гармоник.
Слева – 4 гармоники, средний и правый соответственно 10 и 20 членов ряда Фурье.
Заметим, что приближение достаточно неточное. Это связано с возможной неодносвязностью исходной фазовой каустики (рис. 3.5), хаотическим характером точек.
Заметим, что задача восстановления гладкой границы области имеет и чисто математические сложности: во-первых, не понятно, односвязна ли сама аттракторная область каустики? Во-вторых, затруднения в стандартных математических методах вызывает вопрос о принципиально-негладком характере фронта, его хаотичности. В результате метод расчета даёт достаточно приближенный результат (см. рис. 7), в то время, как из рисунка 6 следует, что наращивание числа гармоник не приведёт к улучшению точности – ошибка может быть обусловлена указанными выше трудностями.
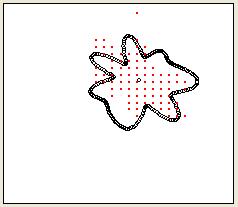
Рис. 3.7
Точность нахождения границы. Красные точки на рисунке – положение точек фазовой каустики (рис.3.2).
Чёрные точки – граница, найденная разложением в ряд Фурье.
Неточность носит принципиальный характер: из вида фазовой каустики не очевидна её граница. Предполагаемая нами граница носит достаточно формальный характер. К тому же, она сильно сглажена – для неё написано разложение в ряды Фурье.
Эвольвенты. Вычисления эвольвенты по формулам (1) для разных значений параметра приведены ниже. В качестве границы мы брали значения, полученные при 20 членах ряда (21 коэффициент ряда косинусов и 20 ряда синусов, всего 41 число).
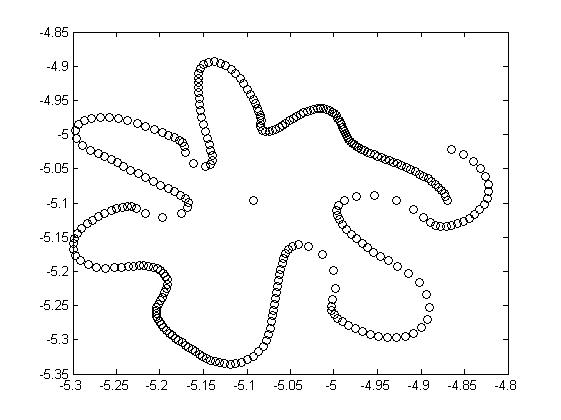
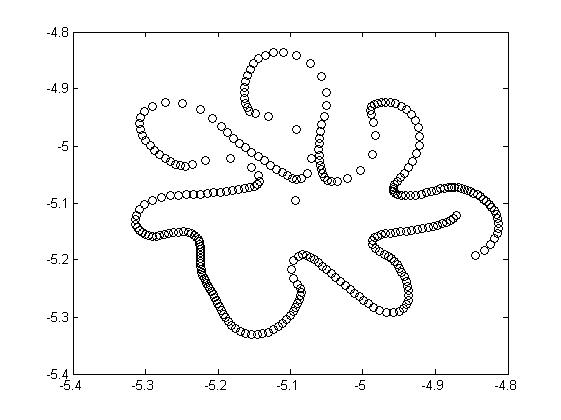
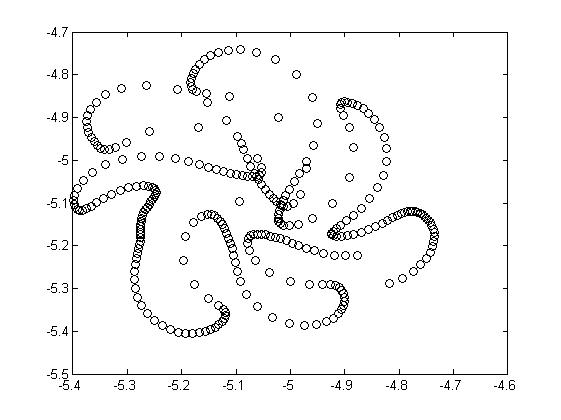
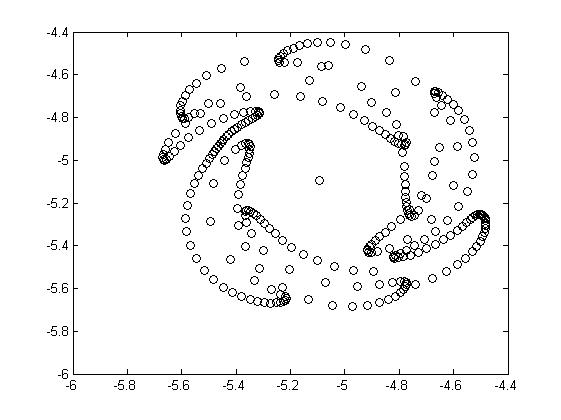
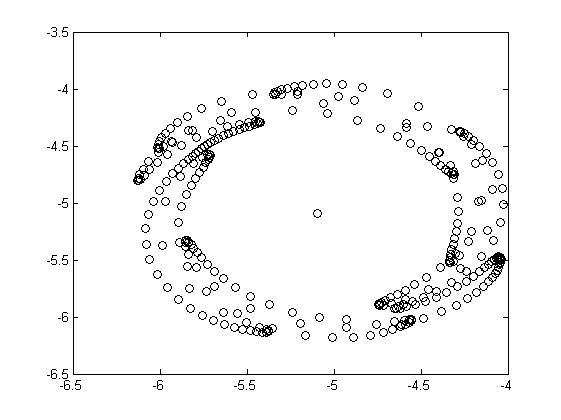
Вид эвольвент для одной фазовой каустики и разных значениях параметра (расстояния до волнового фронта) приведён на рис. 3.8.
|
|
|
|
|
|
Рис.3.8. Восстановленные волновые фронты для различных значений параметра (на разных удалениях от каустики) |
|
Из рисунка видно, что по мере отдаления от каустики в фазовом пространстве волновой фронт принимает всё больше форму круга, а вихревые структуры, образующие границу фронта, всё больше смешиваются. Из этого следует, что граница раздела фаз имеет сложную структуру. Предположительно она имеет вид, соответствующий рисунку, соответствующему - система сложных рукавов, имеющих ряд самопересечений.
Итак, мы получили форму волновых фронтов и, следовательно, границы раздела фаз в коллоиде оксигидрата железа, имеющие форму «амёбы» - неопределённого гелевого гало с рукавами, которые, возможно, имеют самопересечения. Однако эта форма близка сфероидальным гелевым частицам оксигидратных коллоидов, на которых удивительным образом отображаются особенности Уитни [8, 9], применительно к особым точкам на складке фазовой каустики, так как на поверхности рассчитанного кластера отмечаются некие активные зоны, в которых идет стохастическое диссоциативно-диспропорциональное выталкивание в дисперсионную среду гидратированных ионных кластерных образований оксигидрата, связанное с разрушением слоев Гуи-Штерна, рис. 3.8.
Однако для установления точной формы границ раздела фаз необходимы дальнейшие исследования.
Выводы.
1. Уравнение движения частиц в геле подчиняется волновому уравнению, поэтому можно применять аппарат нахождения эвольвент для определения волнового фронта в коллоиде оксигидрата железа (III),
2. Получена форма волновых фронтов и, следовательно, границы раздела фаз в коллоиде оксигидрата железа, имеющих форму «амёбы» - неопределённого гелевого гало с рукавами, на котором отображаются особенности Уитни.
3. Фазовая каустика определяет форму пространственной каустики, на которой видны некие химически-активные зоны, или особенности Уитни.
Цитируемая литература.
Yuri I. Sucharev. Wave Oscillations in Colloid Oxyhydrates // Switzerland, UK, USA: Trans Tech Publications LTD. 2010. 497 p.
Yuri I. Sucharev. Nonlinearity of Colloid Systems: Oxyhydrate Systems // Switzerland, UK, USA: Trans Tech Publications. 2007. 433 p.
Сухарев Ю.И., Пролубникова Т.И., Лебедева И.Ю. и Апаликова И.Ю. Отображение периодических изменений «шумовых» вязкостных характеристик гелевых оксигидратных систем // Бутлеровские сообщения. 2010. Т.19. №1. С.44-54.
Y.I. Sucharev, B.A. Markov, I.Y. Lebedeva, T.I. Prolubnikova “Quasi-periodic noise oscillations in oxyhydrates of rare-earth elements” // Eurasian Chemical-Technological journal, vol. 14, № 1, 2012, P. 61-72.
Сухарев Ю. И., Крутикова О. М., Азаров М. Б., Пролубникова Т. И. «Пространственая организация гигантских кластеров бидистиллированной и деионизированной естественной воды» // Бутлеровские сообщения. 2011. Т.28. №18. С.11-32.
Анищенко В.С., Астахов В.В., Вадивасова Т.Е. и др. Нелинейные эффекты в хаотических и стохастических системах. Москва-Ижевск: Институт компьютерных исследований.2003. – 529 с.
Шемякин Ф.М, Михалёв П.Ф. «Физико-химические периодические процессы». Изд-во АН СССР, 1938. С. 138.
Арнольд В.И. Теория катастроф. -М.: Едиториал УРСС, 2004.- C. 128.
Арнольд В. И. Особенности каустик и волновых фронтов. М.: Фазис, 1996. С. 562.
Фихтенгольц Г.М. «Курс дифференциального и интегрального исчисления», том 1, М.: ФМЛ, 1962.- 608 с.
Фихтенгольц Г.М. «Курс дифференциального и интегрального исчисления», том 3, М.: ФМЛ, 1969.- 656 с.
Суздалев И. П. Нанотехнология: Физико-химия нанокластеров и наноматериалов.-2-е изд., испр. - М.: URSS, 2008. – 589 с.