2.5. Интерферационный подход к экспериментальнолму определению

средних размеров ионных кластеров оксигидраьных гелей d- и f- элементов

Законы поглощения.

В турбидиметрических измерениях обычно принимается во внимание только поглощение света. Считается, что поглощение пропорционально концентрации, и интенсивность на входе и выходе 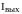связаны соотношением: , где - концентрация вещества, - длина кюветы, - коэффициент пропорциональности, определяющий поглощение излучения единицей концентрации на единицу длины, пройденной излучением в веществе [30].

Если коэффициент известен, то несложно найти концентрацию (закон Бугера-Ламберта-Бера): .

Однако в наших экспериментах получается, что концентрация в кювете периодически (самопроизвольно) изменяется, хотя этого вроде бы не должно быть: количество вещества в кювете остаётся неизменным, в ходе измерений ничего не убавляется и ничего не исчезает. Остаётся только предположить, что вещество как-то перераспределяется. Однако этот подход имеет определённые трудности для математической интерпретации.

Действительно, пусть поглощение происходит различно в кластерах и межмицеллярной жидкости. Пусть по ходу света вся длина кюветы , из неё кластеры занимают 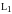, а межмицеллярная жидкость . Тогда верно, что . Пусть в кластерах поглощение , а в дисперсионной среде поглощение 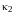. В результате мы для разного распределения концентраций получим две разные формулы:

- для набора концентраций - концентрация поглощающего вещества в кластерах, - концентрация поглощающего вещества в дисперсионной среде. - Для другого набора размеров кюветы и концентраций.

В результате для определения неизвестных нам величин мы получим систему уравнений:

Таким образом, на восемь неизвестных величин , , , , , , , есть система из всего лишь пяти уравнений. Даже если предположить, что нам известны величины - коэффициенты поглощения, то одна величина остаётся неизвестной. Её можно найти, если вычислить повременное распределение кластеров, либо использовать иные коллоидно-химические ухищрения. В любом случае мы сможем решить систему полученных обыкновенных уравнений.

Заметим, что если считать поглощение света как в кластерах, так и в межмицеллярной жидкости одинаковым, то предложенная система уравнений бессмысленна, и различить поглощение невозможно – или требуются дополнительные измерения и предположения.

В целом решение системы уравнений представляется очень заманчивым: мы можем сразу получить большое количество информации о коллоидной системе: найти соотношение концентраций в кластерах и в межмицеллярной жидкости, соотношение длин и т.д. В принципе, даже можно попытаться определить соотношение поглощения между мицеллярной жидкостью и дисперсиогной средой.

Кроме того, система допускает существенное расширение за счёт иных разумных предположений. В принципе возможно объединение этого уравнения с системой уравнений Лизеганга и решать совместно эти уравнения. При этом можно попытаться определить огромное число экспериментальных характеристик, как-то: периоды и петли оператора Лизеганга коллоидной системы, ряд и других ее параметров. Всё дело в том, как именно все это решать математически – информации же у нас более чем достаточно.

Всё зависит лишь от того, насколько достоверно можно опираться на закон поглощения, то есть насколько “грубые оценки” дает этот метод. Если он достаточно точен, то явно стоит попробовать это сделать.

Дифракция на оксигидратных кластерах.

В работе [31] нами показано, что при определенных размерах оксигидратных кластеров видимый свет уже не просто поглощается гелевой фазой, а начинает интерферировать. Это и позволило нам разработать экспериментальный способ (достаточно громоздкий и не очень точный) оценивания размеров оксигидратных кластеров. Теперь попытаемся рассмотреть другой подход, связанный с дифракцией на гелевых кластерах. То есть это развитие идей, рассмотренных в [31].

Представим себе, что свет падает на скопление частиц, которые меняют свой размер вследствие каких-то причин. Частично свет поглощается, частично – дифрагирует, если размеры этих частиц соизмеримы с размерами волны света.

Так как количество вещества остаётся неизменным, то можно предположить, что поглощение меняется мало; это будет соответствовать тому, что , - или же поглощение меняется мало в зависимости от концентрации.

Пусть на каждом из фрагментов идёт дифракция (рис. 2.15).

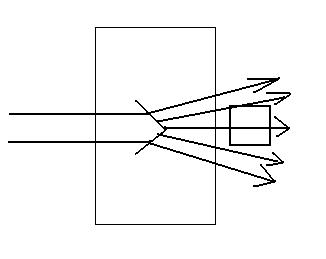
Рис.2.15

Схематическое представление дифракции-рассеяния в веществе.

Тогда интенсивность будет связана с интенсивностью парциальной (т.е. интенсивностью, распределившейся в определённый полярный или телесный угол) как , где - полярный угол, где - размер препятствия [30], - длина волны света, - нормирующий множитель, включающий в себя как поглощение, так и нормировку. Если поглощения нет, то он будет равен единице, делённой на интеграл по всем допустимым углам рассеяния (если меняется от до , то 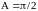). Тогда, если учитывать, что мы способны зафиксировать лишь свет, падающий на сенсор, имеющий окошко радиуса , то интегрировать функцию дифракции будем в пределах от 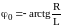до , где - длина кюветы. В результате получим формулу:

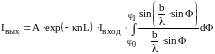
или . Вид функции 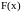приведён ниже, на рис. 2.16

.

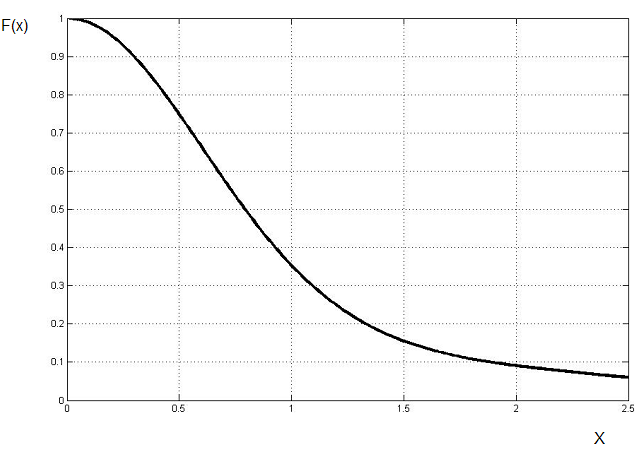
Рис. 2.16

Вид функции - для безразмерного параметра , отложенного по оси абсцисс. Заметим, что величина , и если , то кластер в 10 раз меньше волны света, а если 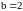, а , то кластер вдвое больше световой волны. Сама функция отложена по ос ординат и не имеет размерности – просто число.

Сравнивая максимальное измеренное выходное значение 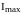с минимальным измеренным выходным значением , можно исключить поглощение:

Это соотношение содержит две неизвестных величины: и . Поэтому необходимо выявить, при каких значениях параметров наблюдается наибольшее отношение . Для этого удобно воспользоваться рис.2.17 .

На рис.2.17. указано отношение для разных . Самая нижняя линия - , выше – 0.2 и т.д.

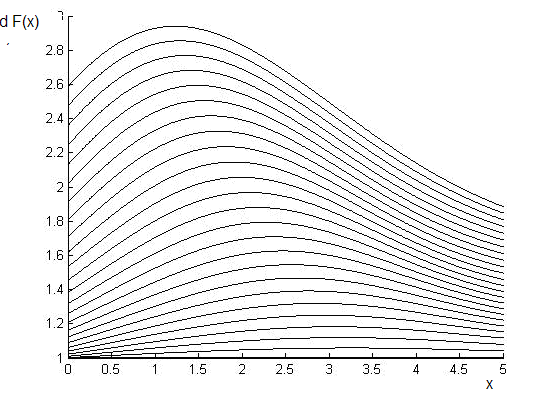
Рис.2.17 .

Семейство функций для разных в зависимости от переменной .

Как им пользоваться? Введём симплекс . Выберем наибольшее значение величины , которая будет наблюдаться при определённой длине волны .

Сопоставим это соотношение с разными графиками . Тот из них, который будет менее всего отличаться от экспериментального графика (менее всего – например, в смысле метода наименьших квадратов), и будет соответствовать реальному .

Итак, величину мы, таким образом, можем найти. Заметим, что максимуму этого графика будет соответствовать некая величина , которую мы определим по виду графика 2.17. Следовательно, мы можем указать , и . Из этих соотношений, зная длину волны света, найдём наибольшее и наименьшее значение кластера: , , .

Функция имеет единственный глобальный максимум. Обозначим его положение на графике функции как , т.к. его положение зависит от параметра , рис.2.17

Поставим этой точке максимума в соответствие экспериментально обнаруженное отношение , т.е. будем считать, что отношение соответствует положению максимума графика функции . Заметим, что это соответствует смыслу функции . Зная величину и зная величину максимума , мы можем определить значение и величину . Для этого воспользуемся графиком на рис.2.18

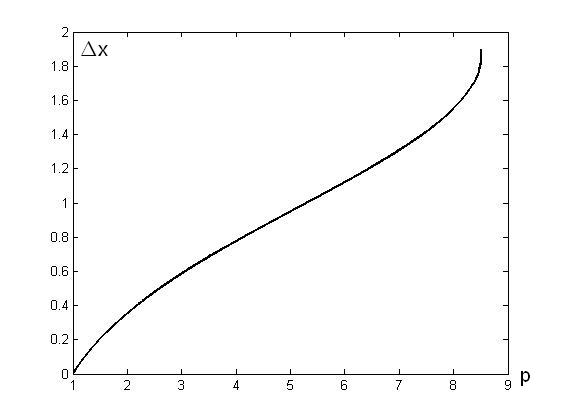
Рис.2.18

График зависимости параметра от величины максимума функции. По оси абсцисс – отношение наибольшей к наименьшей интенсивности, по оси ординат – значение .

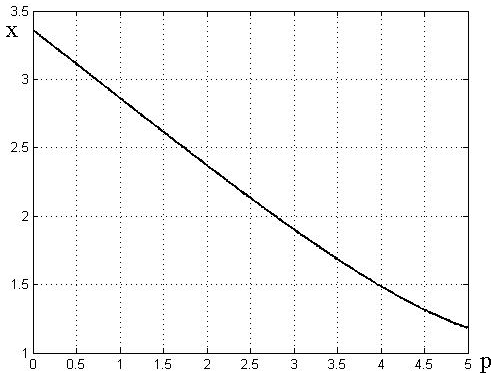
Рис.2.19

График зависимости параметра от величины максимума симплепкса р .

По оси абсцисс отложено отношение наибольшей к наименьшей интенсивности , по оси ординат – значение .

Итак, пусть значение 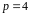. Откладываем его по оси абсцисс графика рис.2.18 а по оси ординат получаем соответствующее ему значение , равное примерно 0.7

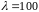Теперь воспользуемся графиком 2.19 чтобы определить значение , соответствующее величине данного максимума. Оно равно примерно 1.5. Таким образом, мы получили отношение наибольшего и наименьшего размеров к длине волны, т.е. , . Пусть нм, тогда наибольший размер получается равным 220 нм, а наименьший – 150 нм. Следовательно, кластер меняет свой размер от 150 нм до 220 нм.