1.5.2 Опоры и опорные реакции балок

Правило для определения направления реакций связей ( рис.1.22).

Шарнирно-подвижная опора допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плос­кости. Если пренебречь трением на опоре и в шарнире, то реак­ция такой связи будет направлена перпендикулярно опорной плоскости и неизвестна только по модулю (одно неизвестное).

Шарнирно-неподвижная опора допускает только поворот вокруг оси шарнира и не допускает никаких линейных переме­щений. Реакция такой опоры будет направлена перпендикуляр­но оси шарнира; модуль и направление ее заранее неизвестны (два неизвестных). Обычно при решении задач такую реакцию раскладывают на две взаимно перпендикулярные составляющие, неизвестные по модулю, но известные по направлению.

Жесткая заделка (защемление) не допускает ни линейных перемещений, ни поворотов защемленного конца балки. Жест­кую заделку заменяют реактивной силой, неизвестной по моду­лю и направлению, и реактивным моментом (три неизвестных). Реактивную силу, неизвестную по направлению, раскладывают на две взаимно перпендикулярные составляющие.

Е сли при решении задачи реактивная сила или реактивный момент получатся отрицательными, то их действительное на­правление противоположно принятому на рисунке.

Кроме перечисленных выше трех основных типов опор ба­лок, в конструкциях нередко балка свободно опирается на плос­кость (поверхность) или на ребро призмы. В этих случаях направление реакций определяют по правилам, изложенных заранее. рис.1.22

Тема 1.6 Плоская система произвольно расположенных сил

Иметь представление о главном векторе, главном моменте, равнодействующей плоской системы произвольно расположенных сил.

Знать теорему Пуансо о проведении силы к точке, приведение произвольной плоской системы сил к точке, три формы уравнений равновесия.

Уметь заменять произвольную плоскую систему сил одной силой и одной парой.

Приведение силы к точке.

Произвольная плоская система сил представляет собой систему сил, линии действия которых расположены в плоскости каким угодно образом (рис. 1.23).

Возьмем силу , приложенную в точке С. Требуется пере­нести эту силу параллельно самой себе в некоторую точку О.

П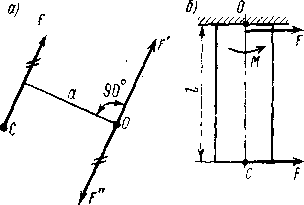 риложим в точке О две силы и , противоположно направленные, равные по значению и параллельные заданной силе , т. е. F' = F" = F. От приложения в точке О этих сил состояние тела не изменяется, так как они взаимно уравновешиваются. Полученную систему трех сил можно рассматривать как состоящую из силы , приложенной в точке О, и пары сил с моментом М = Fa. Эту пару сил называют присоединенной, а ее плечо а равно плечу силы относительно точки О (рис. 1.23, а).

Таким образом, при приведении силы к точке, не лежащей на линии действия силы, получается эквивалентная система, состоящая из силы, такой же по модулю и направлению, как и сила , и присоединенной па­ры сил, момент которой равен моменту данной силы относи­тельно точки приведения (Теорема Пуансо):

М₀ ( ) = Fa. Рис.1.23

Приведение плоской системы сил к данной точке

М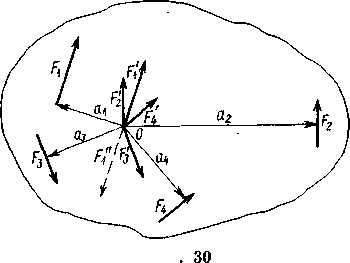 етод приведения одной силы к данной точке можно применить к какому угодно числу сил. Допустим, что в некото­рых точках тела (рис. 1.24) приложены силы F₁ F₂, F₃ и F₄. Тре­буется привести эти силы к точке О плоскости. Приведем сначала силу приложенную в точ­ке А. Приложим (см. § 16) в точке О две силы рав­ные порознь по значению заданной силе параллель­ные ей и направленные в про­тивоположные стороны. В ре­зультате приведения силы получим силу , приложен­ную в точке О, и пару сил с плечом . Поступив таким же образом с силой , приложенной в точке В, получим силу , приложенную в точке О, и пару сил с плечом и т. д. Плоскую систему сил, приложенных в точках А, В, С и D, мы заменили сходящимися силами , приложенными в точке О, и парами сил с моментами, равными моментам заданных сил относительно точки О:

рис.1.24

.

Сходящиеся в точке силы можно заменить одной силой равной геометрической сумме составляющих,

Эту силу, равную геометрической сумме заданных сил, называют главным вектором системы сил и обозначают .

По величине проекций главного вектора на оси координат находим модуль главного вектора:

На основании правила сложения пар сил их можно заменить результирующей парой, момент которой равен алгебраической сумме моментов заданных сил относительно точки О и называется главным моментом относительно точки приведения

Таким образом, произвольная плоская система сил приводиться к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).

Необходимо усвоить, сто главный вектор не является равнодействующей данной системы сил, так как эта система не эквивалентна одной силе . Так как главный вектор равен геометрической сумме сил заданной системе, то ни модуль, ни направление его не зависит от выбора центра приведения. Значение и знак главного момента зависит от положения центра приведения, так как плечи составляющих пар зависят от взаимного положения сил и точки (центра) относительно которой берутся моменты.

Частные случаи приведения системы сил:

1) ; система находиться в равновесии, т.е. для равновесия плоской системы сил необходимо и достаточно, чтобы ее главный вектор и главный момент одновременно были равны нулю.

2) тело вращается вокруг неподвижной оси ;система приводиться к паре сил, момент которой равен главному моменту.

3) тело движется прямолинейно ускоренно; система приводиться к одной равнодействующей, равной главному вектору системы.

4) - общий случай; система приводиться к главному вектору и к главному моменту.

Влияние точки приведения

Точка приведения выбрана произвольно. Произвольная плоская система сил представляет собой систему сил, линия действия которых расположены в плоскости каким угодно образом.

При изменении положения точки приведения величина главного вектора не измениться.

Величина главного момента при переносе точки приведения измениться, т.к. меняются расстояния от векторов - сил до новой точки приведения.

Для того чтобы оказываемое ею на тело действие не изменилось, нужно к нему приложить пару с моментом, равным моменту исходной силы относительно точки, в которую она переноситься.

В общем случае, когда , всегда есть точка, относительно которой главный момент сил равен нулю.

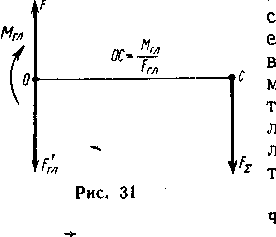Рассмотрим плоскую систему сил, которая приведена к точке О, т. е. заменена главным вектором , приложенным в точке О, и главным моментом (рис. 31). Для определенности примем, что главный момент направлен по часовой стрелке, т. е. М_гл > 0. Изобразим этот главный момент парой сил , модуль которых выберем равным модулю главного вектора. Одну из сил, составляющих пару (силу "). приложим в центре приведения О, другую силу в точке С, положение которой определится из условия: М_гл = OCF_x. Сле­довательно

ОС = M_гл /F_гл, т.е. рис.1.25

где d – расстояние от выбранной точки приведения до точки приложения равнодействующей;

-величина главного момента относительно выбранной точки приведения;

- величина главного вектора системы сил.