Раздел II Сопротивление материалов

Иметь представление о видах расчетов в сопротивлении материалов, о классификации нагрузок, о внутренних силовых факторах и возникающих деформациях, о механических напряжениях.

Знать основные понятия, гипотезы и допущения в сопротивлении материалов.

«Сопротивление материалов» - это раздел «Технической механики», в котором излагаются теоретико – экспериментальные основы и методы расчета наиболее распространенных элементов конструкций на прочность, жесткость и устойчивость.

Любые создаваемые конструкции должны быть не только прочными и надежными, но не дорогими, простыми в изготовлении и обслуживании, с минимальными расходами материалов, труда и энергии.

Расчеты сопротивления материалов являются базовыми для обеспечения основных требований к деталям и конструкциям.

Тема 4.1 Основные положения. Гипотезы и допущения

Практика показывает, что все части конструкций под действием нагрузок деформируются, т. е. изменяет свою форму и размеры, а в некоторых случаях происходит разрушение конструкции.

Сопротивление материалов есть наука о прочности и дефор­мируемости материалов и элементов машин и сооружений.

Прочностью называется способность материала конст­рукций и их элементов сопротивляться действию внешних сил, не разрушаясь (в дальнейшем понятие прочности будет уточнено).

Выносливость – способность длительное время выдерживать переменные нагрузки.

Устойчивость – способность сохранять первоначальную форму упругого равновесия.

Вязкость – способность воспринимать ударные нагрузки.

В сопротивлении материалов рассматривают методы расчета элементов конструкций на прочность, жесткость и устойчивость.

Расчеты на прочность дают возможность определить размеры и форму деталей, выдерживающих заданную нагрузку, при наименьшей затрате материала.

Под жесткостью понимается способность тела или конструкции сопротивляться образованию деформации.

Расчеты на жесткость гарантируют, что изменения формы и размеров конструкций и их элементов не превзойдут допустимых норм.

Под устойчивостью понимается способность конструк­ции сопротивляться усилиям, стремящимся вывести ее из исходного состояния равновесия.

Расчеты на устойчивость предотвращают возмож­ность внезапной потери устойчивости и искривления длинных или тонких деталей. Примером потери устойчивости может служить внезапное искривление длинного прямолинейного стержня при сжатии вдоль оси.

Расчет на выносливость обеспечивает необходимую долговечность элементов конструкции.

Расчет на устойчивость обеспечивает сохранение необходимой формы равновесия и предотвращает внезапное искривление длинных стержней.

Для обеспечения прочности конструкций, работающих при ударных нагрузок (при ковке, штамповке и подобных случаях), проводиться расчеты на удар.

А практике в большинстве случаев приходится иметь дело с конструкциями сложной формы, но их можно пред­ставить себе состоящими из отдельных простых элементов, например брусьев, пластин, оболочек и массивов.

Основным расчетным элементом в сопротивлении матери­алов является брус, т. е. тело, поперечные размеры которого малы по сравнению с длиной. Брусья бывают прямоли­нейные и криволинейные, постоянного и пере­менного сечения. В зависимости от их назначения в кон­струкции брусья называют колоннами, балками, стер­жнями.

Плоское сечение, перпендикулярное оси бруса, называется поперечным; сечение, параллельное оси бруса (прямолиней­ного),— продольным; остальные плоские сечения — нак­лонными.

Кроме расчета брусьев сопротивление материалов занимает­ся расчетом пластин и оболочек, т. е. тел, имеющих малую толщину по сравнению с другими размерами (например, резервуары, трубы, обшивка кораблей и самолетов). Тела, у которых все три измерения одинакового порядка, называются массивами (например, фундаменты, станины станков). Расче­ты пластин, оболочек и массивов в настоящем учебнике не рассматриваются.

При деформации тела под действием внешних сил внутри него возникают силы упругости, которые препятствуют деформации и стремятся вернуть частицы тела в первоначаль­ное положение. Силы упругости возникают в результате существования в теле внутренних сил молекулярного взаимо­действия.

В сопротивлении материалов изучают деформации тел и возникающие при этих деформациях внутренние силы.

После прекращения действия внешних сил вызванная ими деформация может полностью или частично исчезнуть. Способ­ность материала устранять деформацию после прекращения действия внешних сил называется упругостью. Деформация, исчезающая после прекращения действия внешних сил, называ­ется упругой; деформация, не исчезающая после прекращения действия внешних сил, называется остаточной или пласти­ческой. Способность материала иметь значительные остаточ­ные деформации, не разрушаясь при этом, носит название пластичности, а сами материалы называются 'пластич­ными. К числу таких материалов относятся низкоуглеродистая сталь, алюминий, медь, латунь и др.

Подчеркнем, что возникновение значительных остаточных деформаций в большинстве случаев приводит к нарушению нормальной работы конструкции и поэтому считается наруше­нием прочности (как и разрушение).

Материалы, обладающие весьма малой пластичностью, называются хрупкими. В отличие от пластичных хрупкие материалы разрушаются без заметных остаточных деформаций. К хрупким материалам относят чугун, твердые сплавы, стекло, кирпич и др.

Наука о сопротивлении материалов опирается на законы теоретической механики, в которой тела полагались абсолютно жесткими, т. е. не способными деформироваться. Пользуясь рассмотренным в теоретической механике принципом отверде­вания, в сопротивлении материалов мы будем применять к деформированным телам условия равновесия статики для определения реакций связей и для определения действующих в сечениях деталей внутренних сил.

Однако при расчетах на прочность и жесткость некоторые положения теоретической механики оказываются неприменимы, в частности: 1) действующие на тело внешние силы нельзя заменять их равнодействующей или эквивалентной системой сил; 2) силу нельзя переносить вдоль линии ее действия; 3) пару сил нельзя перемещать в плоскости действия пары.

Эти правила имеют исключение. Так, например, силы, приложенные к небольшой поверхности тела, как и в теорети­ческой механике, мы будем считать сосредоточенными, т. е. приложенными в точке; распределенные реактивные силы, приложенные к защемленному концу балки, мы по-прежнему будем заменять реактивной силой и реактивным моментом. Такие замены не вносят существенных изменений в условия деформации тела. Это положение носит название принципа смягченных граничных условий или принципа Сен-Венана, по имени французского ученого Сен-Венана (1797—1886).

Принцип Сен-Венана можно сформулировать следующим образом: в точках тела, достаточно удаленных от мест приложения внешних сил, модуль внутренних сил весьма мало зависит от конкретного способа приложения сил.

Внешние силы

В сопротивлении материалов под внешними воздейст­виями подразумевается не только силовое взаимодейст­вие, но и тепловое, возникающее из-за неравномерного изменения температурного режима окружающей среды, а также воздействия на элементы сооружений различных осадок опорных связей или перемещения отдельных час­тей сооружения.

Силовые нагрузки делят на объемные и поверхност­ные силы. Объемные или массовые силы — силы, прило­44жение44 ко всем внутренним точкам тела, к ним относятся гравитационные силы тяжести, силы инерции, элект­ромагнитные силы и другие. Поверхностные силы — си­лы, приложенные к поверхности тела. Они делятся на сосредоточенные силы и распределенные нагрузки.

Поверхностная нагрузка, действующая на небольшой площади, условно заменяется сосредоточенной силой, приложенной в центре тяжести этой площади и равной по величине равнодействующей. Например, давление ко­леса локомотива на рельс представляется в виде сосре­доточенной силы, приложенной в центре площади кон­такта колеса с рельсом. Обозначение сосредоточенных сил — Н (ньютон), кН=10³ Н (килоньютон).

Нагрузка, приложенная на значительной площади, называется распределенной. Мерой такой нагрузки слу­жит ее интенсивность, т. е. предел отношения равнодей­ствующей, приходящейся на весьма малую площадку, к величине этой площадки, когда она стремится к нулю. Если интенсивность во всех точках площади нагрузки одинакова, то такая нагрузка носит название равномер­но распределенной. Если же интенсивность разная, то она называется неравномерно распределенной. Обозна­чение распределенных нагрузок — Па = Н/м² (паскаль), Мпа = 10⁶ Па (мегапаскаль). Примером распределен­ных нагрузок является вес снега на кровле здания, соб­ственный вес плит перекрытия и т. п. В тех случаях, когда площадь распределенной нагрузки представляет собой вытянутый прямоугольник, а интенсивность вдоль короткой стороны Ь постоянна и изменяется только по длинной стороне, такую нагрузку условно заменяют по­гонной распределенной нагрузкой интенсивностью q = =pb = Па*м = Н/м.

На сооружения могут действовать моментные нагрузки: в виде распределенных моментов по поверхности (обозначаются Па*м), распределенных погонных момен­тов (обозначаются Па*м/м) или сосредоточенных мо­ментов (обозначаются Н*м).

По характеру действия различают статические и ди­намические нагрузки. Статической нагрузкой называет­ся такая нагрузка, величина которой возрастает пли уменьшается во времени медленно, плавно, т. е. ускоре­ниями точек элемента (силами инерции) можно прене­бречь.

Динамическая нагрузка в отличие от статической из­меняет свою величину во времени с большой скоростью. Действие таких нагрузок сопровождается возникновени­ем колебаний сооружений и дополнительных сил инер­ции, которые необходимо учитывать. Источниками дина­мических нагрузок являются различные машины и меха­низмы с неуравновешенными движущимися частями, а также воздействия от падающих грузов, сейсмические, ветровые и т. п. По продолжительности действия внеш­ние нагрузки делятся на постоянные и временные. По­стоянной называется нагрузка, которая действует непре­рывно в течение всего срока службы сооружения, напри­мер, собственный вес конструкций здания. Временной называется нагрузка, которая действует ограниченное время, после чего исчезает, например, вес снега, давле­ние ветра и т. д.

Внешние нагрузки делятся на неподвижные, не меня­ющие своего местоположения, и перемещающиеся, кото­рые в течение непродолжительного отрезка времени из­меняют свое местоположение на сооружении, сохраняя направление действия, например, давление движущегося локомотива на мост.

Деформации линейные и угловые. Упругость материалов

В отличие от теоретической механики, где изучалось взаимодействие абсолютно жестких (недеформируемых) тел, в сопротивлении материалов исследуется поведение конструкций, материал которых способен деформиро­ваться от внешних воздействий, т. е. изменять взаимное расположение частиц, приводящее к изменению его фор­мы и размеров.

Для случая малых деформаций произвольное измене­ние формы и размеров тела можно разложить на изменение линейных и угловых размеров тела. Изменение линейных размеров называется линейной, а изменение угловых размеров — угловой деформациями. Если на поверхность тела нанести прямоугольную сетку, то пос­ле приложения внешних сил прямоугольники превратят­ся в параллелограммы.

Способность деформироваться от внешних воздейст­вий присуща всем твердым телам из реальных материа­лов. Характер и величина деформаций зависит не толь­ко от внешнего воздействия, но и от физических свойств самого материала. При растяжении равными силами двух стержней одинаковых геометрических размеров из разных материалов, например, из стали и резины, рези­новый стержень удлинится на большую величину, чем стальной.

Важную роль играет процесс поведения деформаций твердого тела при его нагружениb и последующей раз­грузке. Способность тела возвращаться к своей первона­чальной форме и размерам после удаления нагрузки на­зывается упругостью. Если нагруженное тело после сня­тия нагрузки не полностью возвращается к своей перво­начальной форме, то оно называется пластическим. Часть деформации, которая исчезает после снятия на­грузки, является упругой, а та часть, которая остается, называется остаточной или пластической деформацией. Упругостью и пластичностью обладают все реальные ма­териалы. При небольших нагрузках влияние пластичес­ких свойств материала обычно незначительно и им пре­небрегают, считая, что тело полностью восстанавливает свою первоначальную форму и размеры после снятия нагрузки.

Расчетная схема сооружений. Опорные связи

Для создания общего подхода по изучению поведения конструктивных элементов все разнообразие реальных сооружений можно разбить на несколько групп: массив­ные тела, имеющие все три размера одного порядка (гидротехнические плотины, грунтовые основания), двух­мерные, имеющие два размера одного порядка (пластин­ки, оболочки) и третий, значительно меньший, чем пер­вые два; и одномерного элемента, имеющего два размера ничтожно малой величины по сравнению с третьим размером — длиной (брус).

В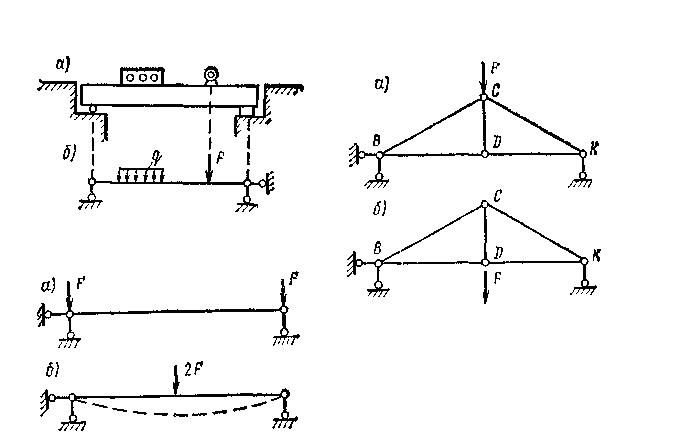 сопротивлении материалов объектом изучения слу­жит в основном элемент третьей группы — одномерный элемент, брус. Брус представляет собой тело, образован­ное движением плоской фигуры по некоторой кривой (или прямой), совпадающей с центром тяжести этой фи­гуры. Для такого элемента кривая, по которой двигалась плоская фигура, является осью бруса, а сама плоская фигура — его поперечным сечением. На практике по­перечное сечение принимается в виде простых фигур: квадрата, прямоугольника, круга, или в виде сложных: двутавра и т. д. По длине брус может иметь постоянное, переменное или ступенчатое поперечное сечение. Расчет­ная схема бруса изображается в виде его осевой линии, проходящей через центры тяжести поперечных сечений. Брус соединяется с другими элементами и основанием условными опорными связями. Непосредственно к осевой линии прикладываются внешние нагрузки и опорные ре­акции.

В качестве опорных связей используются следующие виды: шарнирно-подвижная, шарнирно-неподвижная и жесткая опора (заделка).

В дальнейшем изложении будут употребляться термины балка, стержень, которые являются тем же бру­сом, но отличаются

рис.4.1 рис.4.2 специфическими условиями дефор­мирования. Балка работает на изгиб, а стержень — на растяжение-сжатие.

Таким образом, в сопротивлении материалов, а также и в строительной механике исследуются не действитель­ные сооружения, а их расчетные схемы. Замена реаль­ного сооружения его расчетной схемой является ответст­венной и сложной проблемой, от правильного решения которой зависит достоверность результатов последующих расчетов. На примере покажем, как реальная балка, изо­браженная (на рис. 4.1 а – верхний рис.) заменяется ее расчетной схе­мой (рис. 4.1, б- верхний рис.).

Следует обратить внимание на ограничение примене­ния правил теоретической механики. В сопротивлении материалов нельзя переносить момент пары сил в дру­гую точку или точку приложения сосредоточенной силы по линии ее действия, так как перенос нагрузки в новое положение вызывает изменение в распределении вну­тренних сил в конструкции. Например, при загружении фермы силой F в верхнем узле С (рис. 4.2, а) в стерж­не CD не возникает никаких сил. Если же силу F перене­сти по линии ее действия и приложить к нижнему узлу D (рис. 4.2,6), то в стержне CD появится растягиваю­щая сила, равная F.

Также нельзя систему сил заменять ее равнодейству­ющей при определении перемещений конструкции. На­пример, в балке, нагруженной двумя силами F в опорных сечениях В и С, не возникает никаких перемещений ее оси (рис. 4.1, а- нижний рис.). Если же эти две силы заменить равно­действующей 2 F, приложенной посередине пролета бал­ки (рис. 4.1,6- нижний рис.), то балка изогнется. Правила теоретиче­ской механики всегда остаются справедливыми при со­ставлении условий равновесия.

Допущения и ограничения, принятые в сопротивлении материалов

Реальные строительные материалы, из которых воз­водятся различные здания и сооружения, представляют собой довольно сложные и неоднородные твердые тела, обладающие различными свойствами. Учесть это разно­образие свойств трудно, поэтому в сопротивлении мате­риалов используются не все характеристики твердых тел, а, только общие признаки, присущие всем телам с уста­новившимися внутренними связями между ними. Иными словами, в сопротивлении материалов изучается поведе­ние конструкции из идеализированного материала, с со­хранением главных физико-механических характеристик.

1.1 Допущение о непрерывном (сплошном) строении материала. По этому допущению принимается, что весь объем любого элемента конструкции заполнен вещест­вом без каких-либо пустот, т. е. не учитывается действи­тельная дискретная атомистическая структура материа­лов. Это допущение позволяет выделять из любой части сооружения бесконечно малый элемент и, приписывая ему свойства материала всего сооружения, пользоваться при исследовании напряженно-деформированного состояния математическими методами анализа бесконечно малых величин.

2. Допущение о ненапряженном состоянии тела. Со­гласно этому допущению, в материале элемента до его нагружения нет никаких напряжений, т. е. действитель­ные (начальные) напряжения, характер и величина ко­торых зависят от причин возникновения, принимаются равными нулю. Иными словами, возникающие напряже­ния в результате нагружения тела внешними силами принимаются за фактические напряжения в то время как они в действительности составляют лишь прирост напря­46жение, вызванных этими силами.

3. Допущение об однородности материала. Согласно этому допущению принимается, что материал во всех точках любого объема имеет одинаковые физико-механи­ческие характеристики.

4. Допущение об изотропности материала. Согласно этому допущению, материал в любой точке и по всем на­правлениям, проведенным через эту точку, имеет одина­ковые физико-механические характеристики. Реальные материалы не являются абсолютно изотропными. Напри­мер, у технических сплавов стали физико-механические характеристики не одинаковы по разным направлениям, что обусловлено ее структурой и условиями обработки, но этими различиями обычно пренебрегают и считают сплавы стали изотропными. Если различия характерис­тик материала в разных направлениях будут значитель­ными, то такие конструкции следует рассчитывать по теории анизотропных тел. В данном случае материал наделяется свойствами абсолютной изотропии.

5. Допущение об идеальной упругости материала. Со­гласно этому допущению предполагается, что материал обладает способностью полностью восстанавливать свою первоначальную форму и размеры тела после устранения причин, вызвавших его деформацию. Деформация иде­ально упругого тела зависит лишь от тех нагрузок, ко­торые в данный момент действуют на тело и не зависят от того, каковы были нагрузки в предшествовавшие мо­менты времени. Данная гипотеза применима только при напряжениях, не превышающих предела упругости мате­риала.

6. Допущение о линейной зависимости между напря­47жение4747 и деформациями. Согласно этому допущению, упругое тело наделяется наиболее простой, а именно ли­нейной зависимостью между напряжениями и деформа­циями в данной точке, которая носит название закона Гука. Для такого материала диаграмма растяжения-сжатия, построенная в координатах «напряжение-де­формация», имеет вид наклонной прямой линии, прохо­дящей через начало координат. Для реальных материа­лов диаграмма имеет нелинейный характер, но на начальном этапе нагружения при сравнительно неболь­ших напряжениях, соответствующих действительной работе материала в конструкции, диаграмму с неболь­шой кривизной заменяют прямолинейной зависимостью Таким образом, в сопротивлении материалов закон Гука применим при напряжениях, не превосходящих некото­рого предела, называемого пределом пропорционально­сти. Если же исследуется поведение конструкции за пре­делом пропорциональности или же криволинейность диаграммы значительна, то расчеты проводят по физи­чески нелинейной теории.

7. Допущение о малости перемещений по сравнению с геометрическими размерами элементов сооружений. Со­гласно этому допущению, не учитываются изменения геометрических размеров элементов и местоположения нагрузок из-за искривления, растяжения, сжатия и сдви­га после приложения к ним внешних сил. Поскольку в со­противлении материалов исследуются элементы в виде бруса, то сравнение перемещений производится с его длиной. Таким образом, реакции и внутренние силовые факторы определяются по заданной, начальной геомет­рии, что значительно упрощает расчет, так как все урав­нения приобретают линейный вид. В тех же случаях, когда перемещения сравнимы с длинами элементов, рас­чет следует производить по деформированной схеме, пользуясь геометрически нелинейной теорией.

8. Следствием трех последних допущений об идеаль­ной упругости материала, линейной зависимости между напряжениями и деформациями и малости перемещений является принцип независимости действия сил или прин­цип суперпозиции.

Согласно этому принципу, эффект от действия суммы сил равен сумме эффектов действия каждой силы от­дельно. Иными словами, в сопротивлении материалов можно вычислять реакции, внутренние силовые факто­ры, напряжения и перемещения как алгебраическую сум­му этих факторов от раздельного действия внешних сил независимо от порядка их приложения к 47жен­жению.

9. Гипотеза плоских сечений (гипотеза Бернулли). Со­гласно этой гипотезе, поперечное сечение элемента (бал­ки, стержня), плоское и перпендикулярное к его оси до приложения к элементу внешних сил, остается плоским и перпендикулярным к оси и после приложения к эле­менту нагрузок.

10. Гипотеза Сен-Венана. Согласно этой гипотезе, в достаточно удаленных точках элемента от места приложения нагрузки внутренние силовые факторы весьма мало зависят от способа приложения этой нагрузки.

Виды нагрузок и основных деформаций

В процессе работы машин и сооружений их узлы и детали воспринимают и передают друг другу различные нагрузки, т. е. силовые воздействия, вызывающие изменение внутренних сил и деформации узлов и деталей.

Силы, воспринимаемые элементами конструкций, являются либо массовыми, или объемными (силы тяжести, силы инерции), либо поверхностными силами контактного взаимо­действия рассматриваемого элемента с соседними элементами или прилегающей к нему средой (например, пар, воздух, жидкость).

В теоретической механике мы установили, что поверхност­ные нагрузки бывают сосредоточенными или распреде­ленными.

В зависимости от характера действия нагрузки подразде­ляют на статические и динамические.

Статическими (рис.4.3,а) называются нагрузки, числовое значение, направление и место приложения которых остаются постоянны­ми или меняются медленно и незначительно. Таким образом, можно полагать, что при передаче статических нагрузок все части конструкции находятся в равновесии.

Пример статической нагрузки — сила тяжести сооружений.

Динамическими (рис.4.3,в) называются нагрузки, характеризую­щиеся быстрым изменением во времени их значения, направле­ния или места приложения.

К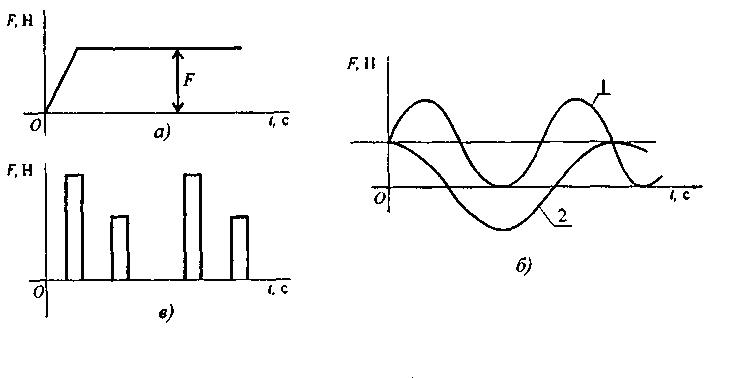 динамическим относятся ударные, внезапно прило­48жение48 и повторно-переменные нагрузки. Ударные нагрузки возникают, например, при ковке металла или забивке свай; примером внезапно прилагаемой нагрузки является давление колеса, катящегося по рельсу; повторно-переменные нагрузки испытывают, например, детали кривошипно-ползунного механизма паровой машины. К динамическим относятся также инерционные нагрузки, например силы инерции в ободе вращающегося

рис.4.3 маховика.

1. Повторно – переменные нагрузки (рис.4.3, б) многократно меняют значение или значение и знак. Действие таких нагрузок вызывают усталость металла.

Следует помнить, что в число внешних сил, принимаемых во вниманию при расчете конструкций, входят не только активные силы, но также реакции связей и силы инерции (при движении с достаточно большим ускорением).

Далее перейдем к рассмотрению основных деформаций. Из практики известно, что в процессе эксплуатации элементы конструкций испытывают следующие основные деформации:

1) растяжение; эту деформацию испытывают, например, канаты, тросы, цепи, шток протяжного станка;

2) сжатие; на сжатие работают, например, колонны, кирпичная кладка, пуансоны штампов;

3) сдвиг; деформацию сдвига испытывают заклепки, болты, шпонки, швы сварных соединений. Деформацию сдвига, доведенную до разрушения материала, называют срезом. Срез возникает, например, при резке ножницами или штамповке деталей из листового материала;

4) кручение; на кручение работают валы, передающие мощность при вращательном движении. Обычно деформация кручения сопровождается другими деформациями, например изгибом;

5) изгиб; на изгиб работают балки, оси, зубья зубчатых колес и другие элементы конструкций.

Формы элементов конструкции

Все многообразие форм сводится к трем видам по одному при­знаку.

1. Брус — любое тело, у которого длина значительно больше других размеров.

В зависимости от форм продольной оси и поперечных сечений различают несколько видов брусьев:

— прямой брус постоянного поперечного сечения (рис. 4.4, а);

— прямой ступенчатый брус (рис. 4.4, 6);

— криволинейный брус (рис. 4.4, в).

2. Пластина — любое тело, у которого толщина значительно меньше других размеров (рис.4.5).

3. Массив — тело, у которого три размера одного порядка.

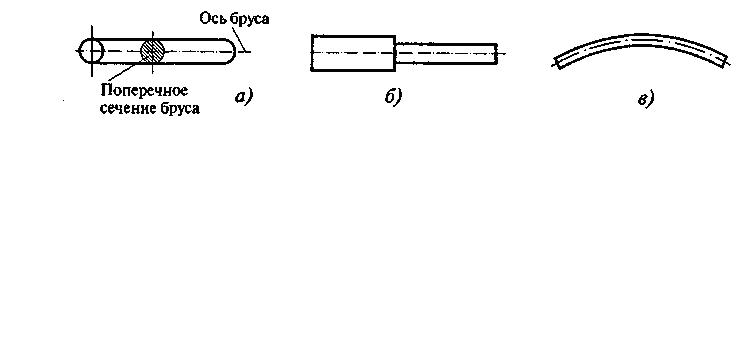
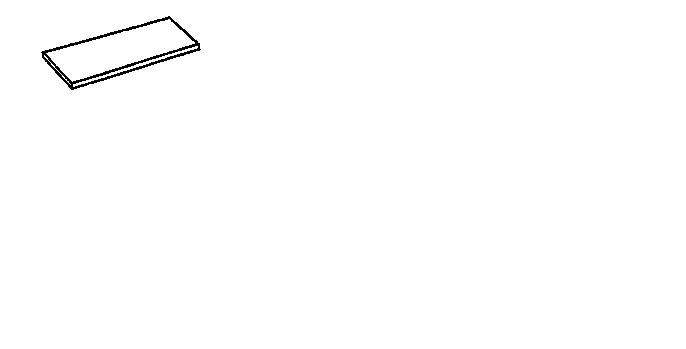
Рис.4.4 рис.4.5