Тема 2.2 Простейшие движения твердого тела

Иметь представление о поступательном движении, его особенности и параметрах, о вращательном движении тела и его параметрах.

Знать формулы для определения параметров поступательного и вращательного движений тела.

Уметь определять кинематические параметры тела при поступательном и вращательном движениях, определять параметры любой точки тела.

Поступательным называют такое движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему начальному положению.

При поступательном движении все точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы.

При поступательном движении тела прямая, соединя­ющая две произвольные точки тела, будет перемещаться параллельно самой себе. Примерами поступательного движения могут служить движение кузова автомобиля, который едет прямолинейно, движение кабины лифта, движение поршня в цилиндре двигателя и т. д. Докажем, что при поступательном движении все точки тела двига­ются по одинаковым траекториям и имеют в любой мо­мент времени одинаковые векторы скорости и ускорения. В теле, которое движется поступательно, возьмем две любые точки А и В (рис. 2.12). Соединим эти точки от­резком прямой линии. При перемещении тела длина это­го отрезка остается постоянной, так как в кинематике рассматриваются абсолютно твердые тела. Через неко­торый промежуток времени тело займет новое положе­ние, а вместе с ним займет новое положение A₁ В₁ отре­зок прямой линии АВ. Совершим теперь параллельный перенос всех точек траектории ВВ₁ чтобы точка В заняла положение А. Так как отрезки прямых АВ и A₁ В₁ параллельны и равны друг другу, то очевидно, что при параллельном переносе точка В₁ перейдет в точку A₁. Такое рассуждение можно провести для любого по­ложения В₁ а значит при параллельном переносе траек­тория точки В полностью совпадает с траекторией точки А, т. е. они тождественны. Естественно, раз мы брали любые точки А и В, это справедливо для всех точек те­ла. Кроме этого, совпадает и положение точек А и В на этой траектории в любой момент времени (В₁ тождест­венно A₁). Если считать, что в начальный момент време­ни все точки тела находятся в начале отсчета своих траекторий, то законы движения точек А и В будут оди­наковыми: s_A =s_B.

Продифференцируем это равенство по времени: , или . Следовательно, так как положение точек А и В про­извольно, то векторы скоростей всех точек в данный мо­мент времени равны друг другу. Вектор v называется вектором скорости поступательного движения тела.

Если продифференцировать равенство (2.12) по вре­мени, то получим

, или .

т. е. векторы ускорений всех точек тела в данный момент времени равны друг другу. Вектор а называется векто­ром ускорения поступательного движения тела. Из выше доказанного следует, что поступательное движение твер­дого тела определяется движением одной его точки. Обычно за такую точку принимают центр тяжести тела. рис.2.12

Вращательное движение

Движение, при котором по крайнем мере точки твердого тела или неизменяемой системы остаются неподвижными, называемыми вращательным; прямая линия, соединяющая эти две точки, называется осью вращения.

Вращательное движение в технике встречается весьма часто. В подавляющем большинстве механизмов и машин имеются звенья, которые совершают вращательное движение, например, валы, зубчатые колеса, кривошипы и т.д. Заметим, что понятие вращательного движения может относиться только к телу, но не к точке; так, например, движение точки по окружности есть не вращательное движение, а криволинейное.

Если через ось вращения провести плоскость Р, жест­ко связанную с телом, то при вращении тела эта плос­кость будет занимать новые положения (рис. 2.13). Угол между первоначальным положением плоскости Р и ее новым положением Р₁ в текущий момент времени назы­вается углом поворота тела и обозначается ср. Измеряет­ся этот угол в радианах и считается положительным, если плоскость Р поворачивается против часовой стрел­ки (при этом надо смотреть с положительного конца оси z, направленной вдоль оси вращения тела). Кроме оси вращения для полного определения движения тела надо еще знать угол поворота φ как функцию времени t:φ=f(t) – закон вращательного движения тела. рис.2.13

Итак, при вращательном движении твердого тела точки его, находящиеся на различном расстоянии от оси вращения, имеют неодинако­вые траектории, скорости и ускорения.

Отсюда следует, что линейное перемещение (путь), линей­ные скорость и ускорение точек не могут характеризовать враща­тельное движение тела в целом. Вращательное движение можно характеризовать углом φ, на который повернулось тело за дан­ный промежуток времени. Этот угол называется угловым пере­мещением тела. Угловое перемещение выражается в радианах (рад) или оборотах (об); в последнем случае угловое перемеще­ние обозначают N. Они связаны соотношением: φ =2πN (рад), N – число оборотов тела.

Путь любой точки вращающегося тела: s=rφ

Угловая скорость есть кинематическая мера движения вращаю­щегося тела, характеризующая быстроту его углового перемеще­ния: ( рад/с)

Линейная скорость любой точки вращающего тела опреде­ляется формулой: υ=ωr, т. е. скорость точки прямо пропорциональна ее расстоянию от оси вращения.

В технике скорость вращения часто вращения оборотах в минуту, обозначают буквой п и называют частотой вращения. Угловая скорость и частота вращения, выраженные соответ­ственно в рад/с и мин^-1, связаны соотношением:

ω=πn/30 (рад/с)

Изменение угловой скорости во времени определяется уголковым ускорением ε = рад /с²:

Вектор углового ускорения направлен вдоль оси вращения, при вращения тела модуль угловой скорости может уменьшаться или увеличиваться. В первом случае вращения будет замедленным, а втором – ускоренным. При ускоренном движении направление вектора ускорения совпадает с направлением вектора скорости, а при замедленном – векторы скорости и ускорения будут направлены в разные стороны.

Равномерным вращением тела называется такое дви­жение, при котором угловая скорость вращения тела остается постоянной. Если угловое ускорение тела посто­янно, то такое вращение называется равнопеременным. Законы для равномерного и равнопеременного вращений получаются так же, как и аналогичные законы движения точки, поэтому при равномерном движении имеем: , где - начальный угол поворота; - постоянная уголовая скорость тела.

Заменяя в на , получим закон равнопеременного движения: .

Здесь — начальная угловая скорость. В любой мо­мент времени угловая скорость будет определяться по формуле:

Если при равнопеременном вращении скорость и ус­корение направлены в одну сторону, то вращение назы­вается равноускоренным и соответственно если направ­ления скорости и ускорения не совпадают, то равнозамедленным.

Частные случаи вращательного движения

Равномерное вращение (угловая скорость постоянна):

ω = const.

Уравнение (закон) равномерного вращения в данном случае име­ет вид:

φ = φ₀ + φt,

где φ₀ — угол поворота до начала отсчета.

Кинематические графики для этого вида движения изображены на рис. 2.14.

рис.2.14

Равнопеременное вращение (угловое ускорение постоянно):

ε = const.

Уравнение (закон) равнопеременного вращения

,

где ω₀ — начальная угловая скорость.

Угловое ускорение при ускоренном движении — величина поло­жительная; угловая скорость

будет все время возрастать.

Угловое ускорение при замедленном движении — величина от­рицательная; угловая скорость убывает.

Для данного движения кинематические графики представлены на рис. 2.1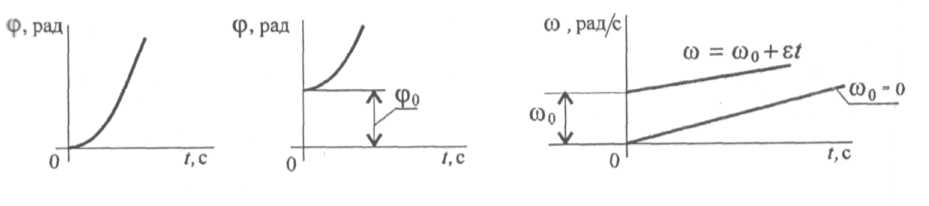5. рис. 2.15

Скорости и ускорения точек вращающегося тела

Тело вращается вокруг точки О. Определим параметры дви­жения точки Л, расположенной на

расстоянии г а от оси вращения (рис. 11.6, 11.7).

Рис.2.16

Путь точки А: S_A = φr_A.

Линейная скорость точки А: v_A = ωr_A.

Ускорение точки А: a_tA = εr_A – касательное; : a_tA = εr_A

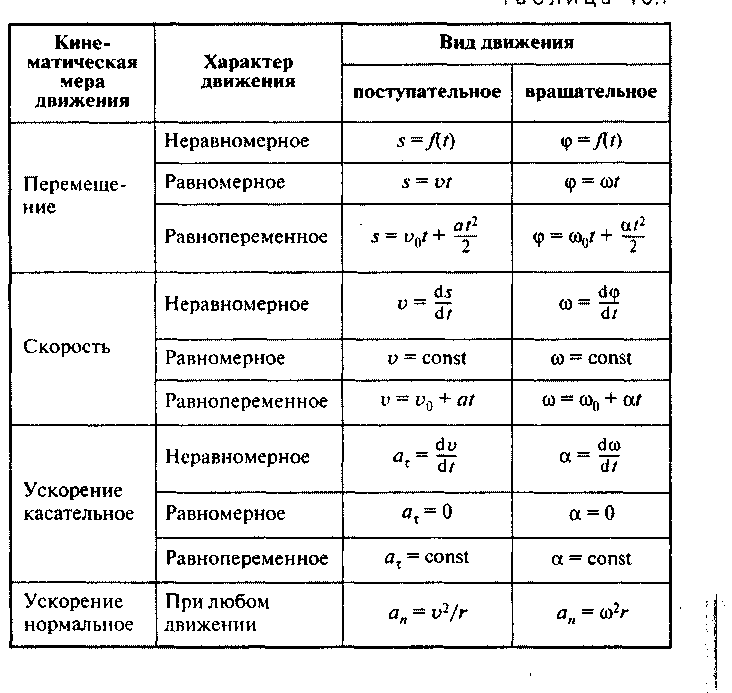
Сравнение формул кинематики для поступательного и вращательного движений

Преобразование вращательного движения

Преобразование вращательного движения осуществля­ется разнообразными механизмами, которые называются пере­дачами. Наиболее распространенными являются зубчатые и фрикционные передачи, а также передачи гибкой связью (на­пример, ременные, канатные, ленточные и цепные). С помощью этих механизмов осуществляется передача вращательного движения от источника движения (ведущего вала) к приемнику дви­жения (ведомому валу).

Передачи характеризуются передаточным отношением или передаточным числом.

Передаточным отношеньем i называется отношение уг­ловой скорости ведущего звена к угловой скорости ведомого зве­на. Передаточное отношение может быть больше, меньше или равно единице.

Передаточным числом и двух сопряженных звеньев назы­вается отношение большей углевой скорости к меньшей. Пере­даточное число передачи всегда больше или равно единице.

В целях унификации обозначений передаточные отношения и передаточные числа всех передач мы будем обозначать буквой «и», в некоторых случаях с двойным индексом, соответствую­щим индексам звеньев передачи: .

Заметим, что индекс 1 приписывают параметрам ведущего звена передачи, а индекс 2 — ведомого.

Передача, у которой угловая скорость ведомого звена меньше угловой скорости ведущего, называется понижающей в противном случае передача называется повышающей.

В технике наибольшее распространение получили: 1) зубча­тые, 2) ременные и 3) цепные передачи.

1. Общие сведения о простейших зубчатых передачах их основных видах, а также конструктивных элементах зубчатых ко­лес, реек и червяков известны из курса черчения. Рассмотрим зубчатую передачу, схематически изображенную на рис. 2.17.

В месте соприкосновения зубчатых колес I и II скорости то­чек первого и второго колеса одинаковы. Обозначив модуль этой скорости v, получим . Следовательно, можно записать так: .

Из курса черчения известно, что диаметр делительной окружности зубчатого колеса равен произведению его модуля на число зубьев: d = mz. Тогда для пары зубчатых колес:

Рис.2.17

2. Рассмотрим ременную пе­редачу, схематически изображен­ную на рис. 10.6. При отсутствии

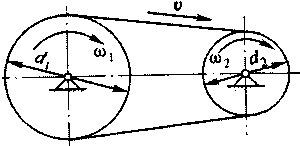
рис.2.18

проскальзывания ремня по шки­вам ,следовательно, для ременной пе­редачи .

3. Для цепных передач , где число зубьев ведущей передачи и ведомой звездочек передачи.