3.2. Збір та логіко-графічний аналіз вхідних даних

Державна соціальна допомога малозабезпеченим сім`ям у 2010-2011 становила відповідно 7611,769 та 8221,740 тис.грн. Тобто у 2011 році виплати збільшились на 609,971 тис.грн. Як бачимо, є досить стабільна тенденція зростання виплати цієї допомоги, що пов’язано з часом виплати, а також з підвищенням соціальних гарантій населенню (рис.3.1). Це дає можливість на майбутнє припускати подальший ріст виплати соціальної допомоги.

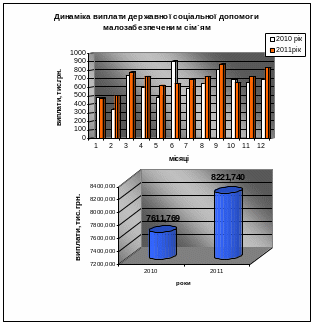
Рис. 3.1. Динаміка виплати державної соціальної допомоги малозабезпеченим сім`ям

Протягом 2009-2011 рр. державна допомога по догляду за дитиною до досягнення нею 3-річного віку зростала, зокрема у 2010 виплата складала 17801,747 тис.грн., що на 8479,884 тис.грн. більше, ніж у 2009 році. У 2011році виплата дорівнювала 21023,765 тис.грн., тобто вона на 7222,018 ти.грн. перевищила виплату у 2010 році.

Як бачимо з рисунка 3.2, є досить стабільна тенденція зростання обсягів виплати допомоги, що пов’язано із підвищенням соціальних гарантій населенню, так і із зростанням кількості виплат.

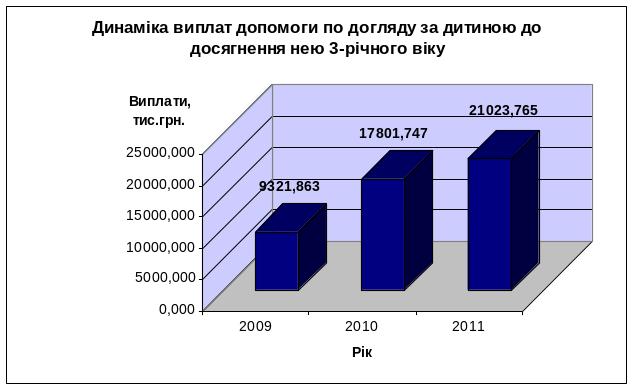
Рис.3.2. Динаміка виплат допомоги по догляду за дитиною до досягнення нею 3-річного віку

Тому, у своїй моделі я вирішила дослідити вплив часу (х) на виплату державної соціальної допомоги малозабезпеченим (у), а також кількості виплат (x) на виплату допомоги по догляду за дитиною до досягнення нею 3-річного віку (y).

3.3.Аналіз результатів дослідження та формування пропозицій щодо впливу факторних показників (х) на результуючий показник (у)

Для побудови економіко-математичної моделі обираємо динаміку виплат державної соціальної допомоги малозабезпеченим сім`ям (У) і періоду виплат (Х), що її виплачували протягом 12 місяців 2011 року (таблиця 3.1).

Таблиця 3.1.

Статистичні дані для дослідження економіко-математичної моделі

Місяць		Сума виплат
Січень	1	470,837
Лютий	2	499,563
Березень	3	778,643
Квітень	4	724,745
Травень	5	618,905
Червень	6	643,858
Липень	7	696,177
Серпень	8	720,099
Вересень	9	871,388
Жовтень	10	651,105
Листопад	11	718,599
Грудень	12	827,821
Всього		8221,74

З графіку (рис. 3.3), побудованому на основі даних таблиці видно, що сума виплат допомоги змінюються в залежності від періоду виплат.

Рис. 3.3. Динаміка виплати державної соціальної допомоги залежно від періоду

Зібравши та провівши логіко-графічний аналіз статистичних даних по виплатах державної соціальної допомоги, за 12 місяців 2011 року (з січня по грудень), було помічено існування залежності між пока­зниками величин виплати і періодом виплат. Тому, будемо досліджувати вплив періоду виплат (х) на величину виплат (у).

Оскільки, показники, потрібні для побудови економіко-математичної моделі, були визначені, то проводимо комп'ютерні розрахунки параметрів регресійної залежності між обраними показниками. (додаток…) Економетричний аналіз набору статичних даних, які використовувались для дослідження дина­міки залежності обсягів мобілізації податку з суб’єктів малого підприємництва від кількості перевірок дав наступні результати (таблиця 3.2).

Таблиця 3.2

Економетричний аналіз набору статичних даних

Коефіцієнт кореляції (Rxy)	0,97
Коефіцієнт детермінації (R^2)	0,94
Статист.значущість, F-критерій	151,37
Табличне значення Fтаб=F(1;12-2;5%)	4,96
Квадрат дисперсії залишків	14130,48
Залишкова дисперсія	8289,698
Рівень значущості, F-критерій	0,704583

Кореляційний аналіз дає змогу кількісно оцінити тіс­ноту зв'язку між показником і фактором. Обчислений коефіцієнт кореляції, R_ху=0,97, має додатне значення, а це свідчить про те, що існує прямий зв'язок між даними, тобто при збільшенні кількості виплат, величина виплат зростатиме прямопропорційно. Оскільки коефіцієнт кореляції наближається до одиниці, то має місце тісна (си­льна) лінійна функціональна залежність між х та y. Далі за допомогою функції ЛИНЕЙН знаходимо показники а₀, а₁ та а₂ і будуємо лінійне рівняння регресії у = а₀+а₁t+a₂t², де t - порядковий номер місяця

Коефіцієнти рівняння регресії дорівнюють: а₀=474,235, а₁=52,34, а₂=-2,387.

Рівняння регресії: y=474,235+52,34t-2,387t².

Значення коефіцієнта детермінації (R²=0,94) показує неликий вклад помилок (6%) у побудові економетричної моделі. Статистичну значущість коефіцієнта детермінації перевіряємо за допомогою F-критерію ( =151,37 при n=12, m=1), що поряд з табличним значенням критерію Фішера F()=F(0,05;1;12-1-1)=4,96 є значно більшим. Тобто такий фактор як період виплат достатньо повно пояснює стохастичну залежність. Отже, коефіцієнт детермінації статистично значимий і включені в регресію фактори доста­тньо повно пояснюють стохастичну залежність змінних, а це визначає дану мо­дель як адекватну.

Для побудови наступної економіко-математичної моделі обираємо динаміку виплат допомоги по догляду за дитиною до досягнення нею 3-річного віку (У) і кількістю одержувачів (Х), що її виплачували протягом 2011 року (таблиця 3.3).

Таблиця 3.3

Статистичні дані для дослідження економіко-математичної моделі

Місяць		К-сть одержувачів	Сума виплат
Січень	1	3198	1529,956
Лютий	2	3156	1439,526
Березень	3	4052	2028,582
Квітень	4	3614	1903,398
Травень	5	3395	1720,957
Червень	6	3470	1705,573
Липень	7	3299	1813,726
Серпень	8	3216	1622,821
Вересень	9	3508	1858,907
Жовтень	10	3736	1731,164
Листопад	11	3769	1768,616
Грудень	12	3852	1900,539
Всього		42265	21023,765

З графіку (рис. 3.4), побудованому на основі даних таблиці видно, що сума виплат допомоги змінюються в залежності від кількості одержувачів.

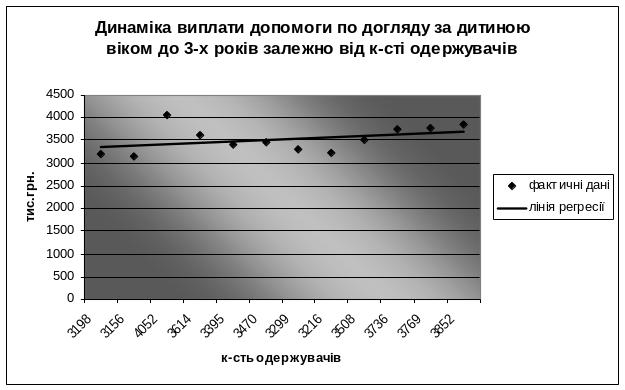
Рис.3.4. Динаміка виплат допомоги по догляду за дитиною до досягнення нею 3-річного віку залежно від к-ті одержувачів

Зібравши та провівши логіко-графічний аналіз статистичних даних по виплатах допомоги по догляду за дитиною до досягнення нею 3-річного віку, за період з січня по грудень 2011 року, було помічено існування залежності між пока­зниками величин надходжень виплати і кількістю одержувачів. Тому, будемо досліджувати вплив кількості одержувачів (х) на величину виплат (у).

Оскільки, показники, потрібні для побудови економіко-математичної моделі, були визначені, то проводимо комп'ютерні розрахунки параметрів регресійної залежності між обраними показниками (додаток…).

Економетричний аналіз набору статичних даних, які використовувались для дослідження дина­міки залежності обсягів мобілізації податку з суб’єктів малого підприємництва від кількості перевірок дав наступні результати (таблиця 3.4). Кореляційний аналіз дає змогу кількісно оцінити тіс­ноту зв'язку між показником і фактором. Обчислений коефіцієнт кореляції, R_ху=0,81, має додатне значення, а це свідчить про те, що існує прямий зв'язок між даними, тобто при збільшенні кількості одержувачів, величина виплат зростатиме прямопропорційно. Оскільки коефіцієнт кореляції наближається до одиниці, то має місце тісна (си­льна) лінійна функціональна залежність між х та y. Отже, далі знаходимо невідомі параметри а і b рівняння регресії за допомогою методу найменших квадратів і будуємо лінійне рівняння регресії у = а + bх. Коефіцієнти рівняння регресії дорівнюють: а=96,19; b=0,47.

Таблиця 3.4

Економетричний аналіз набору статичних даних

Коефіцієнт кореляції (Rxy)	0,81
Коефіцієнт детермінації (R^2)	0,66
Статист.значущість, F-критерій	19,29
Табличне значення Fтаб=F(1;24-2;5%)	4,96
Квадрат дисперсії залишків	27652,9191
Залишкова дисперсія	10385,9646
Рівень значущості, F-критерій	1,66252777

Як бачимо з графіку знайдені розрахункові дані дещо відрізняються від фактичних даних, але все ж дозволяють достатньо дослідити залежність між вибраними показниками.

Значення коефіцієнта детермінації (R²=0,66) показує досить великий вклад помилок (33%) у побудові економетричної моделі. Статистичну значущість коефіцієнта детермінації перевіряємо за допомогою F-критерію ( =19,29 при n=12, m=1), що поряд з табличним значенням критерію Фішера F()=F(0,05;1;12-1-1)=4,96 є значно більшим. Тобто такий фактор як кіль­кість одержувачів достатньо повно пояснює стохастичну залежність. Отже, коефіцієнт детермінації статистично значимий і включені в регресію фактори доста­тньо повно пояснюють стохастичну залежність змінних, а це визначає дану мо­дель як адекватну.