
- •Кафедра «Высшая математика»
- •Содержание
- •§1. Предмет математической статистики
- •§2. Выборочная совокупность и ее характеристики
- •§3. Законы распределения выборочных характеристик
- •§4. Статистическое оценивание числовых характеристик случайной величины и закона распределения
- •§5. Статистические гипотезы
- •§6. Методы регрессионного и корреляционного анализа
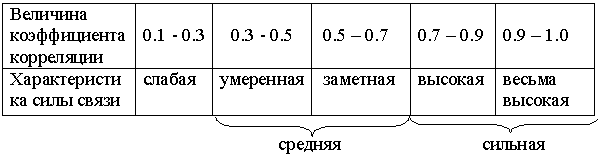
- •Количественные критерии оценки тесноты связи (шкала Чеддока)
- •Контрольные задания Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Указание. Для упрощения вычислений перейти к условным вариантам
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Рекомендуемая литература
- •Критические точки распределения 2
- •Критические точки распределения Стьюдента
- •Критические точки распределения Фишера-Снедекора
- •Элементы математической статистики
- •192171, Г. Санкт-Петербург, ул. Седова, 55/1
Количественные критерии оценки тесноты связи (шкала Чеддока)
Для оценки значимости r применяется t-критерий Стьюдента. При этом определяется фактическое значение критерия tr:
![]() .
.
Исчисленное tr сравнивается с критерием tк, которое берется из таблицы значений t-Стьюдента с учетом заданного уровня значения и числа степеней свободы k (см. прил. 5). Если tr>tк, то величина коэффициента корреляции признается существенной.
К уравнениям регрессионного анализа относятся прямая, гипербола, парабола, экспонента, логарифмическая функция и др.
Применение
метода наименьших квадратов позволяет
получить достаточно точные теоретические
значения линии однофакторной регрессии
и, соответственно, ее графическое
изображение. Подобранной считается та
модель расчетов теоретической линии,
для которой квадрат отклонений
эмпирических данных у от теоретической
линии регрессии
![]() минимальный, т.е.
минимальный, т.е.
![]() .
Для определения параметров уравнения
на основе требований метода наименьших
квадратов составляется система нормальных
уравнений:
.
Для определения параметров уравнения
на основе требований метода наименьших
квадратов составляется система нормальных
уравнений:
 .
.
Решая систему линейных уравнений получим:
![]() ,
,
![]() .
.
Множественные уравнения регрессии позволяют вычислить теоретические значения результативного признака в зависимости от всех включенных в множественное уравнение факторов (без графического его изображения одной теоретической линией).
Различный
подход к истолкованию результатов
регрессионного анализа исходит из
разного понимания смысла параметров
уравнений регрессии, полученных методом
наименьших квадратов. Например считается,
что в уравнении однофакторной линейной
регрессии
![]() ,
параметр b
означает среднее изменение величины
результативного признака у,
в зависимости от изменения значений
факторного признака х,
если все остальные факторы, влияющие
на результативный признак у
и не связанные с факторным, рассматриваются
как неизменные (т.е. этот
параметр показывает, насколько в среднем
величина одного признака (Y)
изменяется при изменении на единицу
меры другого корреляционно связанного
с Y
признака X).
При исследованиях это требование трудно
учесть. Параметр а
(свободный член) отражает усредненное
влияние всех неучтенных факторов. Если
первое требование трудно учесть, то
второе - истолковать, особенно в тех
случаях, когда он имеет отрицательное
значение.
,
параметр b
означает среднее изменение величины
результативного признака у,
в зависимости от изменения значений
факторного признака х,
если все остальные факторы, влияющие
на результативный признак у
и не связанные с факторным, рассматриваются
как неизменные (т.е. этот
параметр показывает, насколько в среднем
величина одного признака (Y)
изменяется при изменении на единицу
меры другого корреляционно связанного
с Y
признака X).
При исследованиях это требование трудно
учесть. Параметр а
(свободный член) отражает усредненное
влияние всех неучтенных факторов. Если
первое требование трудно учесть, то
второе - истолковать, особенно в тех
случаях, когда он имеет отрицательное
значение.
Критерием правильного применения регрессионного и корреляционного анализа при изучении взаимосвязей между наблюдениями является наличие нормального распределения совокупности, которое наблюдается только в том случае, если на эту взаимосвязь действует множество случайных, независимых или же слабо зависимых факторов и отсутствуют факторы, играющие в общем итоге преобладающую роль.
При исследовании корреляции между количественными признаками, значения которых можно точно измерить в единицах метрических шкал (рубли, секунды, килограммы и т.д.) очень часто принимается модель двумерной нормально распределенной генеральной совокупности. Такая модель графически отображает зависимость между переменными величинами xi и yi в системе прямоугольных координат. Эту графическую зависимость называют также диаграммой рассеивания или корреляционным полем.
Пример 6.1. [10]
В результате комбинационной группировки 100 рабочих по общему стажу работы и месячной заработной плате получена следующая корреляционная таблица:
Группы рабочих по общему стажу работы (лет) |
Группы рабочих по размеру заработной платы (руб.) |
|
||||||
|
|
|
|
|
|
|
|
|
100-120 |
120-140 |
140-160 |
160-180 |
180-200 |
200-220 |
220-240 |
Итого |
|
0-5 |
5 |
6 |
14 |
7 |
|
|
|
32 |
5-10 |
|
3 |
4 |
7 |
10 |
2 |
|
26 |
10—15 |
|
1 |
2 |
6 |
5 |
4 |
|
18 |
15-20 |
|
|
|
4 |
1 |
6 |
1 |
12 |
20—25 |
|
|
|
1 |
3 |
1 |
3 |
8 |
25—30 |
|
|
|
|
1 |
2 |
1 |
4 |
Итого |
5 |
10 |
20 |
25 |
20 |
15 |
5 |
100 |
Для характеристики связи между рассматриваемыми показателями необходимо вычислить:
1) уравнение прямой регрессии между заработной платой и трудовым стажем рабочих;
2) коэффициент корреляции;
3) среднюю ошибку коэффициента корреляции.
Решение.
Обозначим общий производственный стаж рабочих через х, а их месячную заработную плату — через у. Тогда уравнение прямой регрессии между заработной платой и стажем рабочих будет:
![]() .
.
Для нахождения параметров этого уравнения необходимо решение следующей системы линейных уравнений:
![]()
Для выполнения вычислений составим расчетную таблицу:
y\x |
110 |
130 |
150 |
170 |
190 |
210 |
230 |
Итого |
2,5 |
275 1375 5 |
325 1950 6 |
375 5250 14 |
425 2975 7 |
|
|
|
11550 32 |
7,5 |
|
975 2925 3 |
1125 4500 4 |
1275 8925 7 |
1425 14250 10 |
1575 3150 2 |
|
33750 26 |
12,5 |
|
1625
1 |
1875 3750 2 |
2125 12750 6 |
2375 11875 5 |
2625 10500 4 |
|
40500 18 |
17,5 |
|
|
|
2975 11900 4 |
3325
1 |
3675 22050 6 |
4025
1 |
41300 12 |
22,5 |
|
|
|
3825
1 |
4275 12825 3 |
4725
1 |
5175 15525 3 |
36900 8 |
27,5 |
|
|
|
|
5225
1 |
5775 11550 2 |
6325
1 |
23100 4 |
Итого |
1375 5 |
6500 10 |
13500 20 |
40375 25 |
47500 20 |
51975 15 |
25875 5 |
187100 100 |
Замечание. В левом верхнем углу каждой клеточки таблицы показано произведение ху, в нижнем правом углу m — частота такого сочетания, в середине — произведение ху на частоту т (при значении частоты, равном единице, произведение ху=тху, и поэтому произведение тху не показывается).
Из этой таблицы определяется величина ∑тху, равная 187100. Для получения остальных величин, входящих в систему нормальных уравнений, составим расчетные таблицы, введя в них одновременно и величины, необходимые для расчета коэффициента корреляции. Произведем расчет вспомогательных величин по факторному признаку.
x |
2,5 |
7,5 |
12,5 |
17,5 |
22,5 |
27,5 |
Итого |
тх |
32 |
26 |
18 |
12 |
8 |
4 |
100 |
тх x |
80 |
195 |
225 |
210 |
180 |
110 |
1000 |
тхх2 |
200 |
1462,5 |
2812,5 |
3675 |
4050 |
3025 |
15225 |
Затем рассчитаем вспомогательные величины по результативному признаку:
y |
110 |
130 |
150 |
170 |
190 |
210 |
230 |
Итого |
ту |
5 |
10 |
20 |
25 |
20 |
15 |
5 |
100 |
ту y |
550 |
1310 |
3000 |
4250 |
3800 |
3150 |
1150 |
17200 |
ту y2 |
60500 |
169000 |
450000 |
722500 |
722000 |
661500 |
264500 |
3050000 |
Подставим найденные значения в систему уравнений и получим:
100а0+1000a1=17200;
1000а0+15225а1=187100.
В результате совместного решения уравнений находим: a0=143,1 и a1=2,89. Искомое уравнение прямой регрессии примет вид
![]() .
.
Это уравнение показывает, что между общим производственным стажем и заработной платой рабочих имеется прямая связь: с увеличением стажа на один год размер месячной заработной платы возрастает в среднем на 2р. 89к. (а1).
Коэффициент корреляции исчисляется по формуле:
![]()
Для нахождения значения знаменателя в формуле коэффициента корреляции вычислим среднее квадратическое отклонение величин факторного признака по формуле:
![]() где
где
![]() ,
,
а результативного — соответственно по формуле:
![]() где
где
![]() .
.
Подставим найденные величины в формулу коэффициента корреляции и получим:

Полученное значение коэффициента корреляции указывает на наличие достаточно тесной линейной связи между общим производственным стажем и заработной платой рабочих.
Если имеются равные интервалы отдельно по факторному и по результативному признакам, как, например, в данной задаче, нахождение коэффициента корреляции целесообразно производить с помощью следующей формулы:
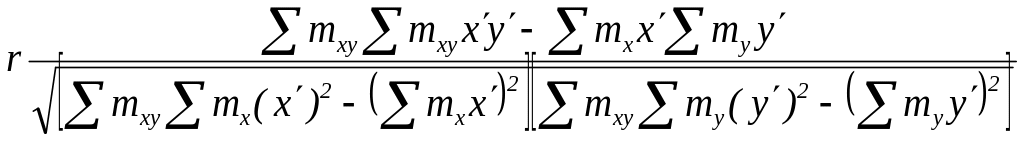 ,
,
где
![]() и
и
![]() условные варианты признаков при равных
интервалах;
условные варианты признаков при равных
интервалах;
тх, ту, и тху—частоты групп и подгрупп по х и у.
Так, для рассматриваемой задачи: х0=12,5, hх=5, y0=170 и hv = 20. Тогда корреляционная таблица будет иметь следующий вид:
|
-3 |
-2 |
-1 |
0 |
+1 |
+2 |
+3 |
mx |
mx x’ |
mx (x’)2 |
mxyx’y’ |
||||||
-2 |
6 30 5 |
4 24 6 |
2 28 14 |
7 |
|
|
|
32 |
-64 |
128 |
82 |
||||||
-1 |
|
2 6 3 |
1
4 |
7 |
-1
10 |
-2 -4 2 |
|
26 |
-26 |
26 |
-4 |
||||||
0 |
|
1 |
2 |
6 |
5 |
4 |
|
18 |
0 |
0 |
0 |
||||||
+1 |
|
|
|
4 |
1
1 |
2 12 6 |
3
1 |
12 |
12 |
12 |
16 |
||||||
+2 |
|
|
|
|
2 6 3 |
4
1 |
6 18 3 |
8 |
16 |
32 |
28 |
||||||
+3 |
|
|
|
|
3
1 |
6 12 2 |
9
1 |
4 |
12 |
36 |
24 |
||||||
my |
5 |
10 |
20 |
25 |
20 |
15 |
5 |
100 |
-50 |
234 |
146 |
||||||
туу' |
-15 |
-20 |
-20 |
0 |
20 |
30 |
15 |
10 |
|
||||||||
my(y’)2 |
45 |
40 |
20 |
0 |
20 |
60 |
45 |
230 |
|||||||||
Искомый коэффициент корреляции составит:

Средняя ошибка коэффициента корреляции определяется по формуле:
![]()
где r — коэффициент корреляции;
n — объем совокупности.
Подставим в эту формулу полученные данные:
![]()
Отношение коэффициента корреляции к его погрешности равно 13 (0,69:0,052), следовательно, можно считать, что полученный коэффициент корреляции достаточно точно выражает степень связи рассматриваемых показателей.
Коэффициент корреляции, уменьшенный на трехкратную величину погрешности, дает гарантийный минимум, а увеличенный на трехкратную величину погрешности — соответственно гарантийный максимум. Так, в данной задаче гарантийный минимум составляет 0,534-(0,69—3x0,052), а гарантийный максимум равен 0,846 (0,69+Зx0.052). Это означает, что для рассматриваемого примера можно ожидать, что не меньше 28,5% (0,534x0,534x100) вариации месячной заработной платы рабочих вызвано вариацией величины общего производственного стажа.
