Вариант 26
Для проведения градостроительных работ, вся территория изучаемого района была разделена на 50 сравнительно одинаковых районов и подсчитано количество жителей, проживающих в этих районах. Результаты опроса приведены ниже.
100 |
788 |
973 |
146 |
851 |
746 |
589 |
379 |
907 |
675 |
346 |
791 |
596 |
392 |
189 |
567 |
498 |
200 |
380 |
679 |
189 |
496 |
598 |
381 |
981 |
863 |
816 |
953 |
367 |
547 |
682 |
109 |
987 |
538 |
861 |
549 |
520 |
482 |
479 |
1000 |
927 |
486 |
952 |
927 |
912 |
827 |
765 |
549 |
290 |
1002 |
Построить вариационный ряд, гистограмму, полигон, кумуляту, огиву. Найти характеристики ряда и проверить гипотезу о нормальном распределении ряда.
При взвешивании некоторого груза получены следующие результаты (в граммах): 120; 125; 130; 121; 122; 120; 128. Определить среднеквадратическую ошибку и построить для нее доверительный интервал с надежностью 0,9.
Поверить гипотезу о нормальном распределении на основе данных ,приведенных в задаче № 1, используя различные критерии согласия.
Партия изделий принимается, если дисперсия контролируемого размера значимо не превышает 0,2. Исправленная выборочная дисперсия, найденная по выборке объема n = 121, оказалась равной
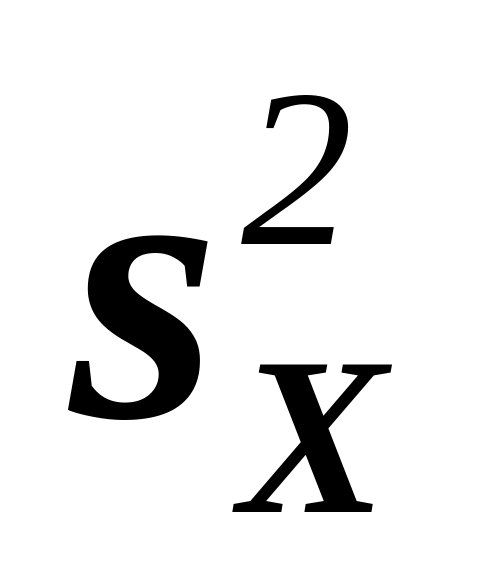=0,3.
Можно ли принять партию при уровне
значимости 0,05?Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
x y |
10 |
15 |
20 |
25 |
30 |
|
ny |
3 |
4 |
12 |
|
|
|
|
16 |
9 |
|
10 |
4 |
|
|
|
14 |
15 |
|
|
32 |
6 |
12 |
|
50 |
21 |
|
|
14 |
1 |
1 |
1 |
17 |
27 |
|
|
|
2 |
1 |
|
3 |
nx |
4 |
22 |
50 |
9 |
14 |
1 |
N=100 |