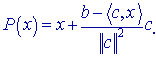4. Экстремальные свойства выпуклых функций.

Теорема 1.   Пусть f выпуклая функция на выпуклом множестве . Тогда всякая точкалокального минимума функцииf на множестве D является и точкой ее (глобального) минимума на множестве D.

Доказательство

Так как x^* - точка локального минимума функции f на множестве D, то существует такое, что

,

(1)

где . Предположим противное, то есть, что существует точкатакая, что

.

(2)

В силу выпуклости множества D, . Следовательнодля достаточно малых. В силу (1), (2) и в силу выпуклости функцииf на множестве D, для таких будем иметь. Полученное противоречие доказывает теорему.

Обозначим .

Теорема 2.   Пусть f - выпуклая функция на выпуклом множестве . ТогдаD^* - выпуклое множество.

Доказательство

Так как , то выпуклость множестваD^* следует из теорем 2.6 и 1.1.

Теорема 3.   Пусть f - строго выпуклая функция на выпуклом множестве . Тогда множествоD^* содержит не более чем одну точку. Доказательство

Пусть . Докажем, что оно состоит только из одной точки. Пусть это не так и существуют два вектораx^* и y^* принадлежащих множеству D^*. Тогда, в силу выпуклости множества D^* (см. предыдущую теорему), и, в силу строгой выпуклости функцииf, . Полученное противоречие доказывает теорему.

Теорема 4.   Пусть f - выпуклая и дифференцируемая функция на выпуклом множестве . Тогда для того, чтобы точкабыла точкой минимума функцииf на множестве D необходимо и достаточно, чтобы выполнялось неравенство

(1)

Доказательство

Необходимость. Пусть x^* - точка минимума функции f на множестве D. Предположим (1) не имеет места. Тогда существует точка такая, что. Поэтому, из теоремы 3.7 векторявляется направлением убывания функцииf в точке x^*. Следовательно, существует такое, что для любого, выполняется неравенство

.

(2)

В силу выпуклости множества D, . Тогда неравенство (2) припротиворечит тому, чтоx^* - точка минимума функции f на множестве D. Следовательно (1) имеет место. Достаточность. Пусть в точке в точке имеет место (1). Тогда из теоремы 3.1. Отсюда и из (1). Что и требовалось.

Следствие.   Пусть f - выпуклая и дифференцируемая на Eⁿ функция. Тогда для того, чтобы точка x^* была точкой безусловного минимума функции f необходимо и достаточно, чтобы f'(x^*)=0. Доказательство следует очевидным образом из приD =.

5. Проекция точки на множество

Определение 1   Проекцией точки на множествоназывается вектор, удовлетворяющий условию

(1)

Иногда проекцию точки x на множество D будем обозначать P( x, D)

Легко увидеть, что P( x ) = x

тогда и только тогда, когда

.

 

Задача (1) является задачей минимизации строго выпуклой неотрицательной функции на множестве . Часто нам удобнее будет иметь дело с эквивалентной ей задачей

(2)

Далеко не для всяких множеств D возможно найти точное решение этой задачи.

Теорема 1  Пусть D – замкнутое множество из , тогдаP( x )

существует для любого

.

Доказательство:

  Пусть z - произвольная точка из D. Обозначим

		. Очевидно, что
			, так как
				.    (3)

  Решение задачи (3) существует, так как множество D(z) - компактно,

а функция

непрерывна по y .

Нарушение условия теоремы 1 может привести к отсутствию проекции. Например D – открытое множество, а .

Теорема 2  Пусть D – выпуклое замкнутое множество из , тогда всякая точка имеет единственную проекцию на множествоD.

Доказательство:

  Существование проекции следует из предыдущей теоремы. Докажем

  единственность. Воспользуемся для отыскания проекции решением

задачи (2).

Так как функция

- строго выпуклая по y, то

  единственность ее минимума на выпуклом множестве D вытекает

  из теоремы 4.3,что и означает единственность проекции.

Нарушение условия выпуклости множества D в теореме 2 может привести к неоднозначности определения проекции.

Теорема 3  Для того, чтобы точка была проекцией точкина выпуклое замкнутое множество , необходимо и достаточно, чтобы выполнялось неравенство

(4)

Доказательство:

Для того, чтобы точка

была решением задачи (2) необходимо

  и достаточно, как следует из теоремы 4.4, чтобы выполнялось неравенство

				(5)
где
Так как		и			, то условия

(5) и (4) эквивалентны. Что и требовалось.

Задача отыскания проекции точки на выпуклое множество – это задача минимизации выпуклой функции на выпуклом множестве, решать которые мы только лишь учимся. Необходимо заметить, что, как правило, отыскать точно проекцию точки невозможно. Поэтому приходится пользоваться процедурами для нахождения приближенных значений проекции. Однако, при достаточно "простых" множествах D проекцию можно вычислить, пользуясь достаточно простыми "явными" формулами. Приведем несколько примеров таких множеств.

 

1. Неотрицательный ортант:					Обозначим
j-ую  координату вектора P( x )		. Тогда		j=1,…,n.

2. n-мерный параллелепипед:

j=1,…,n.

3. Шар радиуса r c центром в 0:

4. Гиперплоскость:

где

5. Полупространство:

6. Линейное многообразие:

где A - матрица размерности m  n