3. Дифференциальные свойства выпуклых функций.

Теорема 1.   Пусть открытое множество,выпуклое множество, функцияf определена и дифференцируема на множестве G. Тогда для того, чтобы f, была выпуклой на множестве D функцией, необходимо и достаточно, чтобы выполнялось неравенство

, .

(1)

Доказательство

Необходимость. Пусть функция f-выпуклая на D, и. В силу выпуклости функцииf справедливо неравенство . Откуда. Переходя к пределу, в этом неравенстве, при, получим (1).Достаточность. Пусть имеет место (1), ,. Положим. Из (1) имеем

,	(2)
.	(3)

Умножая (2) на t, (3) на (1-t) и складывая эти неравенства, получим . Откуда, что и означает выпуклость функцииf на D.

Теорема 2.   Пусть открытое множество,выпуклое множество, функцияf определена и дифференцируема на множестве G. Тогда для того, чтобы f, была выпуклой на множестве D функцией, необходимо и достаточно, чтобы выполнялось неравенство

, .

(4)

Доказательство

Необходимость. Пусть функция f - выпуклая на D, . В силу теоремы 1 имеют место неравенстваи. Сложив эти неравенства, получим (4).Достаточность. Пусть имеет место (4), ,. Положим. Применяя формулу Лагранжа (конечных приращений), получим,, где. Умножая первое равенство наt, а второе на (1-t), складывая их и используя (4), получим , где,,. откуда, что и означает выпуклость функцииf на D.

Теорема 3.   Пусть функция f определена и дважды дифференцируема на . Тогда для того, чтобыf была выпуклой функцией, необходимо и достаточно, чтобы матрица f"(x) была неотрицательно определена на .

Доказательство

Пусть . Применяя формулу конечных приращений из неравенства (4), получим

,

(5)

где . Из теоремы 2 неравенство (4) - необходимо и достаточно для выпуклости функцииf, следовательно неравенство (5) также необходимо и достаточно для выпуклости функции f. А (5) и означает неотрицительную определенность матрицы f"(x) на .

Заметим, что критерием вогнутости функции является неположительная определенность матрицы f"(x), критерием строгой выпуклости является положительная определенность матрицы f"(x), а строгой вогнутости- отрицательная определенность. Известен критерий выпуклости дважды дифференцируемых функций и в более общей нежели в теореме 3 форме.   Теорема 3 очень удобна для установления выпуклости функций. Теоремы 1-3 особенно просто и удобно формулируются в одномерном случае и имеют наглядный геометрический смысл. Пусть функция f определена на ,. Определим следующую функцию одной переменной.

Теорема 4.   Функция f, определенная на , является выпуклой, тогда и только тогда, когда выпуклой является и функциядля любых.

Доказательство

Необходимость. Пусть f - выпуклая функция, . Выберем произвольно. Тогда. Таким образом,- выпуклая функция.Достаточность. Пусть для произвольных функция- выпуклая. Выберем произвольнои. Тогда. Что и требовалось доказать.

Неравенство (1) из теоремы 1 в одномерном случае имеет вид

, .

(6)

Если , неравенство (6) перепишем в виде.

Геометрическая иллюстрация неравенства 6.  

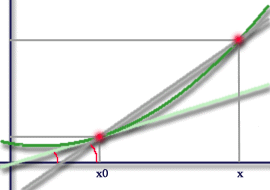
Неравенство (4) из теоремы 2 в одномерном случае имеет вид ,, что равносильно монотонности функции. Таким образом, справедлива

Теорема 5.   Пусть - дифференцируемая функция. Тогда, для того, чтобы она была выпуклой необходимо и достаточно, чтобыбыла неубывающей наR. Из теоремы 3 для одномерного случая вытекает следующая Теорема 6.   Пусть - дважды дифференцируемая функция. Тогда для того, чтобы она была выпуклой необходимо и достаточно, чтобынаR. Определение 1.   Пусть f - функция, определенная на . Векторназываетсянаправлением убывания функциии f в точке , если существует числотакое, что для любого, выполняется неравенство.Теорема 7.   Пусть f - выпуклая дифференцируемая на функция,. Для того, чтобы векторбыл направлением убывания функцииf в точке x, необходимо и достаточно чтобы выполнялось неравенство

(7)

Доказательство

Необходимость. Пусть s - направление убывания функции f в точке x. Тогда существует такое, что,. Из теоремы 1 следует,. Из этих двух неравенств следует (7).Достаточность. Пусть имеет место (7). Так как функция f дифференцируема, то , где. Поэтому, для достаточно малыхt, знак приращения функции f совпадает со знаком . Тогда из (7) следует, что существуеттакое, что,. Что и требовалось.