Переструктурированные результаты Таблица 15
Ранг 1 замера |
Ранг 2 замера |
P количество совпадений |
Q количество расхождений |
||
1 |
3 |
7 |
2 |
||
2 |
2 |
7 |
1 |
||
3 |
1 |
7 |
0 |
||
4 |
6 |
4 |
2 |
||
5 |
4 |
5 |
0 |
||
6 |
5 |
4 |
0 |
||
7 |
10 |
0 |
3 |
||
8 |
9 |
0 |
2 |
||
9 |
8 |
0 |
1 |
||
10 |
7 |
0 |
0 |
||
Σ |
34 |
11 |
|||
Помимо рангов в этой таблице есть также информация о совпадениях и расхождениях. Рассмотрим их подробнее понятия совпадения и расхождения.
Если два замера будут иметь одинаковые ранги у всех участников исследования, то совпадения окажется полным – с возрастанием одного ранга будет возрастать и другой. Если же два результата двух замеров частично соответствуют друг другу, то уровень соответствия и покажет число совпадений, то есть показатель соответствия увеличения одних рангов вслед за увеличением других.
Расхождения, в свою очередь, имеют противоположное значение – это показатель того, как с увеличением рангов 1 замера ранги второго замера уменьшаются.
Определяются значения совпадений и расхождений по каждому рангу второго замера. Рассмотрим самый первый ранг этого замера – ранг 3. Определим, сколько ниже этого ранга (при определении совпадений и расхождений используется только столбец рангов второго замера) расположено значений, превышающих 3. Таких значений 7 (это ранги 6, 4, 5, 10, 9, 8, и 7). Поэтому в столбце совпадений в соответствующей строчке указываем 7. Затем считаем количество рангов, меньших 3. Таких рангов 2 (это значения 2 и 1). Соответственно, в столбике расхождений мы указываем 2. После этого переходим к следующему рангу 2 замера – рангу 2. Ниже его расположено также 7 рангов, превышающих рассматриваемое значение. Вносим цифру 7 в столбец совпадений. В столбце расхождений указываем 1, так как единственное значение (ранг 1) меньше рассматриваемого ранга 2. У следующего ранга (это ранг 1) ниже находятся 7 значений, превышающих его и нет ни одного значения меньше. У ранга 6 следующего по расположению) числу совпадений 4 (это ранги 10, 9, 8 и 7) и количество расхождений 2 (ранги 4 и 5). Таким образом подсчитывается для каждого ранга 2 замера число совпадений и расхождений. После того как все значения определены, находится итоговое, суммарное значение расхождений. В нашем примере суммарное значение P (совпадений) равно 34. Суммарное значение Q (расхождений) равно 11. Найденные значения P и Q представляем в расчетную формулу и находим значения коэффициента корреляции:
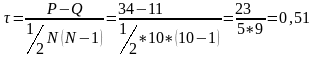
Полученное расчетное значение коэффициента корреляции Кендалла меньше расчетного значения, полученного с помощью коэффициента корреляции Спирмена. В данном модуле мы не будем определять значимость полученного коэффициента корреляции. Эта возможность рассматривается в следующем параграфе с опорой на статистические программы.