Как построить плоскость, параллельную данной?

Пример 8

Построить плоскость, проходящую через точку   параллельно плоскости  .

Решение: Обозначим известную плоскость через  . По условию требуется найти плоскость  , которая параллельна плоскости   и проходит через точку  .

Выполним схематический чертёж, который поможет быстрее разобраться в условии и понять алгоритм решения: 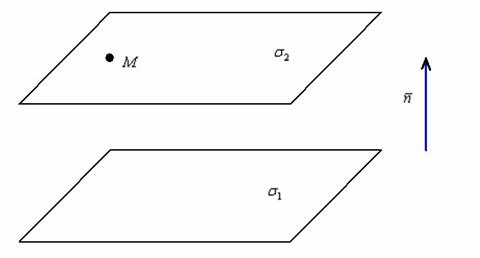У параллельных плоскостей один и тот же вектор нормали. Добавить нечего =) Осталось оформить мат в два хода:

1) Из уравнения   найдём вектор нормали плоскости:  .

2) Уравнение плоскости   составим по точке   и вектору нормали  :

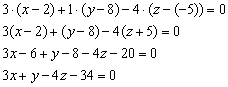
Ответ: 

Как выполнить проверку, я уже рассказал.

Продолжаем раскидывать стог сена пространственной геометрии:

Как найти расстояние от точки до плоскости?

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки   к данной плоскости: 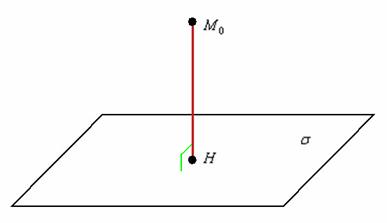При необходимости можно найти и точку  , но для этого необходимо разобраться суравнениями прямой в пространстве и посетить урок Основные задачи на прямую и плоскость.

Формула очень похожа на формулу «плоской» геометрии расстояния от точки до прямой (см. Пример №8 урока Простейшие задачи с прямой на плоскости).

Расстояние от точки   до плоскости   выражается формулой 

Пример 9

Найти расстояние от точки   до плоскости 

Решение: анализировать тут нечего, главное, не допустить ошибку в вычислениях:

Ответ: 

Такое даже для самостоятельного решения неловко предлагать.

Заключительный раздел урока будет посвящен взаимному расположению плоскостей. Мы уже немного поговорили о параллельных плоскостях, и сейчас продолжим тему:

Взаимное расположение плоскостей

Для практики наиболее важна информация о взаимном расположении двух плоскостей, но и о трёх плоскостях также будет краткая справка.

Рассмотрим две плоскости пространства, заданные общими уравнениями: 

Они могут:

1) совпадать;

2) быть параллельными:  ;

3) пересекаться по некоторой прямой «эль»:  .

Всё очень и очень похоже на взаимное расположение прямых на плоскости (урокПростейшие задачи с прямой на плоскости).

Совпадающие плоскости

Две плоскости совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства 

Рассмотрим плоскости   и составим систему:

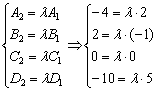
Из каждого уравнения системы следует, что  . Таким образом, система совместна и плоскости   совпадают.

Параллельные плоскости

Две плоскости параллельны тогда и только тогда, когда их коэффициенты при переменных    пропорциональны:  , но  .

На практике очень часто первые три коэффициента банально совпадают ( ). Посмотрим, например, на уравнения параллельных плоскостей из Примера №8:

Комментарии, думаю, излишни, всё прекрасно видно. Но на всякий случай выполню формальную проверку, вдруг кому потребуется. Составим систему:

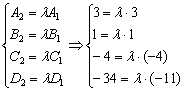
Из первых трёх уравнений следует, что  , а из четвёртого уравнения следует, что  , значит, система несовместна. Но коэффициенты при переменных   пропорциональны, следовательно, плоскости параллельны.

Задача о построении параллельной плоскости уже была, поэтому решим что-нибудь новое: