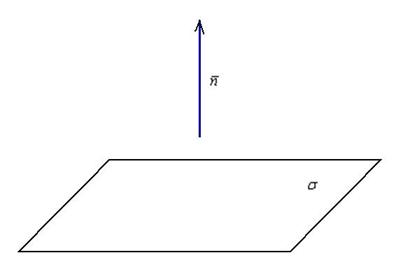
Вектор нормали плоскости (нормальный вектор)
Вектор
нормали плоскости – это вектор, который
перпендикулярен данной плоскости.
Очевидно, что у любой плоскости бесконечно
много нормальных векторов. Но для решения
задач нам будет хватать и одного.
Если
плоскость задана общим уравнением
,
то вектор 
является вектором нормали данной
плоскости.
Просто до безобразия. Всё, что нужно
сделать – это «снять» коэффициенты из
уравнения плоскости.
Обещанного
три экрана ждут, вернёмся к Примеру №1
и выполним его проверку. Напоминаю, что
там требовалось построить уравнение
плоскости по точке
и
двум векторам 
.
В результате решения мы получили
уравнение
.
Проверяем:
Во-первых,
подставим координаты точки
в
полученное уравнение:
Получено
верное равенство, значит, точка 
действительно
лежит в данной плоскости.
Во-вторых,
из уравнения плоскости снимаем вектор
нормали: 
.
Поскольку векторы
параллельны
плоскости, а вектор 
перпендикулярен
плоскости, то должны иметь место следующие
факты: 
.
Перпендикулярность векторов легко
проверить с помощью скалярного
произведения:
Вывод: уравнение плоскости найдено правильно.
В
ходе проверки я фактически процитировал
следующее утверждение теории: вектор 
параллелен
плоскости
в
том и только том случае, когда 
.
Решим важную задачу, которая имеет отношение и к уроку Скалярное произведение векторов:
Пример 5
Найти
единичный нормальный вектор плоскости 
.
Решение:
Единичный вектор – это вектор, длина
которого равна единице. Обозначим данный
вектор через 
.
Принципиально пейзаж выглядит
так:
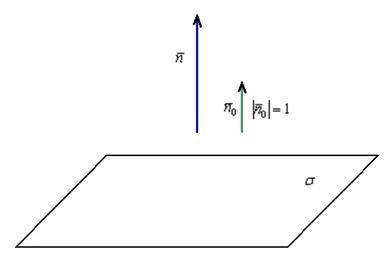Совершенно
понятно, что векторы 
коллинеарны.
Сначала
из уравнения плоскости снимем вектор
нормали: 
.
Как
найти единичный вектор? Для
того чтобы найти единичный вектор
,
нужнокаждую координату
вектора 
разделить
на длину вектора 
.
Перепишем
вектор нормали в виде 
и
найдём его длину:
Согласно
вышесказанному:
Ответ: 
Проверка: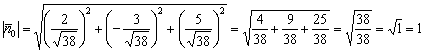 
,
что и требовалось проверить.
Читатели,
которые внимательно изучили последний
параграф урока Скалярное
произведение векторов,
наверное, заметили, что координаты
единичного вектора 
–
это в точности направляющие косинусы
вектора
:
Отвлечёмся от разобранной задачи: когда вам дан произвольный ненулевой вектор, и по условию требуется найти его направляющие косинусы (последние задачи урока Скалярное произведение векторов), то вы, по сути, находите и единичный вектор, коллинеарный данному.
Фактически два задания в одном флаконе.
Необходимость найти единичный вектор нормали возникает в некоторых задачах математического анализа.
С выуживанием нормального вектора разобрались, теперь ответим на противоположный вопрос:
Как составить уравнение плоскости по точке и вектору нормали?
Эту жёсткую конструкцию вектора нормали и точки хорошо знает мишень для игры в дартс. Пожалуйста, вытяните руку вперёд и мысленно выберите произвольную точку пространства, например, маленькую кошечку в серванте. Очевидно, что через данную точку можно провести единственную плоскость, перпендикулярную вашей руке.
Уравнение
плоскости, проходящей через
точку
перпендикулярно
вектору 
,
выражается формулой:
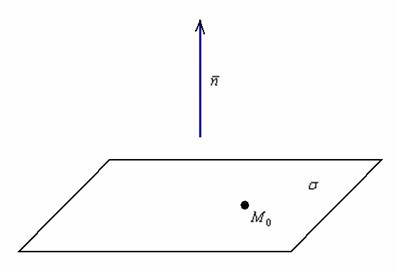Выглядит
значительно привлекательнее, чем
предыдущие мытарства. В некоторых
задачах аналитической геометрии
уравнение плоскости можно составить
несколькими способами, и решение через
точку и нормальный вектор – самое
оптимальное.
Пример 6
Составить
уравнение плоскости по точке 
и
вектору нормали 
.
Решение:
Используем формулу:
Ответ: 
Проверка выполняется очень легко:
1)
Из полученного уравнения 
снимаем
вектор нормали: 
–
всё хорошо, полученный вектор совпал с
вектором из условия (в ряде случаев
может получиться коллинеарный вектор).
2)
Подставим координаты точки 
в
уравнение плоскости:
Верное
равенство, значит, точка
принадлежит
данной плоскости.
Вывод: уравнение плоскости найдено правильно.
Пример настолько прозрачен, что хочется немного завуалировать условие:
Пример 7
Найти
уравнение плоскости, проходящей через
точку 
перпендикулярно
оси
.
Это пример для самостоятельного решения. Просто, но со вкусом.
Перейдём к более содержательным примерам. Типовая задача: