Перпендикулярные прямые. Расстояние от точки до прямой. Угол между прямыми

Начнём с типовой и очень важной задачи. В первой части мы узнали, как построить прямую, параллельную данной, а сейчас избушка на курьих ножках развернётся на 90 градусов:

Как построить прямую, перпендикулярную данной?

Пример 6

Прямая задана уравнением  . Составить уравнение перпендикулярной прямой  , проходящей через точку  .

Решение: По условию известно, что  . Неплохо бы найти направляющий вектор прямой  . Поскольку прямые перпендикулярны, фокус прост:

Из уравнения   «снимаем» вектор нормали:  , который и будет направляющим вектором прямой  .

Уравнение прямой   составим по точке   и направляющему вектору  :

Ответ: 

Развернём геометрический этюд:

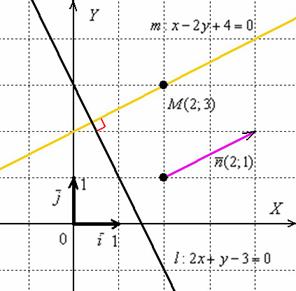
М-да… Оранжевое небо, оранжевое море, оранжевый верблюд.

Аналитическая проверка решения:

1) Из уравнений   вытаскиваем направляющие векторы   и с помощью скалярного произведения векторов приходим к выводу, что прямые действительно перпендикулярны:  .

Кстати, можно использовать векторы нормали, это даже проще.

2) Проверяем, удовлетворяет ли точка   полученному уравнению  .

Проверку, опять же, легко выполнить устно.

Пример 7

Найти точку пересечения перпендикулярных прямых  , если известно уравнение   и точка  .

Это пример для самостоятельного решения. В задаче несколько действий, поэтому решение удобно оформить по пунктам.

Наше увлекательное путешествие продолжается:

Расстояние от точки до прямой

Перед нами прямая полоса реки и наша задача состоит в том, чтобы дойти до неё кратчайшим путём. Препятствий нет, и самым оптимальным маршрутом будет движение по перпендикуляру. То есть, расстояние от точки до прямой – это длина перпендикулярного отрезка.

Расстояние в геометрии традиционно обозначают греческой буквой «ро», например:   – расстояние от точки «эм» до прямой «дэ».

Расстояние от точки   до прямой   выражается формулой 

Пример 8

Найти расстояние от точки   до прямой 

Решение: всё что нужно, это аккуратно подставить числа в формулу и провести вычисления:

Ответ: 

Выполним чертёж: 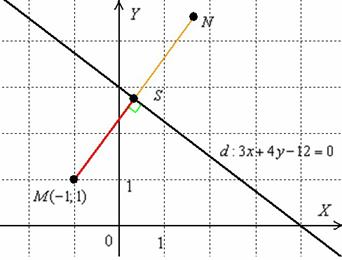Найденное расстояние от точки до прямой – это в точности длина красного отрезка. Если оформить чертёж на клетчатой бумаге в масштабе 1 ед.  = 1 см (2 клетки), то расстояние можно измерить обыкновенной линейкой.

Рассмотрим ещё одно задание по этому же чертежу:

Как построить точку, симметричную относительно прямой?

Задача состоит в том, чтобы найти координаты точки  , которая симметрична точке   относительно прямой  . Предлагаю выполнить действия самостоятельно, однако обозначу алгоритм решения с промежуточными результатами:

1) Находим прямую  , которая перпендикулярна прямой  .

2) Находим точку пересечения прямых:  .

Оба действия подробно разобраны в рамках данного урока.

3) Точка   является серединой отрезка  . Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим  .

Не лишним будет проверить, что расстояние   тоже равно 2,2 единицам.

Трудности здесь могут возникнуть в вычислениях, но в вышке здорово выручает микрокалькулятор, позволяющий считать обыкновенные дроби. Неоднократно советовал, посоветую и снова.