Доказать, что 3 вектора образуют базис трёхмерного пространства и найти координаты 4-го вектора в данном базисе

Пример 8

Даны векторы  . Показать, что векторы   образуют базис трехмерного пространства и найти координаты вектора   в этом базисе.

Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора   вполне могут образовывать новый базис. И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы   линейно независимы:

Вычислим определитель, составленный из координат векторов  : , значит, векторы   линейно независимы и образуют базис трехмерного пространства.

! Важно: координаты векторов   обязательно записываем в столбцыопределителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.

Теперь вспомним теоретическую часть: если векторы   образуют базис, то любой вектор   можно единственным способом разложить по данному базису:  , где   – координаты вектора  в базисе  .

Поскольку наши векторы   образуют базис трёхмерного пространства (это уже доказано), то вектор   можно единственным образом разложить по данному базису: , где   – координаты вектора   в базисе  .

По условию и требуется найти координаты  .

Для удобства объяснения поменяю части местами:  . В целях нахождения   следует расписать данное равенство покоординатно:

По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя  , в правую часть записаны координаты вектора  .

Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают поформулам Крамера, часто даже в условии задачи есть такое требование.

Главный определитель системы уже найден: , значит, система имеет единственное решение.

Дальнейшее – дело техники:

Таким образом:  – разложение вектора   по базису  .

Ответ: 

Как я уже отмечал, задача носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, абстрактные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу, решение будет намного проще. Однако на практике мне такое задание ни разу не встречалось, именно поэтому я его пропустил в предыдущем разделе.

Такая же задача с трёхмерными векторами для самостоятельного решения:

Пример 9

Даны векторы  . Показать, что векторы   образуют базис и найти координаты вектора   в этом базисе. Систему линейных уравнений решить методом Крамера.

Полное решение и примерный образец чистового оформления в конце урока.

Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра. Собственно, о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.

Любите векторы, и векторы полюбят вас!

Решения и ответы:

Пример 2: Решение: составим пропорцию из соответствующих координат векторов: Ответ: при 

Пример 4: Доказательство: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. 1) Проверим параллельность противоположных сторон   и  . Найдём векторы: 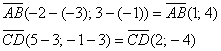Вычислим определитель, составленный из координат векторов  : , значит, данные векторы не коллинеарны, и стороны   не параллельны. 2) Проверим параллельность противоположных сторон   и  . Найдём векторы: 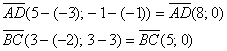Вычислим определитель, составленный из координат векторов  : , значит, данные векторы  коллинеарны, и  . Вывод: Две стороны четырёхугольника   параллельны, а две другие стороны не параллельны, значит, он является трапецией по определению. Что и требовалось доказать.

Пример 5: Решение:  б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов: Система не имеет решения, значит, векторы   не коллинеарны. Более простое оформление:   – вторая и третья координаты не пропорциональны, значит, векторы   не коллинеарны. Ответ: векторы   не коллинеарны. в) Исследуем на коллинеарность векторы  . Составим систему: Соответствующие координаты векторов пропорциональны, значит  Вот здесь как раз не проходит «пижонский» метод оформления.  Ответ: 

Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов   (определитель раскрыт по первой строке):   , значит, векторы   линейно зависимы и не образуют базиса трёхмерного пространства. Ответ: данные векторы не образуют базиса

Пример 9: Решение: Вычислим определитель, составленный из координат векторов  : Таким образом, векторы   линейно независимы и образуют базис. Представим вектор   в виде линейной комбинации базисных векторов: Покоординатно: Систему решим по формулам Крамера: , значит, система имеет единственное решение.

Ответ: Векторы   образуют базис, 

Автор: Емелин Александр