Как определить коллинеарность векторов пространства?

Правило очень похоже. Для того чтобы два вектора пространства   были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны  .

Пример 5

Выяснить, будут ли коллинеарны следующие векторы пространства:

а)  ; б)  в) 

Решение: а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:

Система не имеет решения, значит, векторы   не коллинеарны.

«Упрощёнка» оформляется проверкой пропорции  . В данном случае:  – соответствующие координаты не пропорциональны, значит, векторы   не коллинеарны.

Ответ: векторы   не коллинеарны.

б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.

Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов.

Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.

Добро пожаловать во второй раздел:

Линейная зависимость и независимость векторов трехмерного пространства. Пространственный базис и аффинная система координат

Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.

Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.

И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы  , они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов! Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)

Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства?  Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являютсякомпланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.

Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).

Определение: три вектора называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.

Компланарные векторы всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы   мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы   не коллинеарны, то третий вектор выражается через них единственным образом:   (а почему – легко догадаться по материалам предыдущего раздела).

Справедливо и обратное утверждение: некомпланарные векторы всегда линейно независимы, то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.

Определение: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов  , взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису  , где   – координаты вектора   в данном базисе

Напоминаю, также можно сказать, что вектор   представлен в виде линейной комбинациибазисных векторов.

Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:

Точка   пространства, которая называется началом координат, и  некомпланарныевекторы  , взятые в определённом порядке,  задают аффинную систему координат трёхмерного пространства:

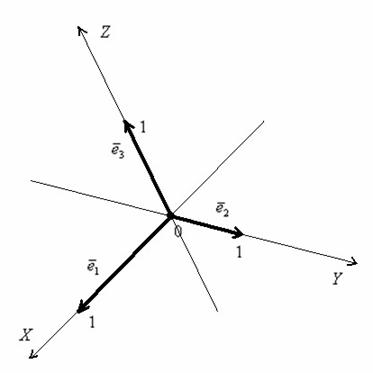
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная  система координат позволяет нам однозначно определить координаты любого вектора и координатной любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.

Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства:

Точка   пространства, которая называется началом координат, и ортонормированныйбазис   задают декартову прямоугольную систему координат пространства. Знакомая картинка:

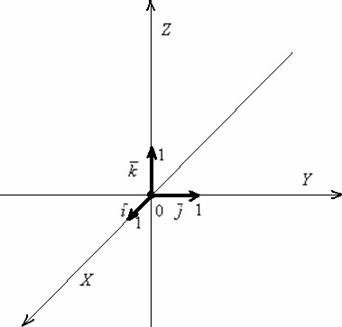
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:

Для трёх векторов пространства эквиваленты следующие утверждения: 1) векторы линейно независимы; 2) векторы образуют базис; 3) векторы не компланарны; 4) векторы нельзя линейно выразить друг через друга; 5) определитель, составленный из координат данных векторов, отличен от нуля.

Противоположные высказывания, думаю, понятны.

Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5). Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:

Три вектора пространства   компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю:  .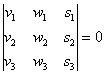

Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.

Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?

Пример 6

Проверить, образуют ли базис трёхмерного пространства следующие векторы:

а)  б) 

Решение: Фактически всё решение сводится к вычислению определителя.

а) Вычислим определитель, составленный из координат векторов   (определитель раскрыт по первой строке):   , значит, векторы   линейно независимы (не компланарны) и образуют базис трёхмерного пространства.

Ответ: данные векторы образуют базис

б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.

Встречаются и творческие задачи:

Пример 7

При каком значении параметра   векторы   будут компланарны?

Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:

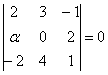
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от от минусов:

Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:

Ответ: при 

Здесь легко выполнить проверку, для этого нужно подставить полученное значение   в исходный определитель и убедиться, что  , раскрыв его заново.

В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика: