Как определить коллинеарность векторов плоскости?
Типовая
вещь. Для
того чтобы два вектора плоскости 
были
коллинеарны, необходимо и достаточно,
чтобы их соответствующие координаты
были пропорциональны 
. По
существу, это покоординатная детализация
очевидного соотношения 
.
Пример 1
а)
Проверить, коллинеарны ли векторы 
.
б)
Образуют ли базис векторы 
?
Решение:
а)
Выясним, существует ли для
векторов
коэффициент
пропорциональности
,
такой, чтобы выполнялись равенства
:
,
значит, данные векторы коллинеарны.
Обязательно
расскажу о «пижонской» разновидности
применения данного правила, которая
вполне прокатывает на практике. Идея
состоит в том, чтобы сразу составить
пропорцию 
и
посмотреть, будет ли она верной:
Составим
пропорцию из отношений соответствующих
координат векторов:
Сокращаем:
,
таким образом, соответствующие координаты
пропорциональны, следовательно,
Отношение
можно было составить и наоборот, это
равноценный вариант:
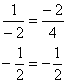
Для
самопроверки можно использовать то
обстоятельство, что коллинеарные векторы
линейно выражаются друг через друга. В
данном случае имеют место равенства 
.
Их справедливость легко проверяется
через элементарные действия с векторами:
б)
Два вектора плоскости образуют базис,
если они не коллинеарны (линейно
независимы). Исследуем на коллинеарность
векторы
.
Составим систему:
Из
первого уравнения следует, что 
,
из второго уравнения следует, что 
,
значит,система
несовместна (решений
нет). Таким образом, соответствующие
координаты векторов не пропорциональны.
Вывод: векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим
пропорцию из соответствующих координат
векторов
:
,
значит, данные векторы линейно независимы
и образуют базис.
Обычно
такой вариант не бракуют рецензенты,
но возникает проблема в тех случаях,
когда некоторые координаты равны нулю.
Вот так: 
.
Или так: 
.
Или так: 
.
Как тут действовать через пропорцию?
(действительно, на ноль же делить нельзя).
Именно по этой причине я и назвал
упрощенное решение «пижонским».
Ответ: а) 
,
б) образуют.
Небольшой творческий пример для самостоятельного решения:
Пример 2
При
каком значении параметра
векторы 
будут
коллинеарны?
В образце решения параметр найден через пропорцию .
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквиваленты следующие утверждения: 1) векторы линейно независимы; 2) векторы образуют базис; 3) векторы не коллинеарны; 4) векторы нельзя линейно выразить друг через друга; + 5) определитель, составленный из координат данных векторов, отличен от нуля.
Соответственно, эквивалентны следующие противоположные утверждения: 1) векторы линейно зависимы; 2) векторы не образуют базиса; 3) векторы коллинеарны; 4) векторы можно линейно выразить друг через друга; + 5) определитель, составленный из координат данных векторов, равен нулю.
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим
более подробно новый, пятый пункт: два
вектора плоскости
коллинеарны
тогда и только тогда, когда определитель,
составленный из координат данных
векторов, равен нулю: 
.
Для применения данного признака,
естественно, нужно уметь находить
определители.
Решим Пример 1 вторым способом:
а)
Вычислим определитель, составленный
из координат векторов
:
,
значит, данные векторы коллинеарны.
б)
Два вектора плоскости образуют базис,
если они не коллинеарны (линейно
независимы). Вычислим определитель,
составленный из координат векторов
:
,
значит, векторы 
линейно
независимы и образуют базис.
Ответ: а) , б) образуют.
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
Проверка векторов на коллинеарность – простая и очень распространенная задача аналитической геометрии. Нередко в условии заодно требуется проверить векторы и на ортогональность (базис в таких случаях, как правило, ортонормированный). Данное задание подробно рассмотрено на уроке Скалярное произведение векторов.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Пример 3
Даны
вершины четырёхугольника 
.
Доказать, что четырёхугольник 
является
параллелограммом.
Доказательство: Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма: Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким
образом, необходимо доказать:
1)
параллельность противоположных
сторон
и 
;
2)
параллельность противоположных
сторон 
и 
.
Доказываем:
1)
Найдём векторы:
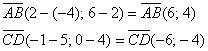
Вычислим
определитель, составленный из координат
векторов 
:
,
значит, данные векторы коллинеарны,
и 
.
2)
Найдём векторы:
Получился
один и тот же вектор («по школьному» –
равные векторы). Коллинеарность совсем
очевидна, но решение таки лучше оформить
с толком, с расстановкой. Вычислим
определитель, составленный из координат
векторов 
:
,
значит, данные векторы коллинеарны,
и 
.
Вывод: Противоположные стороны четырёхугольника попарно параллельны, значит, он является параллелограммом по определению. Что и требовалось доказать.
Больше фигур хороших и разных:
Пример 4
Даны
вершины четырёхугольника 
.
Доказать, что четырёхугольник
является
трапецией.
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство: