Скалярное произведение в координатах, если векторы заданы суммами векторов
Пример 13
Найти
скалярное произведение векторов 
,
если 
Решение: Напрашивается
трафаретное решение предыдущего раздела,
где мы составляли произведение и
раскрывали скобки: 
.
Но сейчас нам неизвестны длины векторов
и
угол между ними. Зато известны координаты.
Решение на самом деле будет очень
простым:
Найдём
вектор
:
Найдём
вектор
:
Проделаны
элементарные действия с векторами,
которые рассмотрены в конце урокаВекторы
для чайников.
Вычислим
скалярное произведение:
Ответ: 
Что и говорить, иметь дело с координатами значительно приятнее.
Пример 14
Найти
скалярное произведение векторов 
и 
,
если 
Это
пример для самостоятельного решения.
Здесь можно использовать ассоциативность
операции, то есть не считать 
,
а сразу вынести тройку за пределы
скалярного произведения и домножить
на неё в последнюю очередь. Решение и
ответ в конце урока.
В заключение параграфа провокационный пример на вычисление длины вектора:
Пример 15
Найти
длины векторов 
,
если 
Решение: Снова
напрашивается путь из предыдущего
раздела: 
,
и опять мы не знаем длин векторов и угла
между ними. Решение элементарно:
Найдём
вектор
:
И
его длину по тривиальной формуле
:
Скалярное произведение здесь вообще не при делах!
Как
не при делах оно и при вычислении длины
вектора 
:
Стоп.
А не воспользоваться ли очевидным
свойством длины вектора? Что можно
сказать о длине вектора 
?
Данный вектор длиннее вектора
в
5 раз. Направление противоположно, но
это не играет роли, ведь разговор о
длине. Очевидно, что длина вектора 
равна
произведению модуля числа
на
длину вектора
:
–
знак модуля «съедает» возможный минус
числа
.
Таким
образом:
Ответ: 
Формула косинуса угла между векторами, которые заданы координатами
Теперь
у нас есть полная информация, чтобы
ранее выведенную формулу косинуса угла
между векторами 
выразить
через координаты векторов 
:
Косинус
угла между векторами плоскости
и 
,
заданными в ортонормированном
базисе
, выражается
формулой:
.
Косинус
угла между векторами пространства
,
заданными в ортонормированном
базисе
, выражается
формулой:
Пример 16
Даны
три вершины треугольника 
.
Найти 
(угол
при вершине
).
Решение: По
условию чертёж выполнять не требуется,
но всё-таки:
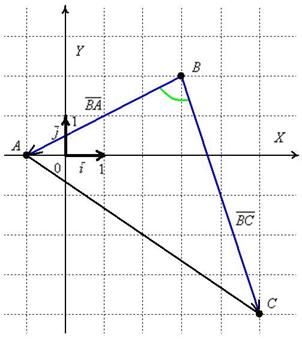Требуемый
угол
помечен
зелёной дугой. Сразу вспоминаем школьное
обозначение угла:
–
особое внимание на среднюю букву
–
это и есть нужная нам вершина угла. Для
краткости можно было также записать
просто 
.
Из
чертежа совершенно очевидно, что
угол
треугольника
совпадает с углом между векторами
и
,
иными словами: 
.
Проведённый анализ желательно научиться выполнять мысленно.
Найдём
векторы:
Вычислим
скалярное произведение:
И
длины векторов:
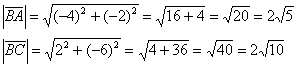
Косинус
угла:
Именно
такой порядок выполнения задания
рекомендую чайникам. Более подготовленные
читатели могут записывать вычисления
«одной строкой»:
Вот и пример «плохого» значения косинуса. Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём
сам угол:
Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки угол также можно измерить и транспортиром. Не повредите покрытие монитора =)
Ответ: 
В
ответе не забываем, что спрашивалось
про угол треугольника (а
не про угол между векторами), не забываем
указать точный ответ: 
и
приближенное значение угла: 
,
найденное с помощью калькулятора.
Те,
кто получил удовольствие от процесса,
могут вычислить углы 
,
и убедиться в справедливости канонического
равенства 
Пример 17
В
пространстве задан треугольник
координатами своих вершин 
.
Найти угол между сторонами 
и 
Это пример для самостоятельного решения. Полное решение и ответ в конце урока
Небольшой заключительный раздел будет посвящен проекциям, в которых тоже «замешано» скалярное произведение: