Скалярное произведение в координатах

Скалярное произведение векторов   и  , заданных в ортонормированном базисе  , выражается формулой 

Скалярное произведение векторов  , заданных в ортонормированном базисе  , выражается формулой 

То есть, скалярное произведение равно сумме произведений соответствующих координат векторов.

Пример 8

Найти скалярное произведение векторов: а)   и  б)   и  , если даны точки 

Решение:  а) Здесь даны векторы плоскости. По формуле  :

К слову: скалярное произведение получилось отрицательным, значит, угол между данными векторами является тупым. Пытливые умы могут отложить на плоскости векторы   от одной точки, и убедиться, что это действительно так.

б) А тут речь идёт о точках и векторах пространства. Сначала найдём векторы:   Надеюсь, эта простейшая задача у вас уже отработана.

По формуле   вычислим скалярное произведение:

К слову: скалярное произведение положительно, значит, угол между пространственными векторами   является острым.

Ответ: 

При некотором опыте скалярное произведение можно приноровиться считать устно.

Проверка векторов на ортогональность с помощью скалярного произведения

Вернёмся к важному случаю, когда векторы являются ортогональными. Напоминаю: векторы   и   ортогональны тогда и только тогда, когда  . В координатах данный факт запишется следующим образом:  (для векторов плоскости);  (для векторов пространства).

Пример 9

а) Проверить ортогональность векторов:   и   б) Выяснить, будут ли перпендикулярными отрезки   и  , если 

Решение:  а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: , следовательно, 

б) Здесь речь идёт об обычных отрезках плоскости (в чём сходство и различия вектора и отрезка, я очень подробно разъяснил на первом уроке). Речь идёт об обычных отрезках, а задача всё равно решается через векторы. Найдём векторы:

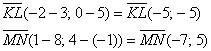
Вычислим их скалярное произведение: , значит, отрезки   и   не перпендикулярны.

Обратите внимание на два существенных момента:

– В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.

– В окончательном выводе «между строк» подразумевается: «если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными». Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках:  «значит,отрезки   и   не перпендикулярны».

Ответ: а)  , б) отрезки   не перпендикулярны.

Пример 10

Даны четыре точки пространства  . Выяснить будут ли перпендикулярными следующие прямые: а)  ; б)  .

Это задача для самостоятельного решения. В условии требуется проверить перпендикулярность прямых. А решается задача снова через векторы по полной аналогии с предыдущим примером. Геометрически тоже всё очевидно – если удастся доказать перпендикулярность векторов, то из этого автоматически будет следовать перпендикулярность соответствующих прямых. Четыре вектора, которые вы найдёте, называют направляющими векторами прямых.

Полное решение и ответ в конце урока.

Мощь аналитической геометрии – в векторах. Так, в рассмотренных примерах, с помощью скалярного произведения можно установить не только ортогональность векторов самих по себе, но и перпендикулярность отрезков, прямых. И это приоткрылась только малая часть красоты предмета.

Завершая разговор об ортогональности, разберу ещё одну небольшую задачу, которая время от времени встречается на практике:

Пример 11

При каком значении   векторы   будут ортогональны?

Решение: По условию требуется найти такое значение параметра  , чтобы данные векторы были ортогональны. Два вектора пространства   ортогональны тогда и только тогда, когда  .

Дело за малым, составим уравнение:

Раскрываем скобки и приводим подобные слагаемые:

Решаем простейшее линейное уравнение:

Ответ: при  В рассмотренной задаче легко выполнить проверку, в исходные векторы   подставляем полученное значение параметра  :

И находим скалярное произведение:  – да, действительно, при   векторы   ортогональны, что и требовалось проверить.

Пример 12

При каком значении   скалярное произведение векторов   будет равно –2?

Это простенький пример с векторами плоскости. Для самостоятельного решения.

Немного усложним задачу: