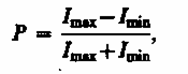Плоские и сферические электромагнитные волны. Монохроматичность и когерентность световой волны. Интерференция волн и света.

Плоской наз-ся волна, если ее поверхность имеет вид совокупно параллельных плоскостей,а сферической. Если совокупность сфер.

Когерентность волн – согласованная во времени и пространстве нескольких колебания волновых процессов.

Этому состоянию удовлетворяет монохромотичность волны – волны одной постоянной частоты.

Ни один реальный источник не дает строго монохромотичного света (исключ. – лазеры).

Предположим,2 монохроматич. световые волны накладываются друг на друга,возбуждая в определенной точке пространства колебания одного направления.

Уравнения 2-х волн:

х₁ = А₁cos(t +₁) и x₂ = A₂cos(t + ₂).

 Под х понимают напряженность электрического Е или магнитного Н полей волны; векторы Е и Н колеблются во взаимно перпендикулярных плоскостях

Амплитуда результирующего напряжения по теореме косинуса

A² = A²_l + A²₂ + 2A₁A₂ cos(₂ - ₁)

где = 1 - 2 = const.

Если волны когерентны, то cos (. ₁ – . ₂) = const должен быть постоянным. Но в каждой точке пространства различен

Тогда,

Интенсивн.результир. может быть, если :

cos(₂ - ₁) > 0, интенсивность I > I₁ + I₂ ,

где cos(₂ - ₁) < О, интенсивность I < I₁ + I₂. 

При наложении двух когерентных световых волны происходит пространственное перераспределение свеового поока, в результате в одном месте возникает max. В другом min. Это явление наз-ся интерференция света

Для некогерентных волн разность (₂ - ₁) непрерывно изменяется, поэтому среднее во времени значение cos(₂ - ₁) равно нулю, и интенсивность результирующей волны всюду одинакова и при  I₁ = I₂ равна 2I₁ (для когерентных волн при данном условии в максимумах I = 4I₁ в минимумах I = 0).

Для получ. Когерентных световых волн применяют метод разделения волны, излучая одним источником на 3 части. Которые при прохождении различных отпических путей накладываются друг на друга и дают интерф. картину Пусть волны раздел. На 2 когерентные, производная в точке О, а а в очке М наблюдается интерференц. Картина.

Одна волна прошла путь S₁ , вторая S₂, с показ. п_2.

первая волна в точке п возбужд. Колеб., ур-ние которых :

 А₁cos(t – s₁/v₁)

вторая волна возбуждает колебания. Уравнение которых

А₂cos(t – s₂/v₂),

 где v₁ = c/n₁, v₂ = c/n₂ - соответственно фазовая скорость первой и второй волны.

Разность фаз колебаний, возбуждаемых волнами в точке М, равна

  учли, что /с = 2v/с = 2₀ 

где ₀ - длина волны в вакууме

Произведение геометрической длины s пути световой волны в данной среде на показатель n преломления этой среды называется оптической длиной пути L, 

a  = L₂ – L₁ - разность оптических длин проходимых волнами путей - называется оптической разностью хода.

Если оптическая разность хода равна целому числу длин волн в вакууме

     то  = ±2m, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Следовательно, является условием интерференционного  максимума.

Если оптическая разность хода

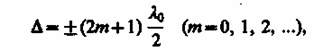            то  = ±(2m + 1), и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. условием интерференционного минимума.

Интеpфеpенция света. Интерференционное поле от двух точечных источников. Опыт Юнга.

Интерференция света- явление при котором происходит наложение двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности.

До лазеров когерентные волны получ. Раздел. И послед сведением световых лучей.исходящих отодного источника. С помощью щелей, зеркал, преломляющихся тел, щелей.

Метод Юнга. Источником света служит ярко освещенная щель S (рис. 245), от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂, параллельные щели S. Таким образом, щели S₁ и S₂ играют роль когерентных источников.

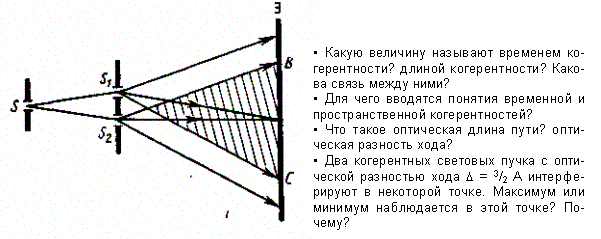
Расчет интерференционной картины от двух источников. Расчет интерференционной картины для рассмотренных выше методов наблюдения интерференции света можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу (рис. 248).

Щели S₁ и S₂ находятся на расстоянии d друг от друга и являются когерентными (реальными или мнимыми изображениями источника S в какой-то оптической системе) источниками света.

Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l≫d.

Начало отсчета выбрано в точке О, симметричной относительно щелей.

Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода  = s₂ – s₁ (см. § 172). Из рис. 248 имеем

         

 откуда s²₂ -  s²₁ = 2xd, или

 

 Из условия  l≫d следует, что s₁ + s₂  2l, поэтому

                                                   (173.1)

Подставив найденное значение  (173.1) в условия (172.2) и (172.3), получим, что максимумы интенсивности будут наблюдаться в случае, если

                (173.2)

 а минимумы -- в случае, если

                    (173.3)

 Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно

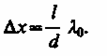                                   (173.4)

х не зависит от порядка интерференции (величины m) 

при большом расстоянии между источниками, например при d  l, отдельные полосы становятся неразличимыми.

Для видимого света ₀  10^-7 м,

поэтому четкая, доступная для визуального наблюдения интерференционная картина имеет место при l≫d 

Вpеменная и пpостpанственная когеpентность, pадиус когеpентности. Интерференция в тонких пленках.

Излучение атома происходит очень короткое время, порядка 10 ^-8 с. Атом после этого в норм. Состояние

При повторном возбуждении волна имеет новую начальную фазу ,т.е. излучение света атома минимально-прерывистое, в виде прерывистых называемых волновым цугом.

Время когерентн.

Расстояние

Расстояние при прохождении которого волны утрачивают когерентность , при …

- получ.интерф.картина

Когерентные колебания,которые совершаются в одной и той же точке пространства,с одределенной степенью монохром.волны наз-ся временем когерентн.

2 Источника размеры и взаиморасположение позволяет наблюдать интерференцию наз-ся пространственной когерентностью

Радиус когерен. Max поперечны направлению распостранения волны расстояние на котором возможно наблюдать интерференцию.

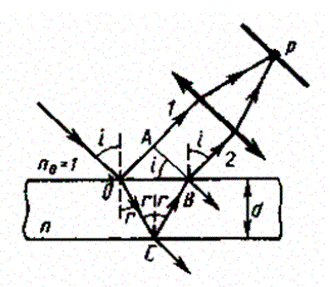
Пусть на плоскопараллельную прозрачную пленку с показателем преломления n и толщиной d под углом i (рис. 249) падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке О луч разделится на два: частично отразится от верхней поверхности пленки, а частично преломится. Преломленный луч, дойдя до точки С, частично преломится в воздух (n₀ = 1), а частично отразится и пойдет к точке В. Здесь он опять частично отразится (этот ход луча в дальнейшем из-за малой интенсивности не рассматриваем) и преломится, выходя в воздух под углом i. Вышедшие из пленки лучи 1 и 2 когерентны, если оптическая разность их хода мала по сравнению с длиной когерентности падающей волны. Если на их пути поставить собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы. В результате возникает интерференционная картина, которая определяется оптической разностью хода между интерферирующими лучами.

                    

показатель преломления окружающей пленку среды принят равным 1,

а член ±₀/2 обусловлен потерей полуволны при отражении света от границы раздела. Если n > n₀, то потеря полуволны произойдет в точке О и вышеупомянутый член будет иметь знак минус;

если же n < n₀, то потеря полуволны произойдет в точке С и ₀/2  будет иметь знак плюс. Согласно рис., ОС= СВ= d/cos г, ОА = OBsin I = 2d tgr sini.

 Учитывая для данного случая закон преломления sini = nsin r, получим

 

 С учетом потери полуволны для оптической разности хода получим

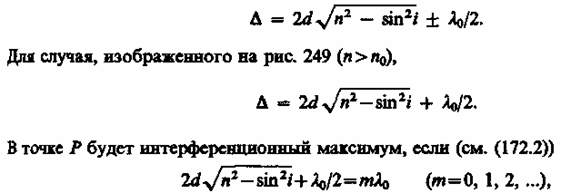
Применение интерференции света. Просветление оптики. Многолучевая интерференция. Интерферометр Майкельсона.

Явление интерференции обусловлено волновой природой света; его количественные закономерности зависят от длины волны До- Поэтому это явление применяется для подтверждения волновой природы света и для измерения длин волн (интерференционная спектроскопии).

Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий. Прохождение света через каждую преломляющую поверхность линзы, например через границу стекло - воздух, сопровождается отражением 4% падающего потока (при показа теле преломления стекла 1,5). Так как современные объективы содержат большое количество линз, то число отражений в них велико, а поэтому велики и потери светового потока. Таким образом, интенсивность прошедшего света ослабляется и светосила оптического прибора уменьшается. Кроме того, отражения от поверхностей линз приводят к возникновению бликов, что часто (например, в военной технике) демаскирует положение прибора.

Для устранения указанных недостатков осуществляют так называемое просветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления, меньшим, чем у материала линзы. При отражении света от границ раздела воздух - пленка и пленка - стекло возникает интерференция когерентных лучей 1 и 2'Просветляющий слой

Толщину пленки d и показатели преломления стекла n_с и пленки n можно подобрать так, чтобы волны, отраженные от обеих поверхностей пленки, гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность хода равна   - (см. (172.3)). Расчет показывает, что амплитуды отраженных лучей равны, если

 Так как n_с, n и показатель преломления воздуха n₀ удовлетворяют условиям n_с > n > n₀,  то потеря полуволны происходит на обеих поверхностях; следовательно, условие минимума (предполагаем, что свет падает нормально, т. е. I = 0)

где nd - оптическая толщина пленки. Обычно принимают m = 0, тогда 

 Таким образом, если выполняется условие (175.1) и оптическая толщина пленки равна ₀/4, то в результате интерференции наблюдается гашение отраженных лучей. Так как добиться одновременного гашения для всех длин волн невозможно, то это обычно делается для наиболее восприимчивой глазом длины волны ₀  0,55 мкм. Поэтому объективы с просветленной оптикой имеют синевато-красный оттенок.

Создание высокоотражающих покрытий стало возможным лишь на основе многолучевой интерференции. В отличие от двухлучевой интерференции, которую мы рассматривали до сих пор, многолучевая интерференция возникает при наложении большого числа когерентных световых пучков. Распределение интенсивности в интерференционной картине существенно различается; интерференционные максимумы значительно уже и ярче, чем при наложении двух когерентных световых пучков. Так, результирующая амплитуда световых колебаний одинаковой амплитуды в максимумах интенсивности, где сложение происходит в одинаковой фазе, в N раз больше, а интенсивность в N² раз больше, чем от одного пучка (N - число интерферирующих пучков). Отметим, что для нахождения результирующей амплитуды удобно пользоваться графическим методом, используя метод вращающегося вектора амплитуды (см. § 140). Многолучевая интерференция осуществляется в дифракционной решетке (см. § 180).

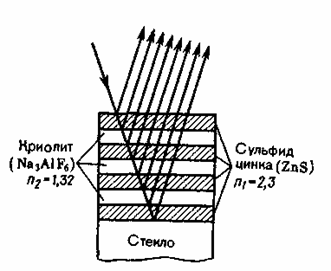
Многолучевую интерференцию можно осуществить в многослойной системе чередующихся пленок с разными показателями преломления (но одинаковой оптической толщиной, равной ₀/4), нанесенных на отражающую поверхность (рис. 254). Можно показать, что на границе раздела пленок (между двумя слоями ZnS с большим показателем преломления n₁ находится пленка криолита с меньшим показателем преломления n₂) возникает большое число отраженных интерферирующих лучей, которые при оптической толщине пленок ₀/4 будут взаимно усиливаться, т. е. коэффициент отражения возрастает. Характерной особенностью такой высокоотражательной системы является то, что она действует в очень узкой спектральной области, причем чем больше коэффициент отражения, тем уже эта область. Например, система из семи пленок для области 0,5 мкм дает коэффициент отражения   96% (при коэффициенте пропускания  3,5% и коэффициенте поглощения <0,5%). Подобные отражатели применяются в лазерной технике, а также используются для создания интерференционных светофильтров (узкополосных оптических фильтров).

 

                         

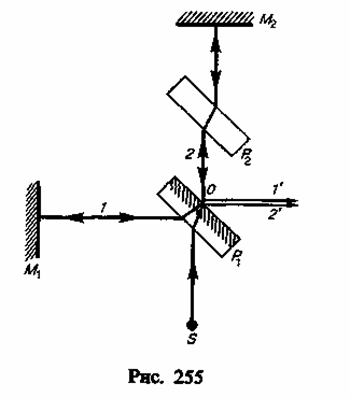
Явление интерференции также применяется в очень точных измерительных приборах, называемых интерферометрами. Все интерферометры основаны на одном и том же принципе и различаются лишь конструкционно. На рис. 255 представлена упрощенная схема интерферометра Майкельсона.

                          

. Дифракция волн и света. Принцип Гюйгенса-Френеля. Метод зон Френеля.

Дифракция – огибание волнами краев препятствий.

Наблюдается. Если размеры препятствий с волнами длины . объяснение этому принцип Гюгенса :

Каждая точка до которой доходит волна явл-ся источником вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.

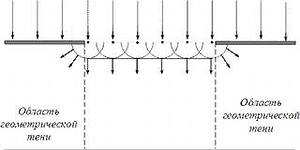
Принцип гюгенца не объяснял прямолинейность распостранения света.данный принцип дополнил Френель:

Вторичные волны интерферируют.

Объяснение данному принципу дет метод. зон Френеля

Источник S замен. Действ. Воображ.источн.. разлож. На волновой поверн. S /. S/ рабивается на кольцевые зоны.

Расстояние от границ зоны до т.О отлична λ/2, окончат. Результат т.О сложен.колеб. возник. От всех зон, т.е. колеб. От соседн.зон в т.О. приходят к противофазе

A = A1 – A2 + A3 – A4 + ..., где

A₁ , A₂- амплитутда колеб, возбужд. 1-ый, 2-ой

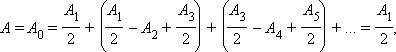
Т.к амплитуда соседних зон по величине близки. То выраж. В скобках в ур-ии 2 будет приблизительно равно 0. И тогда А _рез= А₁/2 т.е. действ. Всей открыт.волной поверхн.равно половине действ.ценрт.зоне Френеля.

Вывод: свет от любой точки фронта …. Идет во все стороны, но в слдествв. Интерфер. В т.О свет идет как бы внутри узкого канала диаметр , которого меньше радиуса первой зоны Френеля. Т.е. свет в т.О распостр.прямолинейно.

Сувелич.угл … действ. Зон френеля в т.О уменьш.

Правомерность деления волнового фронта на зоны Френеля потвержд.зонные пластинки – стеклянные пластины, сост.из .пластин черед из из прозрачных и не прозрачных концетр. Сфер, построенных по принципу расположения зон Френеля.

Если поместить такую пластинку между источником и экраном, то пластинка закроет все черные зоны Френяля, оставив не четные, при этом интенсивность т.О будет больше , чем без пластинки

A = A1 + A3 +A5 +…

Дифракция Френеля на простейших преградах: круглом отверстии и диске

Дифракция на круглом отверстии

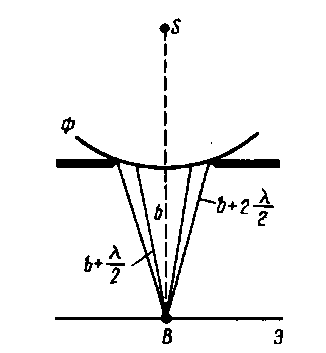
Разобъем волновой фронт S на зоны Ф. в т.В …

Если м четная , то А _рез и У =0

Если отверстие открывает одну зону Ф., то в Т. А _рез =А ₁, т.е. в 2 раза больше, чем в отсутствии экрана с отверстием, а интенсивность в 4 раза больше.

Дифракционная картина в Т.В будет иметь вид чередующихся темных и светлых колец с центром в т.В. причем, если м –четная – в центре темное кольцо, м-нечетное –светлое

(Сферическая волна, распространяющаяся из точечного источника  , встречает на своем пути экран с круглым отверстием. Дифракционная картина наблюдается на экране   в точке  . Разобьем часть волновой поверхности   на зоны Френеля. Вид дифракционной картины будет зависеть от количества зон Френеля, укладывающихся в отверстии. Амплитуда результирующего колебания в точке   равна:  (плюс для нечетных  , минус – для четных). Дифракционная картина от круглого отверстия вблизи точки   будет иметь вид чередующихся светлых и темных колец.)

Дифракция на диске

Сферическая волна, распространяющаяся из точечного источника  , встречает на своем пути диск. Дифракционная картина наблюдается на экране   в точке  . Пусть диск закрывает   первых зон Френеля. Тогда амплитуда результирующего колебания в точке   равна:  .  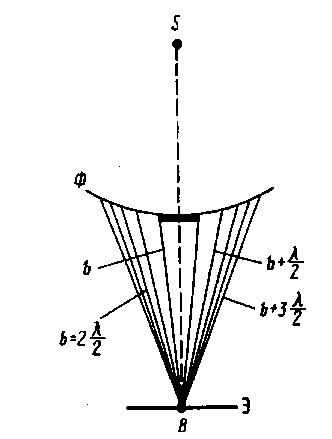Т.к. слагаемое в скобках равно 0, то  . Следовательно, в точке   всегда будет светлое пятно, окруженное концентрическими светлыми и темными кольцами, а интенсивность убывает с расстоянием от центров картины.

С увеелич. Радиуса диска интенсивн. Радиусча мах увел.

При больших размерах диска за ним тень и слабая картина

Дифракция Фраунгофера на одной щели

Плоская имуннохроматич.волна (волна одной частоты), падает нормально на щель MN, а-ширина(толщина) щели. Направлние лучей за щель может быть под разными углами ….

Рассмотр.лучи, которые отклон. На … от своего первоначального значения.

MF – разность хода крайних лучей.… F- основание перпендикуляра, опущенного из точки М на луч ND

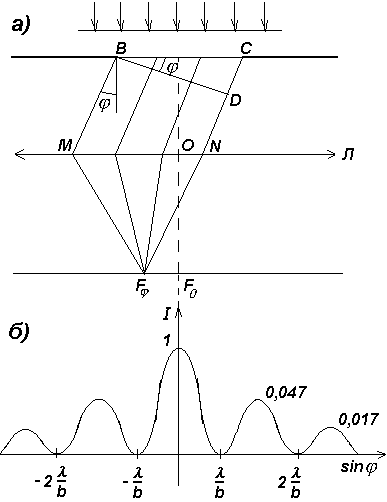
Щель разбиваем на зоны Ф.

Колебания от каждой пары соседних зон взаимогасят друг друга

Тогда в т.В.

если число зон Френеля четное, то

                    (179.2)

 и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то

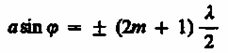                                (179.3)

и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля.

В направлении ….=0 наблюдается самый интенсивный центральный максимум нулевого порядка

Если ……., то дифракция не наблюдается., если на щель падает белый свет, то в центре наблд. – белая полоса (……..),а слева и справа – спектры –повторяющиеся

Дифракционная решетка как спектральный прибор. Разpешающая способность дифракционной pешетки

Диф.решетка- система парал.щели. равной ширины,лежащих в одной плоскости раздел.равными по ширине не прозрачными решетками

Рассмотрим дифракционную решетку. На рис. 262 для наглядности показаны только две соседние щели MN и CD. Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d = a + b называется постоянной (периодом) дифракционной решетки.

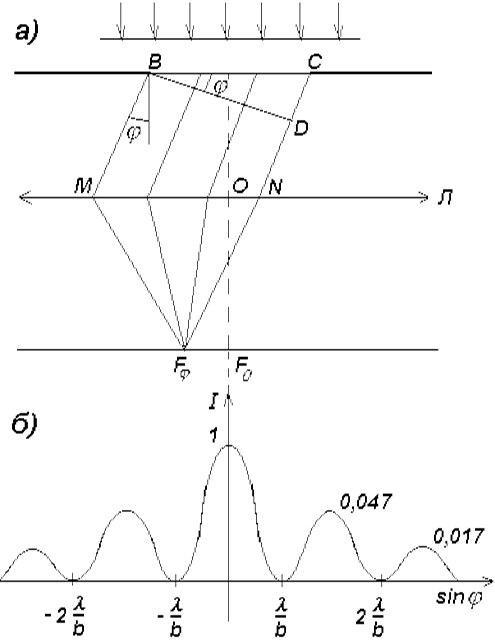
Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления j одинаковы в пределах всей дифракционной решетки:

Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т. е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (179.2):

                                    (180.2)

Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т. е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей /2, З /2, …,          посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (180.1) условие дополнительных минимумов:

 

 Наоборот, действие одной щели будет усиливать действие другой, если

                      (180.3)

 т. е. выражение (180.3) задает условие главных максимумов.

Таким образом, полная дифракционная картина для двух щелей определяется из условий:

 

число главных максимумов

т. е. определяется отношением периода решетки к длине волны.

Разрешающая способность дифракционной решетки. Пусть максимум m-го порядка для длины волны ₂ наблюдается под углом , т. e., согласно (180.3), dsin = m₂.

При переходе от максимума к соседнему минимуму разность хода меняется на /N (см. (180.4)), где N - число щелей решетки. Следовательно, минимум ₁ наблюдаемый под углом _min,удовлетворяет условию dsin_min = m₁ +₁/N. По критерию Рэлея,  = _min, т.е. m₂ = m₁ +₁/N или ₂/(₂ - ₁) = mN. Так как ₁ и  ₂ близки между собой, т. е.  ₂ - ₁ = , то, согласно (183.3),

Таким образом, разрешающая способность дифракционной решетки пропорциональна порядку m спектра и числу N щелей, т. е. при заданном числе щелей увеличивается при переходе к большим значениям порядка m интерференции. Современные дифракционные решетки обладают довольно высокой разрешающей способностью 

 Дифpакция pентгеновских лучей. Рентгеностpуктуpный анализ. Методы Лауэ и Дебая. Формула Вольфа - Брэггов.

Для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка, что и длина волны падающего излучения 

Кристаллы, являясь трехмерными пространственными решетками (см. § 181), имеют постоянную порядка 10^-10 м и, следовательно, непригодны для наблюдения дифракции в видимом свете (  510^-7 м). 

Эти факты позволили немецкому физику М. Лауэ (1879-1960) прийти к выводу, что в качестве естественных дифракционных решеток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с  рентгеновского излучения ( 10^-12   10^-8 м).

Метод рассчета диф.ренген.излуч. на крист. Решетки

Формула Вульфа-Брегга :

2dsin =m , m=1,2,3- 

где m - порядок дифракционного максимума.

Дифракц.ренген.излуч.явл-ся резутат. Его отраж. От сис-мы паралельны кристолографич.плоскостей (плоскостей, в которых лежеат атомы кристал.решетки)

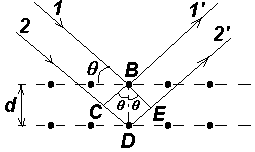
Представим кристаллы в виде совокупности параллельных кристаллографических плоскостей (рис. 264), отстоящих друг от друга на расстоянии d.

Пучок параллельных монохроматических рентгеновских лучей (1, 2) падает под углом скольжения  (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1 и 2', интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа - Брэггов

                                (182.1)

т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн А, наблюдается дифракционный максимум.

(При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться непрерывным рентгеновским спектром, испускаемым рентгеновской трубкой. Тогда дня таких условий опыта всегда найдутся длины волн А, удовлетворяющие условию)

Понятие о голографическом методе получения и восстановления изображений

Голография (от греч. «полная запись») - особый способ записи и последующего восстановления волнового поля, основанный на регистрации интерференционной кар тины. Она обязана своим возникновением законам волновой оптики - законам интерференции и дифракции.

Этот принципиально новый способ фиксирования и воспроизведения пространственного изображения предметов изобретен английским физиком Д. Табором (1900-1979) в 1947 г. (Нобелевская премия 1971 г.). Экспериментальное воплощение и дальнейшая разработка этого способа (Ю. Н. Денисюком в 1962 г. и американскими физиками Э. Лейтом и Ю. Упатниексом в 1963 г.) стали возможными после появления в 1960 г. источников света высокой степени когерентности - лазеров (см. § 233).

Рассмотрим элементарные основы принципа голографии, т. е. регистрации и восстановления информации о предмете. Для регистрации и восстановления волны необходимо уметь регистрировать и восстанавливать амплитуду и фазу идущей от предмета волны. В самом деле, согласно формуле (144.2), учитывая, что I ~ А², распределение интенсивности в интерференционной картине определяется как амплитудой интерферирующих волн, так и разностью их фаз. Поэтому для регистрации как фазовой, так и амплитудной информации кроме волны, идущей от предмета (так называемой предметной волны), используют еще когерентную с ней волну, идущую от источника света (так называемую опорную волну). Идея голографирования состоит в том, что фотографируется распределение интенсивности в интерференционной картине, возникающей при суперпозиции волнового поля объекта и когерентной ему опорной волны известной фазы. Последующая дифракция света на зарегистрированном распределении почернений в фотослое восстанавливает волновое поле объекта и допускает изучение этого поля при отсутствии объекта.

Практически эта идея может быть осуществлена с помощью принципиальной схемы, показанной на рис. 267, а. Лазерный пучок делится на две части, причем одна его часть отражается зеркалом на фотопластинку (опорная волна), а вторая попадает на фотопластинку, отразившись от предмета (предметная волна). Опорная и предметная волны, являясь когерентными и накладываясь друг на друга, образуют на фотопластинке интерференционную картину. После проявления фотопластинки и получается голограмма - зарегистрированная на фотопластинке интерференционная картина, образованная при сложении опорной и предметной волн.

 Для восстановления изображения (рис. 267, 6) голограмма помещается в то же самое положение, где она находилась до регистрации. Ее освещают опорным пучком того же лазера (вторая часть лазерного пучка перекрывается диафрагмой). В результате дифракции света на интерференционной структуре голограммы восстанавливается копия предметной волны, образующая объемное (со всеми присущими предмету свойствами) мнимое изображение предмета, расположенное в том месте, где предмет находился при голографировании. Оно кажется настолько реальным, что его хочется потрогать. Кроме того, восстанавливается еще действительное изображение предмета, имеющее рельеф, обратный рельефу предмета, т. е. выпуклые места заменены вогну ыми, и наоборот (если наблюдение ведется справа от голограммы).

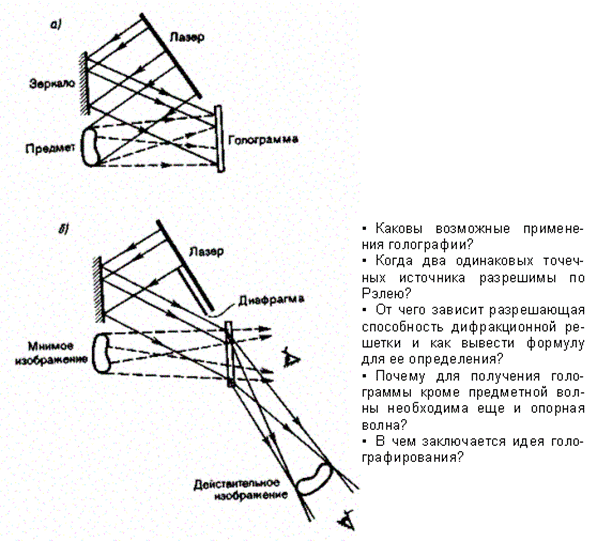
Рис. 267

Обычно пользуются мнимым топографическим изображением, которое по зритель ному восприятию создает полную иллюзию существования реального предмета. Рассматривая из разных положений объемное изображение предмета, даваемое голограммой, можно увидеть более удаленные предметы, закрытые более близкими из них (заглянуть за ближние предметы). Это объясняется тем, что, перемещая голову в сторону, мы воспринимаем изображение, восстановленное от периферической части голограммы, на которую при экспонировании падали также и лучи, отраженные от скрытых предметов. Голограмму можно расколоть на несколько кусков. Но даже малая часть голограммы восстанавливает полное изображение. Однако уменьшение размеров голо граммы приводит к ухудшению четкости получаемого изображения. Это объясняется тем, что голограмма для опорного пучка служит дифракционной решеткой, а при уменьшении числа штрихов дифракционной решетки (при уменьшении размеров голограммы) ее разрешающая способность уменьшается.

Методы голографии (запись голограммы в трехмерных средах, цветное и панорамное голографирование и т. д.) находят все большее развитие. Применения голографии разнообразны, во наиболее важными, приобретающими все большее значение, являются запись и хранение информации. Методы голографии позволяют записывать в сотни раз больше страниц печатного текста, чем методы обычной микрофотографии. По подсчетам, на фотопластинку размером 3232 мм можно записать 1024 голограммы (площадь каждой из них 1 мм²), т. е. на одной фотопластинке можно «разместить» книгу объемом свыше тысячи страниц. В качестве будущих разработок могут служить ЭВМ с топографической памятью, голографический электронный микроскоп, голографические кино и телевидение, топографическая интерферометрия и т. д.

 Поляризация света. Естественный и поляризованный свет. Форма и степень поляризации монохроматических волн. Закон Малюса

Естественный свет- Свет со всевозможными равновероятными ориентациями вектора Е (и, следовательно, Н) (а)

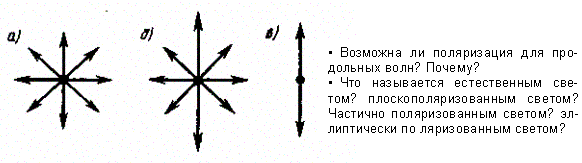
Поляризованный - Свет, в котором направления колебаний светового вектора каким-то образом упорядочены (б)

Частично поляризованный свет- если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление колебаний вектора Е

Плоскополяризованный (линейно поляризованный)- Свет, в котором вектор Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу(в)

Степенью поляризации называется величина