6. Расчет вероятности по функции нормального распределения.
В Excel для вычисления значений нормального распределения используются функция НОРМРАСП, которая вычисляет значения вероятности нормальной функции распределения для указанного среднего и стандартного отклонения. Функция имеет параметры: НОРМРАСП (х; среднее; стандартное_откл; интегральная), где: х — значения выборки, для которых строится распределение; среднее — среднее арифметическое выборки; стандартное_откл — стандартное отклонение распределения; интегральный — логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности распределения. Если 0, то будет плотность вероятности, если 1 – вероятность.
Для построения диаграммы нужно выделить полученные значения плотностей вероятностей и значения выборки.
7. Закон распределения выборочных средних. Стандартная ошибка средней.
Параметры совокупности выборочных средних. Средние величины для выборок (выборочные средние), сделанных из одной совокупности, могут рассматриваться как новая совокупность, которая характеризуется собственным распределением значений. Стъюдент предположил, что выборочные средние распределяются по закону нормального распределения и их совокупность характеризуются, таким образом, двумя параметрами:
M (с верхн.чёрточкой) – Средняя выборочных средних SM – Стандартное отклонение выборочных средних
Свойства параметров распределения выборочных средних (распределения Стъюдента):
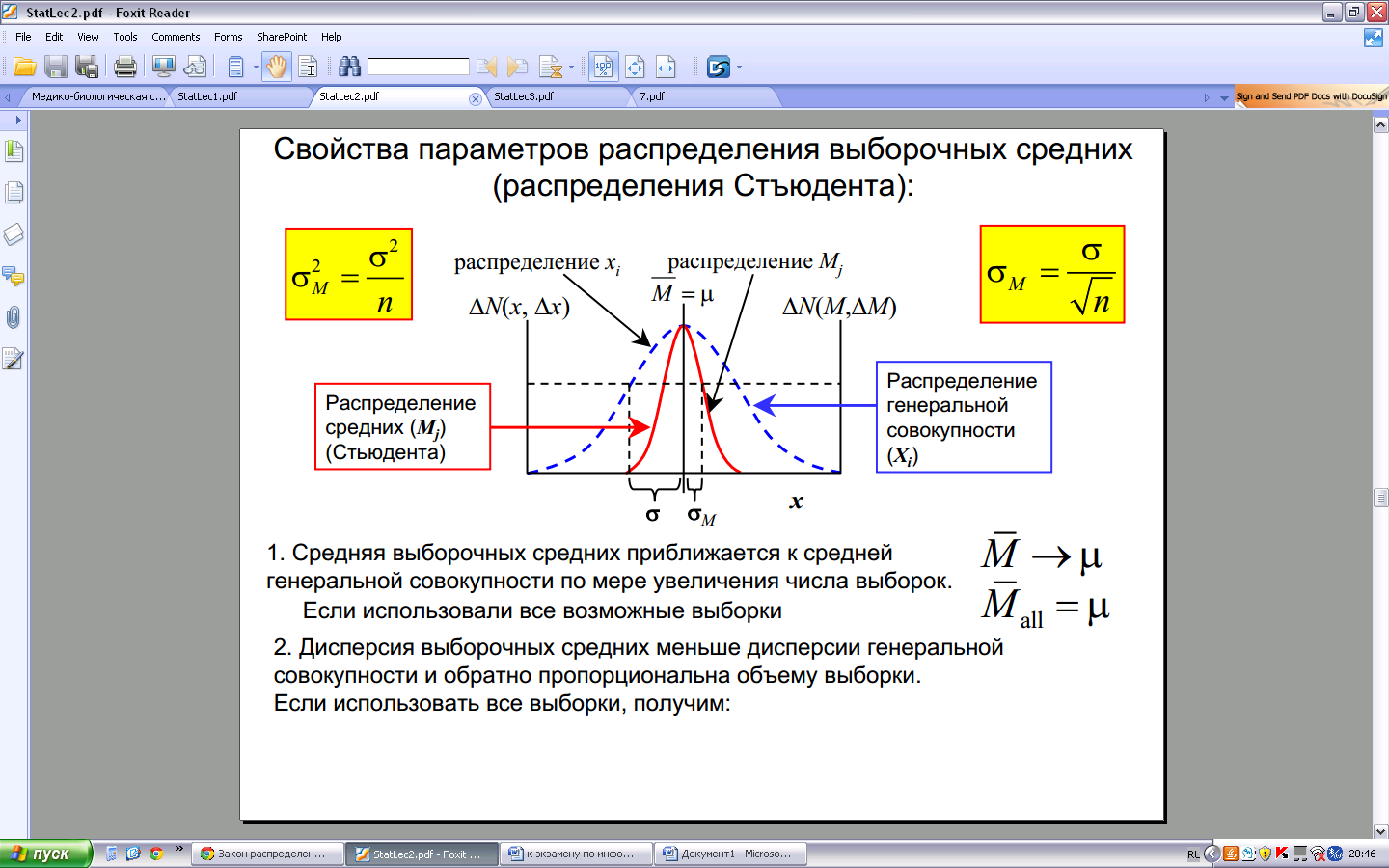
1. Средняя выборочных средних приближается к средней генеральной совокупности по мере увеличения числа выборок. 2. Дисперсия выборочных средних меньше дисперсии генеральной совокупности и обратно пропорциональна объему выборки.
Если использовать все выборки, получим: M(с чертой)→µ и M(с чертой)all =µ
К
ак
определить стандартную ошибку выборочной
средней по одной выборке? Эта величина
будет оценена с ошибкой
Это уравнение было получено Стъюдентом и Фишером. Оно справедливо только для выборок из нормального распределения!
Центральная предельная теорема 1.Выборочные средние имеют приближенно нормальное распределение независимо от распределения исходной совокупности, из которой были извлечены выборки. 2.Среднее значение всех возможных выборочных средних равно среднему исходной совокупности. 3.Стандартное отклонение всех возможных средних по выборкам данного объема, называемое стандартной ошибкой среднего, зависит как от стандартного отклонения совокупности, так и от объема выборки.
Соотношение между s.d. и SEМ
8. Алгоритм сравнения двух групп по одному параметру.
1) рассчитать t-критерий 2) число степеней свободы 3) воспользоваться таблицей
Находим М1 и М2, находим М1 – М2, по уравнению находим стандартные ошибки средних, находим сумму дисперсий средних, находим t.
9. t-критерий Стьюдента.
10. Расчет вероятности по t-критерию Стьюдента. Уровень значимости.
В биологии и медицине 0,05 или 0,01.
11. Функция Excel для вычисления распределения Стьюдента (синтаксис, аргументы).
Вероятност вычисляется так: Синтаксис: СТЬЮДРАСП(x;степени_свободы;хвосты) x — числовое значение, для которого требуется вычислить распределение (х – это будет t-критерий). Степени_свободы — целое, указывающее число степеней свободы. Хвосты — число возвращаемых хвостов распределения. Если хвосты = 1, функция СТЬЮДРАСП возвращает одностороннее распределение. Если хвосты = 2, функция СТЬЮДРАСП возвращает двустороннее распределение. Это от минус беск. До плюс беск или до плюс беск.. Обычно ставят 2.
t-критерий ищется через ABS (М1-М2)/сумм.ош.
12. Корреляция и ковариация (дать определения и математические формулы).
Корреля́ция (от лат. correlatio — соотношение, взаимосвязь), корреляционная зависимость — статистическая взаимосвязь двух или нескольких случайных величин. При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин.
Коэф.лин.корр-ии учитывает в большей степени дальние отклонения от среднего (удалённые точки). Это тоже не очень хорошо.
Ковариа́ция (взаимное отклонение) – мера линейной зависимости двух случайных величин.
ковариация это как дисперсия а корреляция это как отошение дисперсии к средней. то есть коррелл - относительный показатель.
ков=(сумма((xi-М)*(yi-М)))/n; r=ков/(стандотклон1*стандотклон2)
