5. Розрахувати акф по такій відомій спектральній щільності сигналу:

3 при 0    10

G()=

0 при   10

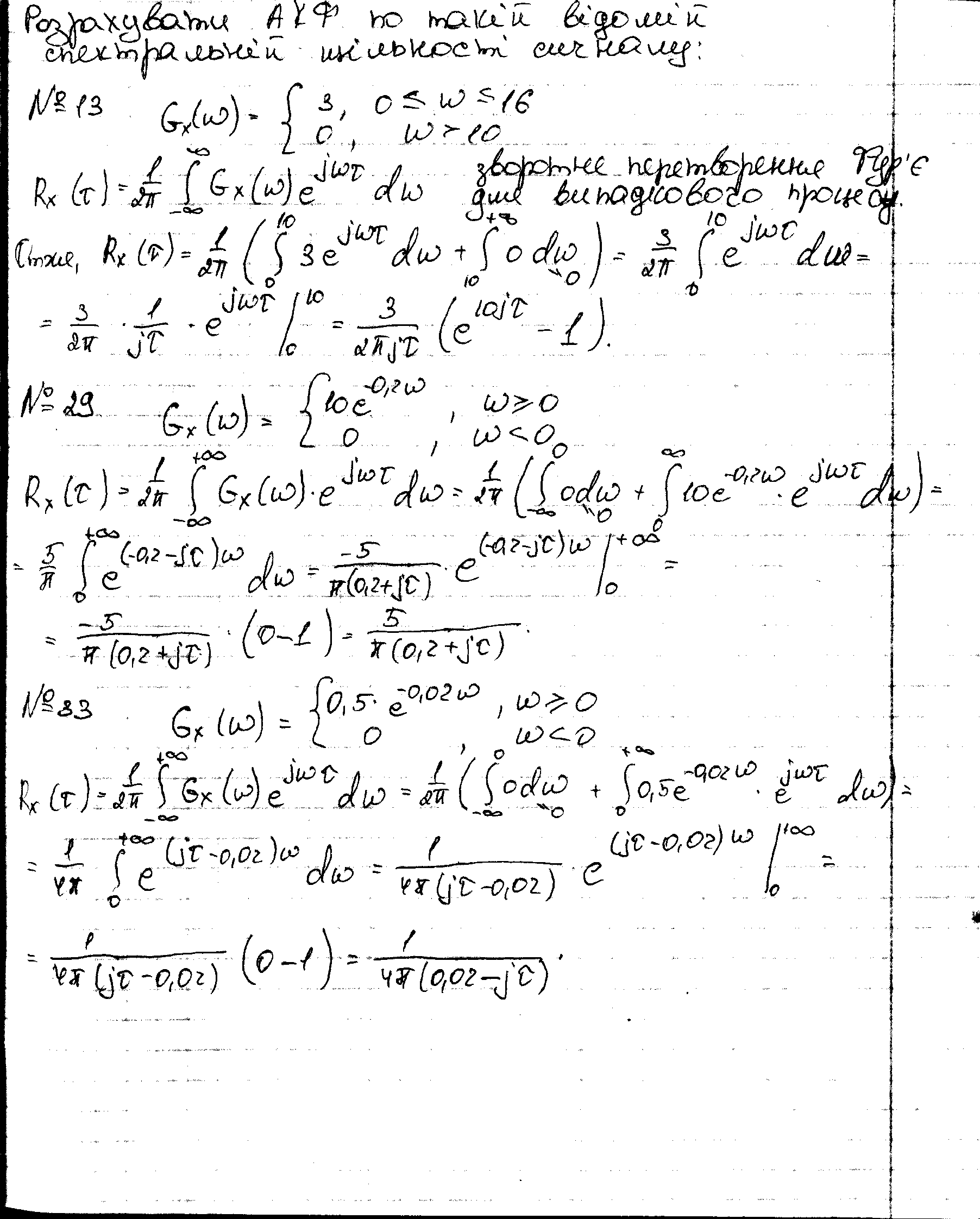
№14

1. Нормальний і нормалізований закони розподілу результатів спостережень і випадкових похибок.

Одним із найбільш широко розповсюджених законів розподілу є нормальний закон розподілу (закон розподілу Гауса), що пояснюється центральною граничною теоремою теорії ймовірностей. Центральна гранична теорема теорії ймовірностей стверджує, що розподіл випадкових величин (похибок) буде близьким до нормального кожний раз, коли результати спостережень формуються під впливом великої кількості незалежно діючих факторів, кожний із яких лише незначно впливає на результат в порівнянні із сумарною дією всіх інших факторів.

Диференціальна функція розподілу нормального закону розподілу випадкових величин описується:

де х, _х – відповідно середнє арифметичне і СКВ результатів спостережень.

Графічно ця функція показана на рис. 1 для різних

значень СКВ (_х1_х2):

Рисунок 1 .

На основі останнього рівняння можна встановити, що:

Щільність ймовірності має максимум при х=х=М[x].
Із збільшенням похибки незалежно від знаку (функція парна) щільність ймовірності наближається до нуля.
Із збільшенням СКВ _х ймовірність великих відхилень збільшується, тобто значення х розсіюються в більш широкому діапазоні.

Незважаючи на широке застосування нормального розподілу, він є лише моделлю реальних розподілів. Тому нормально розподілена випадкова величини, хоча і з малими ймовірностями, може приймати які завгодно великі значення.

Функція розподілу нормальної випадкової величини (інтегральна функція розподілу) має такий вид:

Якщо похибку виразити деяким безрозмірним параметром z середнього квадратичного відхилення, то отримаємо криву нормованого нормального закону розподілу (ННРЗ) з аргументом: , яка має наступний вираз: , .

Вираз для інтегральної функції нормованого нормального розподілу є таким:

За допомогою інтегральної функції ННРЗ Ф(z) можна визначити довірчу ймовірність попадання однократного спостереження х в задані границі :

Довірча ймовірність попадання однократного спостереження х в несиметричну відносно осі Оz зону запишеться: ,

де z_в і z_н – відповідно верхня і нижня

границі несиметричної зони; Ф(z_в) і Ф(z_н) – значення інтегральної функції для z=z_в і z=z_н.

Вказані вище граничні значення випадкової величини і наз. довірчими границями результату спостереження х з довірчою ймовірністю .

Так, для довірчих границь відхилень, які дорівнюють , тобто , довірча ймовірність буде такою: . Тобто . Звідси слідує, що результати спостереження з відхиленнями мають 68%-ну довірчу ймовірність.