5. Розрахувати спектральну щільність сигналу по такій відомій його акф:

5 + 10 при -2    0

R_x()= -5 + 10 при 0    2

0 при   -2; 2.

№13

1. Поняття інтегральної і диференційної функції розподілу результатів спостережень і випадкових похибок.

При вимірюванні деякої фізичної величини х кожний із результатів спостереження є випадковою величиною, яка може приймати різні значення х_і, де і – номер спостереження.

Результати спостереження деякої фізичної величини є випадковими величинами і можуть бути описані інтегральною і диференційною функціями розподілу.

Під інтегральною функцією розподілу результатів спостережень F(x) розуміють ймовірність того, що результат спостережень х_і в і-му досліді буде меншим деякого значення х, тобто

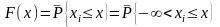, де Р – символ ймовірності події, вказаної у фігурних дужках.

На рис. 1,а значення інтегральної функції в точці х чисельно дорівнює ймовірності того, що випадкова величина х_і внаслідок і-го спостереження буде лівіше точки х. При переміщенні точки х вздовж осі ОХ ця ймовірність буде змінюватись і буде зростати. Тому інтегральна функція розподілу F(x) є зростаючою функцією аргумента х. Значення інтегральної функції розподілу в загальному випадку при переміщенні точки х від 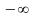до буде змінюватися від 0 до 1. теоретично інтегральна функція F(x) є неперервною, тобто результат спостереження може приймати будь-яке заздалегідь вибране значення в інтервалі від до з ймовірністю 1. Практично роздільна здатність ЗВ ділить всю область значень вимірюваної величини на відрізки, в межах яких спостерігач не відчуває зміни вимірюваної величини. Тому в межах кожного такого відрізка інтегральна функція зберігає постійні значення і стрибкоподібно змінюється при переході межі на деяку величину. В цифрових вимірювальних системах ці величини чітко відповідають одиниці останнього розряду, а в аналогових приладах – деякій долі поділки.

У більшості випадків приведені вище обставини не заперечують вважати інтегральну функцію розподілу результатів спостережень безперервною функцією, що спрощує аналіз випадкових похибок.

Початок координат для похибок  буде відповідати значенню х=Q.

Інтегральна функція розподілу похибок F_() відповідає інтегральній функції розподілу результатів спостереження х_і, тобто

.

В метрології для опису випадкових похибок вимірювань використовують диференційну функцію розподілу р(х), яка є похідною від інтегральної функції розподілу по аргументу х, тобто , .

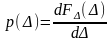Диференційну функцію розподілу р(х) частіше називають щільністю ймовірності, а графічне її зображення – кривою розподілу.

Інтегральна функція розподілу F(x) отримується інтегруванням диференційної функції розподілу р(х), тобто

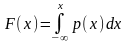
Щільність ймовірності р(х) задовольняє таким умовам: , .

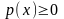Друга умова наз. умовою нормування щільності ймовірності, тобто площа під кривою розподілу в межах зміни х від до дорівнює 1 (ймовірність появи результату спостереження у вказаному інтервалі є вірогідною подією).

Добуток 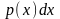називається елементом ймовірності і рівний тому, що випадкова величина х прийме значення в інтервалі .

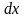Маючи криву розподілу р(х) можна визначити ймовірність попадання результату спостереження в любий заданий інтервал х:

.

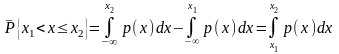Знаючи інтегральну функцію розподілу, ймовірність попадання результату спостереження х у вказаний інтервал визначають як різницю значень функції розподілу на границях цього інтервалу: .

По формі кривої розподілу р(х) можна судити про те, які інтервали значень випадкових похибок більш вірогідні, а які ні.

Координата, яка відповідає центру площі фігури, обмеженої кривою розподілу р(х) і віссю абсцис ОХ наз. математичним сподіванням М[х]:

.

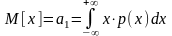Таким чином, матем. сподівання випадкової величини х є деяким постійним числом, яке в свою чергу є параметром розподілу. Числове значення вимірюваної величини, яке відповідає матем. сподіванню, приймають за істинне значення Q, тобто: Q=M[x].

Математичне сподівання похибки вимірювання – це деяка середня постійна похибка, яка повторюється в кожному і-му спостереженні. Ця похибка є систематичною похибкою.

Математичним сподіванням похибки вимірювання наз. деяка величина, на яку відрізняється оцінка істинного значення M[x] від істинного значення Q. Таким чином систематична похибка визначається як відхилення мат. сподівання результатів спостережень від істинного значення вимірюваної величини: ,

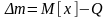а випадкова похибка – це різниця між результатом однократного спостереження і мат. сподіванням результатів: .

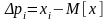Будь-яка похибка однократного спостереження може бути представлена як сума систематичної і випадкової похибок, тобто: .

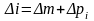Так як систематична похибка є постійною до деякої сукупності результатів спостережень, а випадкова похибка змінюється по величині і знаку для кожного однократного спостереження, істинне значення вимірюваної величини визначається:

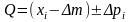
Значенн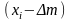я наз. виправленим результатом, якщо значення 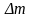вдається визначити на основі аналізу результатів експерименту. Коли в результаті однократного спостереження невідомі обидві складові похибки вимірювання, результат вимірювання може записаний:

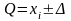,  - границя похибки вимірювання, яка рівна максимальному значенню суми і 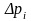по модулю.