3. Описание объекта

Приложение 3D графики создает модель, в котором объекты задаются как совокупность тел и поверхностей. Тела могут иметь разнообразную форму, описанную каким-либо математическим способом. Проще всего иметь дело с многогранниками, у которых каждая грань представляет собой часть плоскости, ограниченной полигоном. Описание такого тела относительно несложно - оно состоит из упорядоченного списка вершин. Сложнее дело обстоит с объектами, имеющими не плоские (криволинейные) поверхности. В этом случае в модели поверхности описываются сплайнами (кривыми, которые задаются сложными нелинейныеми уравнениями), однако для дальнейших построений их использование проблематично из-за требуемых громадных объемов вычислений. Для упрощения задачи криволинейные поверхности апроксимируются полигонами, и, конечно же, чем мельче полигоны, тем ближе апроксимация к модели, но и тем более громоздким становится описание объекта, а, следовательно, и больше времени требуется на его обработку. Представление криволинейной поверхности совокупностью плоских граней-полигонов называется тесселяцией (Tesselation). Слово "tessera", от которого произошел этот термин, означает кубики из смальты, из которых художники собирают мозаику. Как и смальтовые кубики, полигоны-грани должны быть простыми (не пересекающими себя), плоскими и выпуклыми - эти ограничения заметно упрощают их дальнейшую обработку.

Сплайны

Сплайн - гладкая кривая, которая проходит через две или более контрольных точек, управляющих формой сплайна. Два из наиболее общих типов сплайнов - кривые Безье (Bezier curves) и В-сплайны (B-spline curves). Типичным примером сплайнов являются также неоднородные рациональные B-сплайны (Non-Uniform Rational B-Spline - NURBS).

Сплайны состоят из вершин (vertices) и сегментов (segments). Каждая вершина сплайна имеет касательные векторы (tangents), снабженные на концах управляющими точками, или маркерами (handels). Маркеры касательных векторов управляют кривизной сегментов сплайна при входе в вершину, которой принадлежат касательные векторы, и выходе из нее.

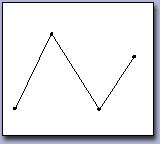
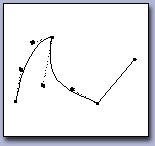
Кривая Безье - полиномиальная кривая, задаваемая набором определяющих точек. Представляет уравнение порядка на одну ступень меньше количества учитываемых точек.

B-сплайн - это любая гладкая кривая, определенная в трехмерном пространстве, нормаль которой может иметь любое направление (другими словами, она может искривляться в любом направлении)

NURBS. Неоднородный означает, что различные области объектов NURBS (кривых или поверхностей) обладают различными свойствами (весами), значения которых не равны между собой. Рациональный означает, что объект NURBS может быть описан с помощью математических формул. Большинство современных САПР и систем компьютерной анимации поддерживают моделирование с использованием NURBS. Моделирование на основе неоднородных рациональных B-сплайнов обладает следующими преимуществами перед другими методами:

• с помощью NURBS проще имитировать поверхности природных объектов или объектов, поверхности которых имеют сложным образом искривленные профили

• NURBS-модели обеспечивают лучшее качество визуализации закругленных краев объектов благодаря разбиению на грани, выполняемому с использованием аналитических выражений.

Лекция 11. ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ (4 часа)

План