1. Оптимальное решение. Критериальная функция.

Оптимальность – наилучший вариант ПР. Критерий – значимая, понятная ЛПР, хорошо им интерпретируемая характеристика исхода принятого решения.

Ситуацию мы измеряем при помощи критериев. F = зависимость от факторов = критериальная функция. Могут быть одно (монокритериальные, скалярные) и многокритериальные (критерии, которые должны быть достигнуты одновременно – поликритериальные или векторные).

2. Парная антагонистическая игра: формальное описание.

Парная игра разыгрывается между двумя игроками. Будем именовать их игрок 1 и игрок 2. Кроме того, условимся в дальнейшем, выступая в роли ЛПР, рассуждать и действовать на стороне игрока 1; при этом игрок 2 будет выступать в роли «противника».

Обозначим через X и Y множества возможных стратегий игрока 1 и игрока 2 соответственно. Величины x Є X и y Є Y будут обозначать конкретные стратегии игроков 1 и 2. Каждая конкретная стратегия игрока представляет собой некоторую совокупность указаний, определяющих последовательность его личных ходов в некоторой конкретной партии игры.

Игра может содержать, кроме личных ходов, и случайные ходы. Обозначим через H множество случайных стратегий. Любая конкретная стратегия hЄH представляет собой некоторую последовательность всех случайных ходов в некоторой конкретной партии игры. Каждая конкретная стратегия h будет происходить с некоторой вероятностью P(h), которая может быть подсчитана на основании вероятностей каждого случайного хода в этой последовательности; последние задаются правилами игры.

Функция P(h) представляет собой распределение вероятностей на пространстве H и должна удовлетворять условиям:

P(h) ≥ 0, (3.1)

Обозначим через g некоторый конкретный вариант игры, то есть некоторую индивидуальную партию игры. Каждая партия игры будет определена, если выбраны стратегии игроков 1 и 2, то есть xЄX и yЄY, и стратегия случайных ходов hЄH. Следовательно, всякая конкретная партия g игры определяется тремя элементами x, y, h.

Будем условно обозначать конкретную партию игры в виде

g = (x, y, h) (3.2)

Результатом партии игры является выигрыш (или проигрыш) каждого из игроков. Этот результат не всегда имеет количественное выражение. Однако для получения количественных оценок принимаемых решений результат игры необходимо хотя бы условно, представить числом (например, выигрыш – 1, проигрыш – 0, ничья – 0,5).

Рассмотрим одну из конкретных партий игры g = (x, y, h) и обозначим через L₁ (x, y, h) и L₂ (x, y, h) величины проигрыша первого и второго игрока соответственно. Условимся проигрышу приписывать знак «+», а выигрышу –

«-», то есть выигрыши рассматривать как отрицательные проигрыши. Общая сумма L_∑ (x, y, h) проигрышей обоих игроков в партии g = (x, y, h) равна

L_∑ (x, y, h) = L₁ (x, y, h) + L₂ (x, y, h) (3.3)

В парной антагонистической игре общая сумма проигрышей L_∑ (x, y, h) равна нулю: проигрыш одного игрока – выигрыш другого.

Проигрыш игрока 2 в теории игр называется потерями. С их помощью оценивают результат игры. Обозначим потери как L (x, y, h). Очевидно, что

L (x, y, h) = L₂ (x, y, h) = - L₁ (x, y, h) (3.4)

Поскольку стратегия h является случайной, то при выбранных стратегиях x и y игроков 1 и 2 потери L (x, y, h) будут случайной величиной с распределением вероятностей P(h) на множестве H случайных стратегий. Чтобы оценить выбранные стратегии x и y игроков на бесконечном множестве партий игры, прибегнем к приему усреднения потерь L (x, y, h) по всему множеству случайных стратегий H, для чего введем понятие средних потерь L_ср(x, y), определяемых по формуле для математического ожидания случайной величины:

L_ср (x, y) = (3.5)

Лиля, наверное, тут надо остановиться

Функция L_ср (x, y) в теории игр называется функцией средних потерь или просто функцией потерь. Очевидно, что при многократном повторении партий игры с одними и теми же конкретными стратегиями x и y игроков суммарный проигрыш игрока 2 (а значит и суммарный выигрыш игрока 1) стремится к величине функции средних потерь L_ср (x, y). В этом смысле последняя является характеристикой качества стратегий игроков (результат игры как бы «очищается» от влияния случайных стратегий h Є H).

В теории игр принято считать, что парная антагонистическая игра формально определена, если перечислены все возможные стратегии игроков 1 и 2, то есть заданы множества стратегий X и Y, и для любых конкретных стратегий x Є X и y Є Y определена функция потерь L_ср (x, y). Таким образом, мы приходим к следующему формальному определению игры:

Игра G определяется тремя элементами X, Y, L_ср, что условно можно записать в виде

G = (X, Y, L_ср) (3.6)

Игры, в которых каждый игрок имеет конечное число стратегий (конечные игры), удобно задавать с помощью так называемых матриц потерь. В случае игры с нулевой суммой достаточно задавать одну матрицу. Пусть G – некая конечная игра с нулевой суммой, в которой игрок 1 имеет m возможных стратегий, игрок 2 – n возможных стратегий, то есть X и Y есть конечные множества.

X = {x₁, x₂, … x_n},

Y = {y₁, y₂, … y_n}.

Тогда матрица порядка m*n

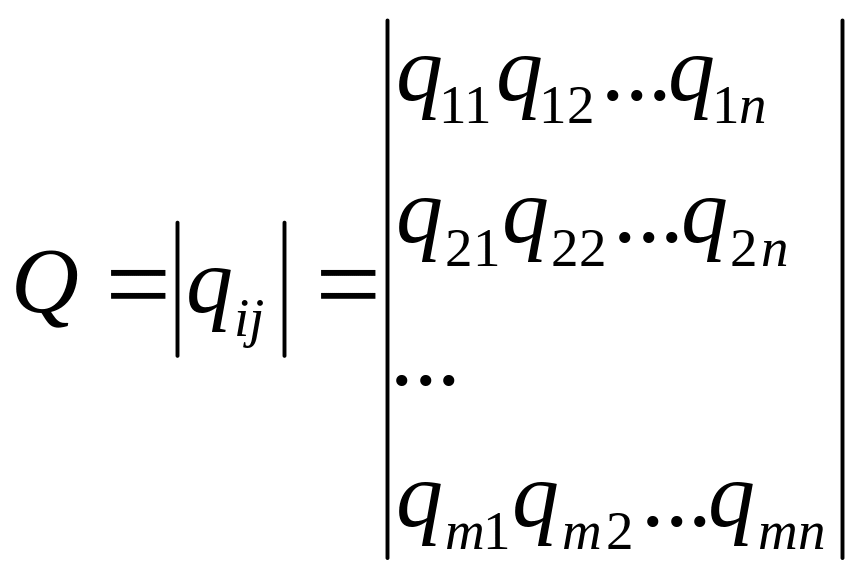, (3.7)

элемент которой q_ij = L_ср (x_i, y_i), называется матрицей потерь. Элемент матрицы q_ij, очевидно, имеет смысл средних потерь игрока 2 при реализации игроками стратегии x_i и y_i, иначе – среднего платежа игрока 2 игроку 1, если игрок 1 предпринимает стратегию x_i, а игрок 2 – стратегию y_i. Отсюда другое название матрицы потерь – платежная матрица.

С использованием платежной матрицы Q конечная парная антагонистическая игра G может быть формально определена тремя элементами X, Y, Q, что условно можно записать в виде:

G = (X, Y, Q) (3.8)

где

X = {x_i}, i Є 1,m – m-мерное множество возможных стратегий игрока 1;

Y = {y_i}, j Є 1,n – n-мерное множество возможных стратегий игрока 2;

Q = {q_ij}, i Є 1,m j Є 1,n – платежная матрица размера m*n.

Билет №12