2. Понятие игры с седловой точкой.

Существуют игры, для которых максимин (элемент платежной матрицы, равный максимуму из минимумов по строкам матрицы) равен минимаксу (элемент матрицы, который равен минимуму из максимумов по столбцам матрицы), то есть v₁ = v₂. Соответствующий элемент платежной матрицы называется седловой точкой. Иначе, седловой точкой называется элемент, который является одновременно минимальным в своей строке и максимальным в своем столбце.

	y1	y2	y3	qi min
x1	1	3	10	1
x2	6	4	5	4 maxmin
x3	8	3	2	2
qj max	8	4 minimax	10

Элемент платежной матрицы, соответствующий ее седловой точке (если она существует), называется чистой ценой игры. Обозначим ее через v. Совокупность минимаксных стратегий и чистая цена игры v являются решением игры с седловой точкой или, иначе, решением игры в чистых стратегиях (стратегия, выбираемая игроком в результате сознательного акта, без привлечения какого-либо случайного механизма).

В этих условиях если один из игроков узнает о намерении другого придерживаться минимаксной стратегии, то эта информация вынуждает его придерживаться своей минимаксной стратегии, а, значит, в игре с седловой точкой нет необходимости скрывать свои намерения.

Билет №20

1. Детерминированные зпр и зпр в условиях неопределенности.

1. Зависит от стратегии и фиксированных неконтролируемых факторов. В формуле в скобках (X, A). При заданных характеристиках фиксированных неслучайных неконтролируемых факторов A найти такую стратегию x штрих из множества стратегий X области определения омега, которая по возможности максимизировала или минимизировала бы критерий F.

2. Связано со множеством исходов.

a) просто в условиях неопределенности. В формуле в скобках (X, A, Z). При заданных характеристиках фиксированных неслучайных неконтролируемых факторов A, неопределенных факторов Z найти такую стратегию x штрих из множества стратегий X области определения омега, которая по возможности максимизировала или минимизировала бы критерий F.

b) в условиях неопределенности, вызванной факторами стохастической природы (игры с природой). В скобках (X, A, Y, Z).

2. Методы решения игр с седловой точкой.

Рассмотрим конечную игру G = (X, Y, Q) размера m*n, где множества стратегий X = {x_i}, Y = {y_i} и платежная матрица Q = |q_ij|, i Є 1,m, j Є 1,n заданы.

Поскольку в реальных ситуациях чистых стратегий не бывает, требуется найти решение игры в смешанных стратегиях (добавляется фактор вероятности), то есть цену игры v_p и две оптимальные смешанные стратегии P¹ = (p¹_i) и P² = (p²_i), где P¹ и P² – вероятностные векторы, компоненты которых удовлетворяют условиям:

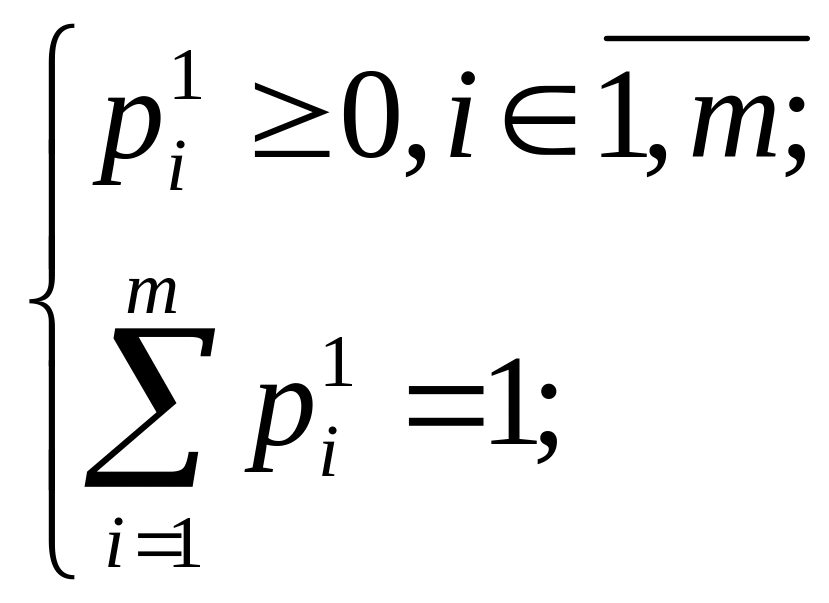(3.12)

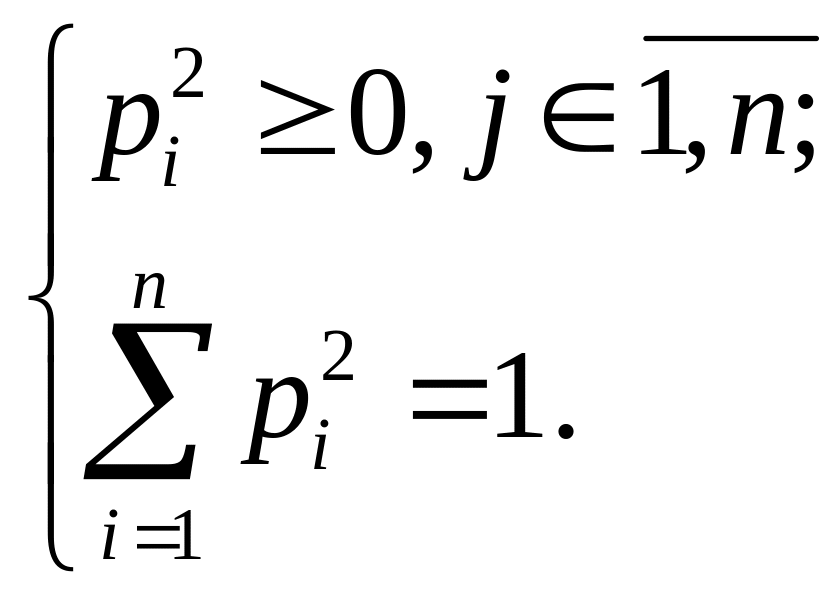(3.13)

Будем сначала искать оптимальную стратегию P¹ игрока 1. При ее определении будем исходить из свойств оптимальной стратегии, а именно будем учитывать, что эта стратегия должна обеспечить игроку 1 выигрыш не меньший v_p, при любом поведении противника, и равно v_p – при его оптимальном поведении.

Цена игры v_p пока неизвестна. Будем считать, что v_p > 0. Чтобы это условие выполнялось, достаточно, чтобы все элементы платежной матрицы Q = |q_ij| были неотрицательными, то есть q_ij ≥ 0. Этого всегда можно добиться, прибавляя ко всем элементам q_ij достаточно большое число M. При этом цена игры увеличится на М, а оптимальные стратегии не изменятся.

Предположим, что игрок 1 применяет свою смешанную стратегию P¹, а игрок 2 – чистую стратегию y_i. Тогда средний выигрыш игрока 1, обозначенный q¹_j, равен

q¹_j = = p¹₁q_1j + p¹₂q_2j + … + p¹_mq_mj, j Є 1,n (3.14)

Поскольку ищется оптимальная стратегия игрока 1, то его средний выигрыш q¹_j должен удовлетворять условию q¹_j ≥ v_p, откуда следует n условий:

(3.15)

Введем обозначения

L₁ = 1 / v_p;

z¹_i = p¹_i / v_p , i Є 1,m.

С использованием введенных обозначений из (3.12) и (3.15) получаем:

(3.16)

(3.17)

(3.18)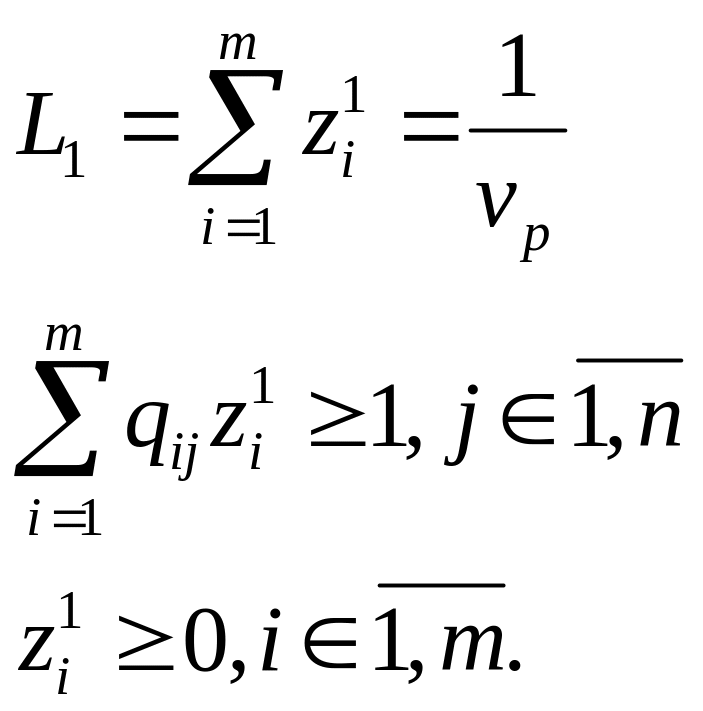

Поскольку игрок 1 стремится максимизировать свой выигрыш (доставить максимум цене игры v_p), то это равносильно требованию минимизировать величину L₁ = 1/v_p, то есть равносильно требованию

L₁ = (3.19)

Аналогичным образом можно найти оптимальную стратегию игрока 2.

Билет №21

1. Общая постановка однокритериальной статической детерминированной задачи принятия решения.

В скобках в формуле (X, A). При заданных характеристиках фиксированных, неконтролируемых, неслучайных факторов А найти такую стратегию из множества стратегий X области определения омега, которая по возможности обращала бы критерий F в минимум или максимум.

2. Принятие решений в условиях действия неопределенных факторов стохастической природы.

в тетради, где я показал

Билет №22

1. Методы решения однокритериальных статических детерминированных задач принятия решения.

на ксероксе

2. Максиминный критерий Вальда.

В соответствии с этим критерием, если требуется гарантия, чтобы выигрыш в любых условиях оказывался не меньше, чем наибольший из возможных в худших условиях (то есть линия поведения по принципу "рассчитывай на худшее"), то оптимальным решением будет то, для которого выигрыш окажется максимальным из всех минимальных при различных вариантах условий.

Критерием Вальда «рассчитывай на худшее» (критерий крайнего пессимизма) называют критерий, предписывающий обеспечить значение параметра эффекта равного α.Этот критерий ориентирует лицо, принимающее решение, на наихудшие условия и рекомендует выбрать ту стратегию, для которой выигрыш максимален. В других, более благоприятных условиях использование этого критерия приводит к потере эффективности системы или операции.

Билет №23