Два подхода к измерению информации: содержательный (субъективный) и алфавитный (объктивный).

содержательный (субъективный):

Зависит от субъекта. О от что он знает, а что не знает, что для него будет является информацией, а что нет. ЕХ: Париж столица Франции – не информация, Высота Эйфелевой башни … м.- информация., Или 2*2=4 и китайский язык.

Информация появляется только в процессе убыли энтропии. Можно пользоваться формулой:

I=H₁-H₂,

где I-информация, H₁- энтропия до опыта, H₂ – энтропия после опыта.

Если в результате опыта информация не изменилась, то информация была нулевой. Количество информации численно равно кол-ву вопросов с равновероятными бинарными вариантами ответов, которые необходимо задать, чтобы исключить неопределенность. I=H₁-H₂= log₂n - формула Хартли. (1бит = уменьшает неопределенность в 2 раза.)

алфавитный (объективный):

Содержание информация, а информация – это набор знаков, чем больше знаков, тем больше информации

Вопрос №4. Измерение информации в случае равновероятных событий. Формула Хартли.

Вероятность – величина, характеризующая вероятность происхождения действия.

Противоположная величина – неопределенность.

Мы будем следить за неопределенностью. Неопределенность случайного события будет зависеть от некоторого числа исходов события n.

F(n) – определяет неопределенность случайного события.

Все n вариантов равновероятны.

Свойства f(n):

1. f(1)=0, т.к. никакой неопределенности не будет.

2. Если n будет расти, то f(n) будет увеличиваться. n-> .

3. Пусть у нас имеется сложное событие (св-во. аддитивности): f(n₁;n₂) = f(n₁)+f(n₂). Общая неопределенность двух событий равна сумме неопределенностей этих событий.

4. При равновероятных событиях функция f будет max.

Какая функция удовлетворяет всем этим выше перечисленным условиям? Это логарифм. log_an.

f(n)= log_an

log_aв∙log_an – переход к новому основанию (!!!!log_aв=const!!!!).

а влияет на единицу измерения.

Очень удобно выбрать основание а=2.

Тогда f(n)= log₂n. Это нам удобно.

Рассмотрим случай, когда n=2: f(2)= log₂2=1.

Если событие имеет 2 равновероятных исхода, то вероятность происхождения события равна 1. Энтропия H-мера неопределенности.

H= log₂n - формула Хартли 1928 год. (2^H=n).

Эта формула предполагает равновероятность всех событий.

Преобразуем формулу Хартли к другому виду; он будет менее удобным, но более удобным для теоретического обобщения (для вывода следующей формулы)

Этим занимался Шеннон, он обобщил формулу ,он искусственно преобразовал её для рабочих целей.

P_i=1/n (P_i- вероятность).

Попробуем найти энтропию для отдельно взятого события. События равновероятные: H₁=H/n H- общая энтропия для всего события. H₁- доля, приходящаяся на одно событие (исход).

1/n log₂n P_i log₂1/ P_i Избавимся от дроби, используя cв-во. логарифмов: -P_i log₂P_i- это ответ. Разбили энтропию между всеми исходами.

Вопрос №5 Измерение информации в случае неравновероятных событий. Формула Шеннона. Формула Шеннона используется в тех случаях, когда вероятности исходов различны (в отличие от формулы Хартли)

Есть некое событие А, с разными исходами, n- число исходов события.

Ai	A1 A2 A3 … An	Ai – произвольный исход
Pi	P1 P2 P3 … Pn	Pi – произвольная вероятность

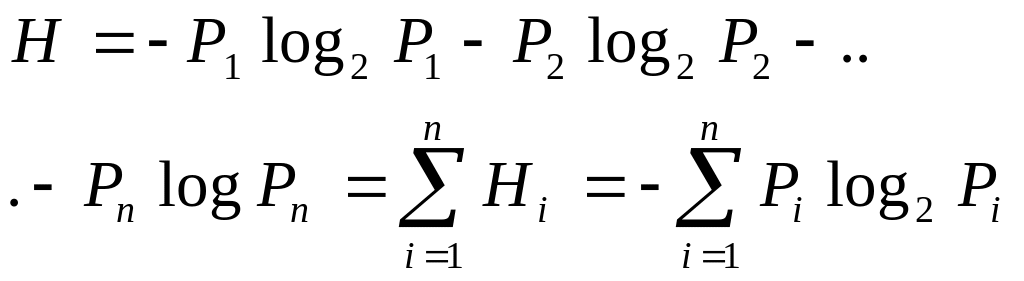
Воспользуемся -P_i log₂P_i (формула Хартли переделанная), которая дает возможность определения исхода события A_i: - формула Шеннона.

Здесь P_i м.б. разными. По смыслу эта величина H является средними значениями энтропии для всех опытов.

Докажем, что в случае равновероятных событий из формулы Шеннона можно получить формулу Хартли.

Положим P_i=P=const Нужно избавиться от P: P=1/n. Доказали: мы получили формулу Хартли, которая является частным случаем формулы Шеннона для некоторых условий.

EX:

Пусть некоторое сообщение х₁, х₂, х₃ появляются с вероятностью ½, 3/8, 1/8. Определить энтропию для сообщения и предложить систему кодирования для этого сообщения.

Используем формулу Шеннона:

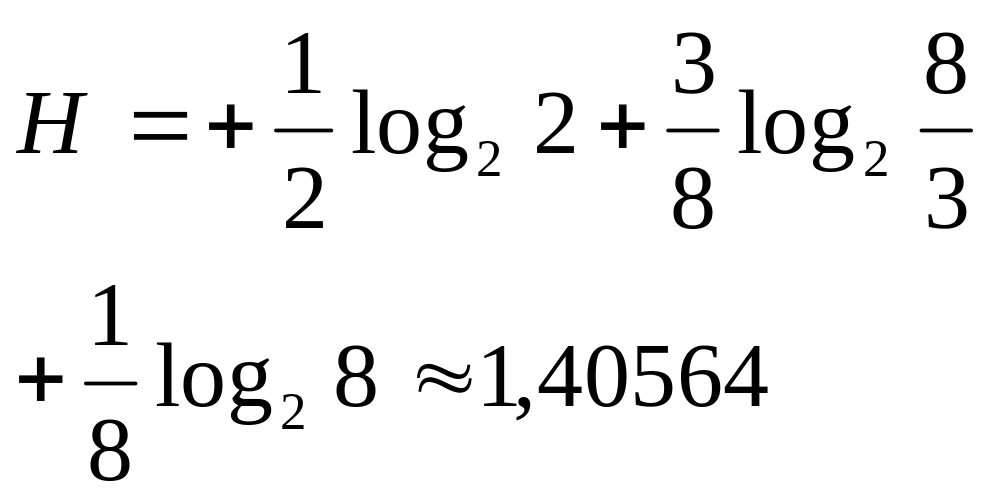
Это мера неопределенности для сообщения. Теоретическое значение, которое мы получим, является предельным, т.е. минимально возможным. На практике энтропия будет выше.

Обратимся ко второй части задачи. Определим систему кодирования. Если приходит сообщение х₁, то кодируем его 0, х₂ кодируем 10, х₃ кодируем 11. Посмотрим, как связана кодировка с полученной H.

х1	х2	х3
0	10	11
1/2	3/8	1/8

L= 1∙1/2+2∙3/8+2∙1/8=1/2+3/4+1/4=1,5 , где L-средняя длина сообщения.