Властивості перетворення Фур’є. Лінійність. Спектр згортки. Спектр добутку.

Хоча формула, що задає перетворення Фур'є, має ясний сенс тільки для функцій класу  , Перетворення Фур'є може бути визначено і для більш широкого класу функцій, і навіть узагальнених функцій. Це можливо завдяки ряду властивостей перетворення Фур'є:

• Перетворення Фур'є є лінійним оператором :

• Справедливо рівність Парсеваля : якщо   , То перетворення Фур'є зберігає L ₂ -Норму:

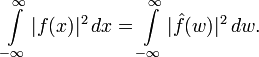
Ця властивість дозволяє по безперервності поширити визначення перетворення Фур'є на весь простір   . Рівність Парсеваля буде при цьому справедливо для всіх   .

• Формула звернення:

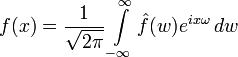
справедлива, якщо інтеграл в правій частині має сенс. Зокрема, це вірно, якщо функція f є досить гладкою. Якщо   , То формула також вірна, оскільки рівність Парсеваля дозволяє надати інтегралу в правій частині сенс за допомогою граничного переходу. Ця формула пояснює фізичний сенс перетворення Фур'є: права частина - (нескінченна) сума гармонійних коливань e ^i ω x з частотами ω , Амплітудами   і фазовими зрушеннями   відповідно.

• Теорема про згортку: якщо   , Тоді

 , Де

Ця формула може бути поширена і на випадок узагальнених функцій.

• Перетворення Фур'є і диференціювання. Якщ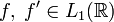о   , То

З цієї формули легко виводиться формула для n -ї похідної:

Формули вірні і у випадку узагальнених функцій.

• Перетворення Фур'є і зрушення.

Ця і попередня формула є окремими випадками теореми про згортку, так як зсув по аргументу - це згортка з зрушеної дельта-функцією δ (x - x ₀₎ , А диференціювання - згортка з похідною дельта-функції.

• Перетворення Фур'є і розтяг.

• Перетворення Фур'є узагальнених функцій. Перетворення Фур'є можна визначити для широкого класу узагальнених функцій. Визначимо спочатку простір гладких швидко убувають функцій ( простір Шварца):

Ключовою властивістю цього простору є те, що цей інваріантний підпростір по відношенню до перетворення Фур'є.

Методи перетворення і типи цап. Параметри. Критерії вибору.

Цифрово-аналоговий перетворювач є пристроєм, що здійснює трансформацію вхідного цифрового коду С в аналоговий вхідний сигнал А, найчастіше як напруга чи струм. Значення вхідного аналогового сигналу є функцією значення вхідного двійкового коду а_і та значення опорної напруги U_оп

A = k(a_n-12^-(n-1) + a_n-22^-(n-2) +…+ a₁2^-1 + a₀2⁰)U_оп,

де k – коефіцієнт пропорційності; a_n-1, a_n-2, …, a₁, a₀ – розряди двійкового коду. Найчастіше застосовуються два типи мережі опорів:

1. З ваговими опорами.

Якщо значення а_і-го біту двійкового коду дорівнює нулю, то відповідно струм І_і = 0. Якщо ж значення а_і = 1, то відповідно через опір R протече струм I_i = U_оп/R_i. операційний підсилювач є елементом, на вході якого здійснюється сумування струмів та їх перетворення у пропорційне значення напруги u по його виходу. Істотною вадою є значний діапазон опорів.

2. Драбина опорів типу R-2R.

ЦАП з драбиною опорів тиру R-2R потребують в два рази більше опорів, але їхні значення R і 2R відрізняються тільки в два рази. Напруга перетворення формулюється

u = U_оп(a_n-12^n-1 + a_n-22^n-2 +…+ a₀2⁰)/2ⁿ