
- •Умови Діріхле. Формальний запис ряду Фур’є.
- •Перетворення Фур’є.
- •Спектри періодичних та неперіодичних сигналів. Спектр дискретного сигналу.
- •Властивості перетворення Фур’є. Лінійність. Спектр згортки. Спектр добутку.
- •Методи перетворення і типи цап. Параметри. Критерії вибору.
- •Дискретизація за часом та квантування за рівнем. Похибки квантування.
- •Методи перетворення і типи ацп. Класифікація та параметри ацп.
Умови Діріхле. Формальний запис ряду Фур’є.
Теорема
Діріхле. Нехай на відрізку
![]() задана обмежена функція f (x), яка
задовольняє на цьому відрізку таким
двом умовам:
задана обмежена функція f (x), яка
задовольняє на цьому відрізку таким
двом умовам:
1. Функція f (x) неперервна або кусково-неперервна, тобто має на цьому відрізку лише кінцеве число точок розриву, причому тільки першого роду.
2. Функція f (x) монотонна або кусково-монотонна, тобто цей відрізок можна розбити на кінцеве число відрізків, на кожному з яких функція f (x) монотонно зростає, або убуває, або залишається постійною. Тоді така функція f (x) розкладається в відповідний їй тригонометричний ряд Фур'є, який сходиться на цьому відрізку, причому:
1) в кожній точці х = х0 неперервності функції f(x) сума ряду S(x) рівна значенню функції f(x) в цій точці:
S (x0) = f (x0)
2) в кожній точці х = х1 розриву функції f(x) сума ряду рівна середньому арифметичному односторонніх границь функції в цій точці:
![]()
3) в
точках
![]() и
и
![]() (на границях відрізка) сума ряду рівна
середньому арифметичному правої границі
f(x) в точці
і лівої границі f(x) в точці
:
(на границях відрізка) сума ряду рівна
середньому арифметичному правої границі
f(x) в точці
і лівої границі f(x) в точці
:
![]()
4) на всякому кінцевому відрізку, вільному від точок розриву функції f(x), ряд рівномірно сходиться до f(x).
Теорема Діріхле дає достатні умови розкладу функції f(x) в тригонометричний ряд. Умови 1 і 2 теореми називаються умовами Діріхле. Ряд Фур'є дозволяє вивчати періодичні (неперіодичні) функції, розкладаючи їх на компоненти. Змінні струми і напруги, зміщення, швидкість і прискорення кривошипно-шатунних механізмів і акустичні хвилі - це типові практичні приклади застосування періодичних функцій в інженерних розрахунках. Розкладання в ряд Фур'є грунтується на припущенні, що всі мають практичне значення функції в інтервалі -π≤x≤ π можна виразити у вигляді збіжних тригонометричних рядів (ряд вважається збіжним, якщо сходиться послідовність часткових сум, складених з його членів):
f(x)=ao+ a1cosx+a2cos2x+a3cos3x+...+b1sinx+b2sin2x+b3sin3x+...,
де ao, a1,a2,...,b1,b2,.. – дійсні константи, тобто
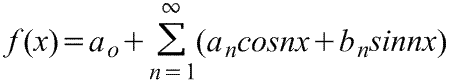 (1)
(1)
Де для діапазону від-π до π коефіцієнти ряду Фур'є розраховуються за формулами:

Коефіцієнти ao, an і bn називаються коефіцієнтами Фур'є, і якщо їх можна знайти, то ряд (1) називається рядом Фур'є, відповідним функції f(x). Для ряду (1) член (a1cosx + b1sinx) називається першою або основною гармонікою.
Перетворення Фур’є.
Перетворення Фур'є - перетворення функції, що перетворює її в сукупність частотних складових. Більш точно, перетворення Фур'є - це інтегральне перетворення, яке розкладає вихідну функцію на базисні функції, в якості яких виступають синусоїдальні функції, тобто представляє вихідну функцію у вигляді інтеграла синусоїд різної частоти, амплітуди і фази. Перетворення названо по імені Жана Фур'є. Перетворення Фур'є використовується в багатьох галузях науки - у фізиці, теорії чисел, комбінаторики, обробці сигналів, теорії ймовірності, статистиці, криптографії, акустиці, океанології, оптиці, геометрії, і багатьох інших. (В обробці сигналів і пов'язаних областях перетворення Фур'є звичайно розглядається як декомпозиція сигналу на частоти і амплітуди.) Багаті можливості застосування грунтуються на декількох корисних властивостях перетворення:
Перетворення є лінійними операторами і, з відповідною нормалізацією, також є унітарними (властивість, відоме як теорема Парсеваля або, в більш загальному випадку як теорема Планшереля, або в найбільш загальному як дуалізм Понтрягіна).
Перетворення оборотні, причому зворотне перетворення має практично таку ж форму, як і пряме перетворення.
Синусоїдальні базисні функції є власними функціями диференціювання, що означає, що дане подання перетворює лінійні диференціальні рівняння з постійними коефіцієнтами у звичайні алгебраїчні. (Наприклад, в лінійній стаціонарної системі частота - консервативна величина, тому поведінка на кожній частоті може вирішуватися незалежно.)
По теоремі про згортку, перетворення Фур'є перетворює складну операцію згортки в просте множення, що означає, що вони забезпечують ефективний спосіб обчислення заснованих на згортку операцій, таких як множення многочленів і множення великих чисел.
Дискретна версія перетворення Фур'є може швидко розраховуватися на комп'ютерах, використовуючи алгоритм швидкого перетворення Фур'є
Найбільш
часто термін «перетворення Фур'є»
використовують для позначення
безперервного перетворення Фур'є, що
представляє будь-яку квадратично-інтегрвану
функцію
![]() як суму (інтеграл Фур'є) комплексних
показових функцій з кутовими частотами
як суму (інтеграл Фур'є) комплексних
показових функцій з кутовими частотами
![]() і комплексними амплітудами
і комплексними амплітудами
![]() .
Перетворення має кілька форм, що
відрізняються постійними коефіцієнтами.
.
Перетворення має кілька форм, що
відрізняються постійними коефіцієнтами.

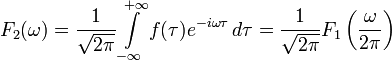
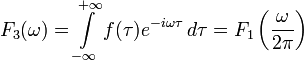 ,
,
де
![]() .
У різних областях науки і техніки можуть
переважати різні форми (тому іноді треба
уточнювати визначення).
.
У різних областях науки і техніки можуть
переважати різні форми (тому іноді треба
уточнювати визначення).
Безперервне
перетворення саме фактично є узагальненням
більш ранньої ідеї рядів Фур'є, які
визначені для періодичних функцій або
функцій, що існують на обмеженій області
![]() (з періодом
(з періодом
![]() )
,
і представляють ці функції як ряди
синусоїд:
)
,
і представляють ці функції як ряди
синусоїд:
![]() ,
,
де
![]() - комплексна амплітуда. Або ряд Фур'є
часто записується як:
- комплексна амплітуда. Або ряд Фур'є
часто записується як:
![]() ,
,
де
![]() і
і
![]() - (дійсні) амплітуди ряду Фур'є.
- (дійсні) амплітуди ряду Фур'є.
Для
використання в комп'ютерах, як для
наукових розрахунків, так і для цифрової
обробки сигналів, необхідно мати функції
![]() ,
які визначені на дискретній множині
точок замість безперервної області,
знову періодичній або обмеженій. У цьому
випадку використовується дискретне
перетворення Фур'є, яке представляє
як суму синусоїд:
,
які визначені на дискретній множині
точок замість безперервної області,
знову періодичній або обмеженій. У цьому
випадку використовується дискретне
перетворення Фур'є, яке представляє
як суму синусоїд:
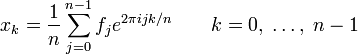 ,
,
де
![]() - амплітуди Фур'є. Хоча безпосереднє
застосування цієї формули вимагає
операцій, цей розрахунок може бути
зроблений за операцій використовуючи
алгоритм швидкого перетворення Фур'є,
що робить перетворення Фур'є практично
важливою операцією на комп'ютері.
- амплітуди Фур'є. Хоча безпосереднє
застосування цієї формули вимагає
операцій, цей розрахунок може бути
зроблений за операцій використовуючи
алгоритм швидкого перетворення Фур'є,
що робить перетворення Фур'є практично
важливою операцією на комп'ютері.
