Как вычислить объем тела вращения?

Объем тела вращения можно вычислить по формуле:

В формуле перед интегралом обязательно присутствует число  . Так повелось – всё, что в жизни крутится, связано с этой константой.

Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.

Функция  … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы   сверху. Это и есть та функция, которая подразумевается в формуле.

В практических заданиях плоская фигура иногда может располагаться и ниже оси  . Это ничего не меняет – функция в формуле возводится в квадрат:  , таким образом объем тела вращения всегда неотрицателен, что весьма логично.

Вычислим объем тела вращения, используя данную формулу:

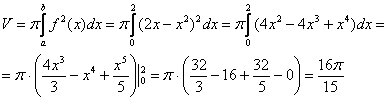
Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.

Ответ: 

В ответе нужно обязательно указать размерность – кубические единицы  . То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические единицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.

Пример 2

Найти объем тела, образованного вращением вокруг оси   фигуры, ограниченной линиями  ,  , 

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Рассмотрим две более сложные задачи, которые тоже часто встречаются на практике.

Пример 3

Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями  ,  ,   и 

Решение: Изобразим на чертеже плоскую фигуру, ограниченную линиями  ,  ,  ,  , не забывая при этом, что уравнение   задает ось  :

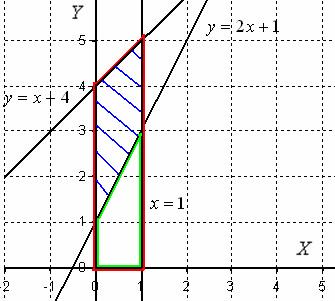
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси   получается такой сюрреалистический бублик с четырьмя углами.

Объем тела вращения вычислим как разность объемов тел.

Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси   получается усеченный конус. Обозначим объем этого усеченного конуса через  .

Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси  , то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через  .

И, очевидно, разность объемов   – в точности объем нашего «бублика».

Используем стандартную формулу для нахождения объема тела вращения: 

1) Фигура, обведенная красным цветом ограничена сверху прямой  , поэтому:

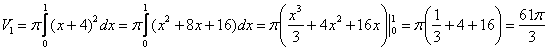
2) Фигура, обведенная зеленым цветом ограничена сверху прямой  , поэтому:

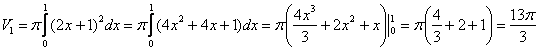
3) Объем искомого тела вращения: 

Ответ: 

Любопытно, что в данном случае решение можно проверить, используя школьную формулу для вычисления объема усеченного конуса.

Само решение чаще оформляют короче, примерно в таком духе:

Теперь немного отдохнем, и расскажу о геометрических иллюзиях.

У людей часто возникают иллюзии, связанная с объемами, которую подметил еще Перельман (не тот) в книге Занимательная геометрия. Посмотрите на плоскую фигуру в прорешанной задаче – она вроде бы невелика по площади, а объем тела вращения составляет чуть более 50 кубических единиц, что кажется слишком большим. Кстати, среднестатистический человек за всю свою жизнь выпивает жидкость объемом с комнату площадью 18 квадратных метров, что, наоборот, кажется слишком маленьким объемом.

Вообще, система образования в СССР действительно была самой лучшей. Та же книга Перельмана, написанная им еще в 1950 году, очень хорошо развивает, как сказал юморист, соображаловку и учит искать оригинальные нестандартные решения проблем. Недавно с большим интересом перечитал некоторые главы, рекомендую, доступно даже для гуманитариев. Нет, не нужно улыбаться, что я предложил беспонтовое времяпровождение, эрудиция и широкий кругозор в общении – отличная штука.

После лирического отступления как раз уместно решить творческое задание:

Пример 4

Вычислить объем тела, образованного вращением относительно оси   плоской фигуры, ограниченной линиями  ,  , где  .

Это пример для самостоятельного решения. Обратите внимание, что все дела происходят в полосе  , иными словами, фактически даны готовые пределы интегрирования.  Правильно начертите графики тригонометрических функций, напомню материал урока огеометрических преобразованиях графиков: если аргумент делится на два:  , то графики растягиваются по оси   в два раза. Желательно найти хотя бы 3-4 точки по тригонометрическим таблицам, чтобы точнее выполнить чертеж. Полное решение и ответ в конце урока. Кстати, задание можно решить рационально и не очень рационально.