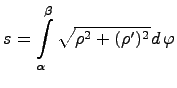- •Функции двух и трех переменных как функции точки
- •Геометрическое изображение функции двух переменных с помощью поверхностей и линий уровня.
- •Предел функции. Непрерывность в точке и в области.
- •Частные производные функции нескольких переменных, геометрический смысл частных производных функции двух переменных.
- •Полный дифференциал функции нескольких переменных.
- •3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной ( , либо какой-нибудь другой), по которой ведется дифференцирование.
- •3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной ( , либо какой-нибудь другой), по которой ведется дифференцирование.
- •Частные производные высших порядков.
- •Экстремум функции двух переменных. Необходимые условия экстремума.
- •Достаточные условия экстремума функции двух переменных.
- •Наибольшее и наименьшее значение функций в замкнутой ограниченной области.
- •Условный экстремум функции двух переменных. Экономический смысл множителей Лангранжа.
- •Первообразная. Неопределенный интеграл.
- •Некоторые дополнительные интегралы
- •Основные свойства неопределенного интеграла.
- •Метод замены переменной в неопределенном интеграле.
- •Метод интегрирования по частям.
- •Интегралы от логарифмов
- •Интегралы от экспоненты, умноженной на многочлен
- •Интегралы от тригонометрических функций, умноженных на многочлен
- •Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен
- •Интегралы от некоторых функций, содержащих трехчлен.
- •Интегрирование рациональных дробей.
- •Интегрирование иррациональных функций.
- •Интегралы от корней. Типовые методы и приемы решения
- •Интегрирование биномиальных интегралов
- •2) Случай второй
- •Интегрирование тригонометрических функций.
- •Использование тригонометрических формул
- •Понижение степени подынтегральной функции
- •Метод замены переменной
- •Универсальная тригонометрическая подстановка
- •См. Конспект
- •См. Конспект
- •Определение определенного интеграла. Основные свойства.
- •Определение
- •Обозначения
- •Свойства
- •Геометрический смысл
- •Теорема об интеграле с переменным верхним пределом.
- •Формула Ньютона-Лейбница.
- •Замена переменной в определенном интеграле.
- •Интегрирование по частям при вычислении определенного интеграла. Метод интегрирования по частям в определенном интеграле
- •Вычисление площадей плоских фигур в прямоугольных координатах.
- •Вычисление площади плоских фигур в полярных координатах.
- •Площадь криволинейного сектора - вывод формулы.
- •Примеры вычисления площади криволинейного сектора.
- •Вычисление длины дуги плоской кривой.
- •Вычисление объема тела по площадям параллельных сечений.
- •Объем тела вращения. Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
- •Как вычислить объем тела вращения?
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
- •Интегралы с бесконечными пределами интегрирования.
- •Несобственный интеграл с бесконечным пределом (ами) интегрирования
- •Несобственные интегралы от неограниченных функций
- •Интегралы от неограниченных функций.
- •Признаки сходимости несобственных интегралов.
- •Обыкновенные дифференциальные уравнения (основные понятия).
- •Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши (формулировка).
- •Дифференциальные уравнения с разделяющимися переменными.
- •Дифференциальные уравнения с однородными функциями.
- •Как решить однородное дифференциальное уравнение?
- •Линейные дифференциальные уравнения первого порядка и уравнения Бернулли.
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка.
- •Метод повторного интегрирования правой части
- •В дифференциальном уравнении в явном виде отсутствует функция
- •В дифференциальном уравнении в явном виде отсутствует независимая переменная
- •Линейные однородные уравнения n-го порядка, свойства их решений.
- •Теорема о структуре общего решения линейного однородного дифференциального уравнения.
- •Теорема о структуре общего решения линейного неоднородного дифференциального уравнения.
- •Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Характеристическое уравнение имеет два различных действительных корня
- •Характеристическое уравнение имеет два кратных действительных корня
- •Характеристическое уравнение имеет сопряженные комплексные корни
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида.
- •Общее решение неоднородного дифференциального уравнения:
Примеры вычисления площади криволинейного сектора.
Разберемся с вычислением площади криволинейного сектора, заданного в полярной системе координат, при решении примеров.
Пример.
Вычислить
в полярных координатах площадь плоской
фигуры, ограниченной линией ![]() и
лучами
и
лучами ![]() .
.
Решение.
Функция
положительна
и непрерывна на отрезке 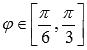 .
Для наглядности изобразим фигуру в
полярной системе координат.
.
Для наглядности изобразим фигуру в
полярной системе координат.
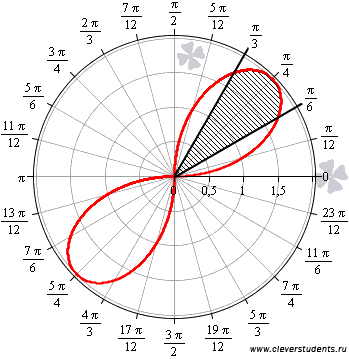
Эта
фигура является криволинейным сектором,
и мы сразу можем применить соответствующую
формулу для нахождения его площади:
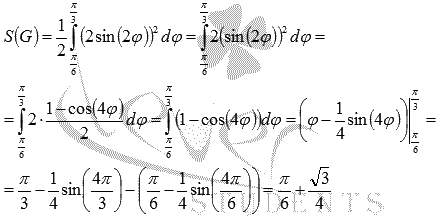
Когда
заданы два луча ![]() ,
ограничивающие фигуру, не приходится
думать о пределах интегрирования при
вычислении площади. Однако более
распространены задачи, где фигуру
ограничивает лишь кривая
.
Как же в этом случае применять формулу
,
ограничивающие фигуру, не приходится
думать о пределах интегрирования при
вычислении площади. Однако более
распространены задачи, где фигуру
ограничивает лишь кривая
.
Как же в этом случае применять формулу ![]() ?
?
В
таких примерах сначала следует решить
неравенство ![]() ,
откуда становятся видны пределы
интегрирования.
,
откуда становятся видны пределы
интегрирования.
Замечание.
Так мы поступаем, если считаем функцию неотрицательной, в противном случае ориентируемся только на область определения и период функции.
Разберем на примерах.
Пример.
Вычислить
площадь фигуры, ограниченной кривой в
полярных координатах ![]() .
.
Решение.
Функция
определена для всех действительных
значений аргумента. Решим неравенство ![]() :
:
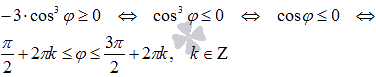
Построим
функцию в полярных координатах на
отрезке ![]() (при k=0).
Для других значений k в
силу периодичности косинуса мы будем
получать ту же самую кривую.
(при k=0).
Для других значений k в
силу периодичности косинуса мы будем
получать ту же самую кривую.
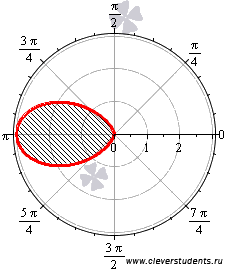
Применяем
формулу для вычисления площади фигуры
в полярных координатах. В качестве
нижнего и верхнего предела можно
брать ![]() и
и ![]() соответственно
для любого целого значения k.
соответственно
для любого целого значения k.
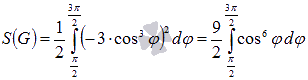
Осталось
вычислить полученный определенный
интеграл. Справиться с этой задачей нам
поможет формула
Ньютона-Лейбница.
А первообразную для формулы Ньютона-Лейбница
найдем, используя рекуррентную
формулу вида ![]() ,
где
,
где ![]() .
.
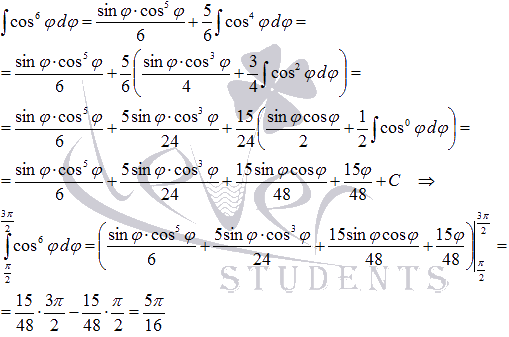
Таким
образом, искомая площадь фигуры,
ограниченной линией в полярной системе
координат, равна 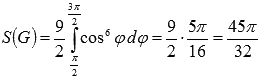 .
.
В полярной системе координат можно задать множество кривых, по форме напоминающих листья клевера или лепестки розы. Лепестки фигур, ограниченных такими кривыми, часто одинаковы. Поэтому, когда стоит задача вычислить площадь такой фигуры, находится площадь одного лепестка и умножается на их количество.
Пример.
Вычислить
в полярных координатах площадь плоской
фигуры, ограниченной линией ![]() .
.
Решение.
Эта
функция неотрицательна для любого ![]() из
области определения. Найдем область
определения:
из
области определения. Найдем область
определения:
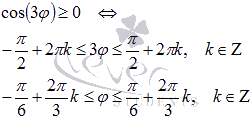
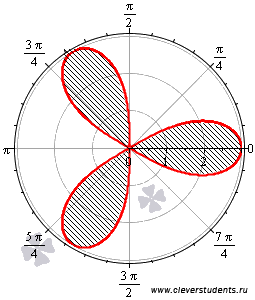
Таким
образом, период функции
равен ![]() ,
то есть, фигура будет состоять из трех
равных областей. Построим ее.
,
то есть, фигура будет состоять из трех
равных областей. Построим ее.
Вычислим
площадь одного лепестка, расположенного
на интервале ![]() (приk=1):
(приk=1):
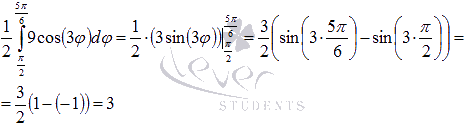
Таким образом, площадь всей фигуры будет равна утроенному значению, то есть, девяти.
Аналогично находятся площади схожих фигур, например, лемнискаты Бернулли.
Вычисление длины дуги плоской кривой.
Пусть
известна функция ![]() и
требуется найти длину дуги, заданной
функцией
,
где
и
требуется найти длину дуги, заданной
функцией
,
где ![]() .
.
Для
определения длины дуги ![]() необходимо
вычислить определенный
интеграл:
необходимо
вычислить определенный
интеграл:
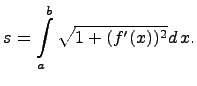
Рассмотрим случай параметрического задания кривой:
![]()
где ![]() .
В этом случае для определения длина
дуги
вычисляется определенный
интеграл:
.
В этом случае для определения длина
дуги
вычисляется определенный
интеграл:
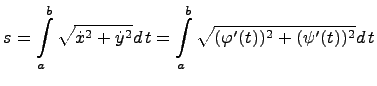
Рассмотрим
случай, когда кривая задается в полярных
координатах ![]() где
где ![]() .
Тогда для определения длины
дуги
вычисляется
следующий определенный
интеграл:
.
Тогда для определения длины
дуги
вычисляется
следующий определенный
интеграл: