Примеры.

Далее через обозначено одно из полей или .

• Евклидовы пространства 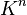с евклидовой нормой, определяемой для 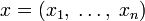как 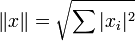, являются банаховыми пространствами.

• Пространство всех непрерывных функций 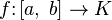, определённых на закрытом интервале будет банаховым пространством, если мы определим его норму как 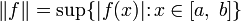. Такая функция будет нормой, так как непрерывные функции на закрытом интервале являются ограниченными. Пространство с такой нормой является полным, а полученное банахово пространство обозначается как 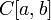. 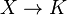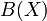Этот пример можно обобщить к пространству всех непрерывных функций , где  — компактное пространство, или к пространству всех ограниченных непрерывных функций , где  — любое топологическое пространство, или даже к пространству всех ограниченных функций , где  — любое множество. Во всех этих примерах мы можем перемножать функции, оставаясь в том же самом пространстве: все эти примеры являются банаховыми алгебрами.

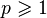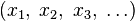• Если  — вещественное число, то пространство всех бесконечных последовательностей элементов из , таких что ряд 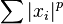сходится, является банаховым относительно нормы, равной корню степени из суммы этого ряда, и обозначается .

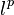• Банахово пространство 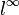состоит из всех ограниченных последовательностей элементов из ; норма такой последовательности определяется как точная верхняя грань абсолютных величин (модулей) элементов последовательности.

• Снова, если  — вещественное число, можно рассматривать все функции интегрируемыми по Лебегу. Корень степени этого интеграла определим как норму . Само собой, это пространство не будет банаховым, поскольку есть ненулевые функции, чья норма будет равна нулю. Определим отношение эквивалентности следующим образом: и 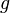эквивалентны тогда и только тогда, когда норма 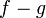равна нулю. Множество классов эквивалентности тогда является банаховым пространством; оно обозначается как 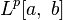. Важно использовать именно интеграл Лебега, а не интеграл Римана, поскольку интеграл Римана не порождает полное пространство. Эти примеры можно обобщить. См., например, 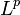-пространства.

• Если и  — банаховы пространства, то можно составить их прямую сумму , которая опять-таки будет банаховым пространством. Можно и обобщить этот пример к прямой сумме произвольно большого числа банаховых пространств.

• Если  — замкнутое подпространство банахова пространства , то факторпространство 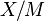снова является банаховым.

• Любое гильбертово пространство тоже является банаховым. Обратное неверно.

• Если и  — банаховы пространства над одним полем , тогда множество непрерывных -линейных отображений 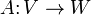обозначается 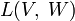. Заметим, что в бесконечномерных пространствах не все линейные отображения автоматически являются непрерывными.  — векторное пространство, и, если норма задана как 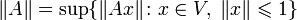, является также и банаховым.

  • Пространство 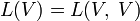представляет собой унитарную банахову алгебру; операция умножения в ней задаётся как композиция линейных отображений.