Примеры.
Дискретная метрика:
,
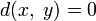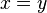если
,
и
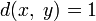во
всех остальных случаях.Вещественные числа с функцией расстояния
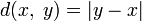и
евклидово пространство являются полными
метрическими пространствами.
Пусть
—
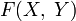пространство непрерывных и ограниченных
отображений из топологического
пространства
в
метрическое пространство
.
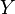Расстояние между двумя отображениям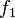и
и
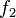из
этого пространства определяется как
Сходимость отображений по этой метрике равнозначна их равномерной сходимости на всём пространстве .
В частном случае, когда
—
компактное пространство,
—
числовая прямая, получается пространство
всех
непрерывных функций на пространстве X
с метрикой равномерной сходимости.
Пусть
,
,
—
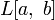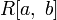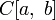пространства функций на отрезке
,
соответственно интегрируемых по Лебегу,
интегрируемых по Риману, и непрерывных.
В них расстояние можно определить по
формуле:
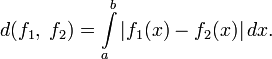
Для того, чтобы эта функция стала метрикой, в первых двух пространствах необходимо отождествить функции, отличающиеся на множестве меры 0. В противном случае эта функция будет всего лишь полуметрикой. (В пространстве функций, непрерывных на отрезке, функции, отличающиеся на множестве меры 0, и так совпадают.)
В пространстве k раз непрерывно дифференцируемых функций
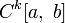метрика
вводится по формуле:
где
—
метрика равномерной сходимости на
(см.
выше).
Любое нормированное пространство можно превратить в метрическое, определив функцию расстояния
.
Конечномерные пространства такого типа называются пространством Минковского;
в случае если размерность равна двум то плоскостью Минковского.
Любое связное риманово многообразие
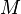можно
превратить в метрическое пространство,
определив расстояние как точную нижнюю
грань длин путей, соединяющих пару
точек.Множество вершин любого связного графа можно превратить в метрическое пространство, определив расстояние как минимальное число рёбер в пути, соединяющем вершины. Более общо: если каждому рёбру графа приписать положительное число (длину ребра), расстояние между вершинами можно определить как минимальную сумму длин рёбер вдоль любых путей из одной вершины в другую.
Частным случаем предыдущего примера является так называемая французская железнодорожная метрика — пример, который нередко приводят в качестве примера метрики, не порождённой нормой.
Множество компактных подмножеств
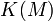любого
метрического пространства
можно
превратить в метрическое пространство,
определив расстояние с помощью так
называемой метрики Хаусдорфа. В этой
метрике два подмножества близки друг
к другу, если для любой точки одного
множества можно найти близкую точку в
другом подмножестве. Вот точное
определение:
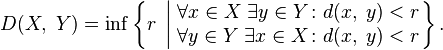
Множество всех компактных метрических пространств (с точностью до изометрии) можно превратить в метрическое пространство, определив расстояние с помощью так называемой метрики Громова — Хаусдорфа.
Банаховы и гильбертовы пространства. Банахово пространство.
Ба́нахово пространство — нормированное векторное пространство, полное по метрике, порождённой нормой. Основной объект изучения функционального анализа. Названо по имени польского математика Стефана Банаха.