Интеграл Лебега.

Интеграл Лебе́га — это обобщение интеграла Римана на более широкий класс функций. Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла равны. Однако существует большой класс функций, определённых на отрезке и интегрируемых по Лебегу, но неинтегрируемых по Риману. Также интеграл Лебега может иметь смысл для функций, заданных на произвольных множествах.

Идея построения интеграла Лебега состоит в том, что вместо разбиения области определения подынтегральной функции на части и составления потом интегральной суммы из значений функции на этих частях, на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.

Определение интеграла Лебега.

Интеграл Лебега определяют пошагово, переходя от более простых функций к сложным. Будем считать, что дано пространство с мерой , и на нем определена борелевская функция .

Определение 1. Пусть  — индикатор некоторого измеримого множества, то есть , где . Тогда интеграл Лебега функции по определению:

Определение 2. Пусть  — простая функция, то есть , где , а  — конечное разбиение на измеримые множества. Тогда

.

Определение 3. Пусть теперь  — неотрицательная функция, то есть . Рассмотрим все простые функции , такие что . Обозначим это семейство . Для каждой функции из этого семейства уже определён интеграл Лебега. Тогда интеграл от задаётся формулой:

Наконец, если функция произвольного знака, то её можно представить в виде разности двух неотрицательных функций. Действительно, легко видеть, что:

где

.

Определение 4. Пусть  — произвольная измеримая функция. Тогда ее интеграл задаётся формулой:

.

Определение 5. Пусть наконец произвольное измеримое множество. Тогда по определению

,

где  — индикатор-функция множества .

Нормированные пространства. Норма. Примеры. Нормированное пространство.

В трёхмерном пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:

1. Длина нуль-вектора, 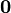, равна нулю; длина любого другого вектора положительна.

2. Умножение вектора на положительное число во столько же раз увеличивает длину вектора.

3. Действует неравенство треугольника.

Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным пространством.

Определение.

Полунормированным векторным пространством называется пара , где — векторное пространство, а — полунорма в .

Нормированным векторным пространством называется пара , где — векторное пространство, а — норма в .

Часто обозначение и опускают и пишут просто , если из контекста ясно, какая норма или полунорма имеется в виду.

Топологическая структура.

Для любого полунормированного векторного пространства мы можем задать расстояние между двумя векторами и как . Такое полунормированное пространство с определённым таким образом расстоянием называется полунормированным метрическим пространством, в котором мы можем определить такие понятия как непрерывность и сходимость. Более абстрактно, любое полунормированное векторное пространство является топологическим векторным пространством и, таким образом, несёт топологическую структуру, порождённую полунормой.

Особый интерес представляют полные нормированные пространства, называемые банаховыми пространствами. Любое нормированное векторное пространство находится как плотное подпространство внутри банахова пространства, а это банахово пространство однозначно определяется пространством и называется пополнением пространства .

Все нормы в конечномерном векторном пространстве эквивалентны с топологической точки зрения, так как они порождают одну и ту же топологию. А так как любое евклидово пространство полно, мы можем сделать вывод, что все конечномерные векторные пространства являются банаховыми пространствами. Нормированное векторное пространство конечномерно тогда и только тогда, когда единичный шар компактен, что может быть тогда и только тогда, когда локально-компактно.

Топология полунормированного вектора обладает несколькими интересными свойствами. Взяв окрестностную систему около , мы можем построить все остальные окрестностные системы как

с помощью

Более того, существует базис окрестностей для , состоящий из поглощающих и выпуклых множеств. Так как это свойство очень полезно в функциональном анализе, обобщения нормированных векторных пространств с этим свойством изучаются как локально-выпуклые пространства.

Линейные отображения и двойственные пространства.

Наиболее важными отображениями между двумя нормированными векторными пространствами являются непрерывные линейные отображения. Нормированные векторные пространства с такими отображениями образуют категорию.

Норма — это непрерывная функция в своём векторном пространстве. Все линейные отображения между конечномерными векторными пространствами также непрерывны.

Изометрией между двумя нормированными векторными пространствами называется линейное отображение , сохраняющее норму (то есть для всех векторов ). Изометрии всегда непрерывны и инъективны. Сюръективная изометрия между нормированными векторными пространствами и называется изометрическим изоморфизмом. Изометрически изоморфные нормированные векторные пространства можно считать равноправными для практически любых целей.

Говоря о нормированных векторных пространствах мы должны упомянуть двойственные пространства. Двойственное пространство нормированного векторного пространства — это пространство всех непрерывных линейных отображений из на основное поле (поле комплексных или действительных чисел), а такие линейные отображения называются функционалами. Норма функционала определяется как

Введение такой нормы превращает в нормированное векторное пространство. Важной теоремой о непрерывных линейных функционалах в нормированных векторных пространствах является теорема Хана — Банаха.