Следствия аксиом линейного пространства.

1. В линейном пространстве существует единственный нулевой вектор.

2. В линейном пространстве для любого вектора 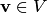существует единственный противоположный вектор .

3. Произведение произвольного вектора пространства на число нуль равно нулевому вектору, т.е. .

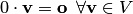4. Произведение нулевого вектора на любое число равно нулевому вектору, т.е 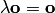для любого числа .

5. Вектор, противоположный данному вектору, равен произведению данного вектора на число (-1), т.е. .

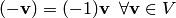6. В выражениях вида 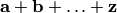(сумма конечного числа векторов) или 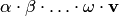(произведение вектора на конечное число множителей) можно расставлять скобки в любом порядке, либо вообще не указывать.

Докажем, например, первые два свойства. Единственность нулевого вектора. Если и — два нулевых вектора, то по аксиоме 3 получаем два равенства: или , левые части которых равны по аксиоме 1. Следовательно, равны и правые части, т.е. . Единственность противоположного вектора. Если вектор имеет два противоположных вектора и , то по аксиомам 2, 3,4 получаем их равенство:

Остальные свойства доказываются аналогично.

Операторы. Линейные операторы. Матрица оператора. Базис. Линейные операторы.

Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.

Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.

Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.

Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо:

A(u + v) = A(u ) + A(v) ,  A(α·u) = α· A(u).

Множество векторов y линейного пространства Y, для каждого из которых существует такой вектор x из линейного пространства X, что y = A(x) называется образом оператора A:

Im(A) = {y | y = A(x), x∈ X}, Im(A) ⊆ Y.

Образ линейного оператора — линейное подпространство пространства Y. Размерность образа линейного оператора называется рангом оператора: rank A = dim (Im A); rank A = rang A = rg A = Rg A.

Матрица оператора.

Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y .

В этих пространствах определены базисы e = {e₁, ..., e_n} и f = {f₁, ..., f_m}.

Пусть A(e_i ) = a_1i·f₁ + a_2i·f₂ + ...+ a_mi·f_m — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2, ..., n.

Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {a_ij}= {A(e_j )_i}:

Координаты образа y = A(x) и прообраза x связаны соотношеннием:

y = A· x,

Базис линейного пространства.

Система векторов линейного пространства L образует базис в L если эта система векторов упорядочена, линейно независима и любой вектор из  L линейно выражается через векторы системы.

Иными словами, линейно независимая упорядоченная система векторов e₁, ..., e_n образует базис в L если любой вектор x из L может быть представлен в виде

x = С₁·e₁+С₂·e₂+ ...+С_n· e_n.

Можно определить базис иначе.

Любая упорядоченная линейно независимая система e₁, ..., e_n векторов n-мерного линейного пространства L_n образует базис этого пространства.

Поскольку n, размерность пространства L_n— максимальное количество линейно независимых векторов пространства, то система векторов x, e₁, ..., e_n линейно зависима и, следовательно, вектор x линейно выражается через векторы e₁, ..., e_n:

x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n.

Такое разложение вектора по базису единственно.