Ортонормированный базис.

Ортонормированная система, состоящая из n векторов n-мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.

Если e₁, e₂, ..., e_n — ортонормированный базис n-мерного евклидова пространства и

x = x₁e₁ + x₂e₂ + ... + x_ne_n — разложение вектора x по этому базису, то координаты x_i вектора x в ортонормированном базисе вычисляются по формулам x_i =(x, e_i), i = 1, 2, ..., n.

В любом конечномерном евклидовом пространстве существует ортонормированный базис. 

Любую ортонормированную систему векторов конечномерного евклидова пространства можно дополнить до ортонормированного базиса. 

Процесс Грама ― Шмидта

Процесс Грама (англ.) ― Шмидта — это один из алгоритмов, в которых на основе счётного множества линейно независимых векторов строится множество ортогональных векторов или ортонормированных векторов , причём так, что каждый вектор или может быть выражен линейн Пусть имеются линейно независимые векторы .

Определим оператор проекции следующим образом:

где  — скалярное произведение векторов и . Этот оператор проецирует вектор ортогонально на вектор .

Классический процесс Грама — Шмидта выполняется следующим образом:

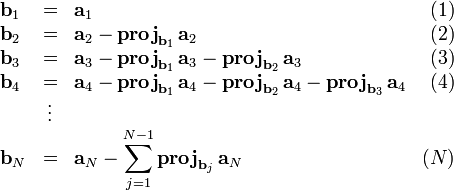
На основе каждого вектора может быть получен нормированный вектор: (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).

Результаты процесса Грама — Шмидта:

 — система ортогональных векторов либо

 — система ортонормированных векторов.

Вычисление носит название ортогонализации Грама — Шмидта, а  — ортонормализации Грама — Шмидта.

ой комбинацией векторов .