19. Сила Лоренца и сила Ампера. Действие магнитного поля на проводник с током.

Сила Ампера.

Действие магнитного поля на проводник с током

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.

Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: 

F=B^.I^.ℓ^. sin  — закон Ампера.

Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.

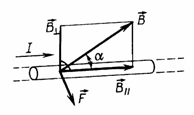
Направление силы Лоренца (правило левой руки)Направление F определяется по правилу левой руки: вектор Fперпендикулярен векторам В и v..

Правило левой руки сформулировано для положительной частицы. Сила, действующая на отрицательный заряд будет направлена в противоположную сторону по сравнению сположительным.

Если вектор v частицы перпендикулярен вектору В, то частица описывает траекторию в виде окружности: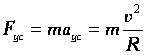   

Роль центростремительной силы играет сила Лоренца: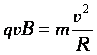 

При этом радиус окружности:  ,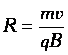

а период обращения   не зависит от радиуса окружности!

Если вектор скорости и частицы не перпендикулярен В, то частица описывает траекторию в виде винтовой линии (спирали).

20. Магнитное поле в веществе. Классическая теория диамагнетизма

Физическая величина, показывающая, во сколько раз индукция   магнитного поля в однородной среде отличается по модулю от индукции   магнитного поля в вакууме, называется магнитной проницаемостью: 

Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10^–5, у хлористого железа (FeCl₃) μ – 1 ≈ 2,5·10^–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10^–6), вода (μ – 1 ≈ –9·10^–6), висмут (μ – 1 ≈ –1,7·10^–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются

Диамагнетиками являются инертные газы, многие органические соединения, некоторые металлы ( ,  , ,  ,  ,  ) смолы, молекулярный водород, стекло, мрамор и др.

Причиной диамагнетизма по классической теории является процессия орбиты вокруг внешнего магнитного поля. Эта процессия вызывает изменение угловой скорости электрона на велечину

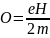, где

где означают абсолютную величину заряда и массы электрона, – напряженность внешнего магнитного поля. Но, с другой стороны, электрон, движущийся по орбите, может быть рассматриваем как электрический ток, текущий по замкнутому контуру.

Магнитный момент такого тока будет равен

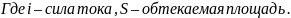
Если – время обращения электрона, то в нашем случае (3)

Обозначая угловую скорость электрона через , получаемя (4)

Нас интересует дополнительный магнитный момент (5)

Обозначая через среднее по времени значение квадрата проекции радиуса электронной орбиты на плоскость, перпендикулярную к направлению внешнего магнитного поля, можем написать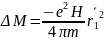 (6)

Если через обозначим квадрат среднего радиуса орбиты, то для сферически симметричного атома можно принять

Для атома, имеющего электронов, . (7)

И окончательно, для атомной диамагнитной восприимчивости получаем формулу Ланжевена-Паули , (8)

Где – число Авогадро.

21. Магнитное поле в веществе. Классическая теория парамагнетизма

Физическая величина, показывающая, во сколько раз индукция   магнитного поля в однородной среде отличается по модулю от индукции   магнитного поля в вакууме, называется магнитной проницаемостью: 

Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10^–5, у хлористого железа (FeCl₃) μ – 1 ≈ 2,5·10^–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10^–6), вода (μ – 1 ≈ –9·10^–6), висмут (μ – 1 ≈ –1,7·10^–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному –

Если собственный магнитный момент атомов отличен от нуля, вещество оказывается парамагнитным. Магнитное поле стремится установить магнитные моменты атомов вдоль  , а тепловое движение стремится разориентировать их равномерно по всем направлениям. В результате устанавливается некоторая преимущественная ориентация моментов вдоль поля, тем большая, чем больше  , и тем меньшая, чем выше температура.  С точки зрения макроскопической теории парамагнетики – это вещества, для которых   (как и у диамагнетиков) невелика, но положительна, а  несколько больше единицы: ,  . Парамагнетиками являются Na, K, Rb, Cs, Mg, Al, Мn, Рt, О, растворы солей железа и др. Восприимчивость парамагнетиков при обычных температурах лежит в пределах от 10^–3 до 10^–6. Так у алюминия  =2·10^-5, у платины  = 3·10^–4.  Кюри экспериментально установил закон, согласно которому магнитная восприимчивость парамагнитного вещества   (4.9) где С – постоянная Кюри, зависящая от рода вещества. Закон Кюри справедлив при не слишком низких температурах. Классическая теория парамагнетизма была развита П. Ланжевеном (Франция) в 1905 г.

22. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Переменный электрический ток.

Явление электромагнитной индукции (опыты Фарадея)

Эта фундаментальная задача была блестяще решена в 1831 г. английским физиком М. Фарадеем, открывшим явление электромагнитной индукции, заключается в том, что в замкнутом проводя­щем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

З начение индукционного тока совершенно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения

Открытие явления электромагнитной индукции имело большое значение, так как была доказана возможность получения электрического тока с помощью магнитного поля. Этим была установлена вза­имосвязь между электрическими и магнитными явлениями, что послужило в дальнейшем толчком для разработки теории электромагнитного поля.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.

Закон Фарадея может быть непосредственно получен из закона сохранения энергии, как это впервые сде­лал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно перемещаться. Под действием силы Ампера F, проводник перемещается на отрезок dx. Таким образом, сила Ампера производит работу dA=IdФ, где dФ — пересеченный проводни­ком магнитный поток.

Е сли полное сопротивление контура равно R, то, согласно закону сохранения энергии, работа источника тока за время dt (ξIdt) будет складываться из работы на джоулеву теплоту (I²Rdt) и работы по перемещению проводника в магнитном поле (IdФ):

откуда

где-dФ/dt=ξ_i есть не что иное, как закон Фарадея (см. (123.2)).

Закон Фарадея:э.д.с. ξ_i электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э.д.с. ξ_i не зависит от способа изменения магнитного потока.

Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

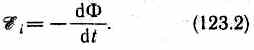
Какова природа э.д.с. электромагнитной индукции? Если проводник движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противо­положно току, т. е. она будет создавать в проводнике индукционный ток противоположного направления (за направление электрического тока принимается движение положительных зарядов). Таким образом, возбуждение э.д.с. индукции при движении контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении про­водника.

Согласно закону Фарадея, возникновение э.д.с. электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на непод­вижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция векто­ра Е_В этого поля по любому неподвижному контуру L проводника представляет собой э.д.с. электромагнитной индукции:

Переменный электрический ток

Переменный ток. Обозначение (~).

Электрический ток называется переменным, если он в течение времени меняет свое направление и непрерывно изменяется по величине.

Переменный ток, который используется для подключения бытовых или производственных электрических приборов, изменяется по синусоидальному закону:

i = I_msin(2πft)

i – мгновенное значение тока

Im – амплитудное или наибольшее значение тока

f – значение частоты переменного тока

t – время

Широко используется переменный ток благодаря тому, что электроэнергия переменного тока технически просто и экономно может быть преобразована из энергии более низкого напряжения в энергию более высокого напряжения и наоборот. Это свойство переменного тока позволяет передавать электроэнергию по проводам на большие расстояния.

Промышленный переменный электрический ток получают при помощи электрических генераторов, принцип работы которых основан на законе электромагнитной индукции. Вращение генератора осуществляется механическим двигателем, использующим тепловую, гидравлическую или атомную энергию.

Переменный однофазный электрический ток имеет следующие основные характеристики:

f – частота переменного тока определяет количество циклов или периодов в единицу времени. За единицу измерения частоты переменного тока принят Герц (Гц):

1гц = 10³кгц = 10⁶мгц

Τ – период – время одного полного изменения переменной величины.

Если в 1 секунду происходит 1 период Τ, то частота f = 1 Гц (Герц).

1c = 10³мс = 10⁶мкс = 10¹²нс

В Российской Федерации период Τпеременного тока принят равным 0,02секунды,следовательно по формуле f = 1/Τ можно определить частоту переменного тока:

f = 1/0,02 = 50 Гц

ω – угловая скорость

Помимо частоты f при изучении цепей переменного тока вводится понятие угловой скорости ω. Угловая скорость ω связана с частотой f следующим соотношением:

ω=2πf

При частоте 50 Гц угловая скорость равна 314 рад/с (2 × 3,14 × 50 = 314).

Мгновенное значение (i,u,e,p) – значение величины в данный момент, мгновенное.

Максимальное или амплитудное значение (Im,Um,Em,Pm).

Эффективное значение тока – это величина переменного тока, равная такому току, который на сопротивлении R, создаёт тепловыделение равное данному переменному току, за тоже время t(I,U,E,P).

I =

Im √2

U =

Um √2

23. Сопротивление, индуктивность и емкость в цепи переменного тока. Закон Ома для цепи переменного тока.

Закон Ома для переменного тока — Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается

  

Полное сопротивление :    

Сила переменного тока определяется при заданном напряжении не только сопротивлением R, которым обладает данная цепь при постоянном токе, но и наличием в этой цепи конденсаторов или катушек индуктивности. Поэтому, величины R и Z различны, т. е. одна и та же цепь будет иметь различное сопротивление для постоянного и для переменного тока.

В Формуле мы использовали :

 — Напряжение (разность потенциалов)

 — Сила тока

 — Полное сопротивление

 — Реактивное сопротивление

 — Активное сопротивление

24. колебательный контур. Затухающие электромагнитные колебания.

Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Резонансная частота контура определяется так называемой формулой Томсона:

Пусть конденсатор ёмкостью C заряжен до напряжения  . Энергия, запасённая в конденсаторе составляет

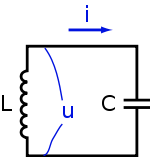
При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток  , что вызовет в катушке электродвижущую силу (ЭДС)самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.

Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора  . Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна

, где   — индуктивность катушки,   — максимальное значение тока.

После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения  .

В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.

В общем, описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.

Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.

Напряжение, возникающее в катушке при изменении протекающего тока равно

Аналогично для тока, вызванного изменением напряжения на конденсаторе:

Поскольку всё возникающее в катушке напряжение падает на конденсаторе, то  , а ток, вызванный конденсатором проходит через катушку, то  .Дифференцируя одно из уравнений и подставляя результат в другое, получаем

Это уравнение гармонического осциллятора с циклической частотой   (иначе она называется собственной частотой гармонического осциллятора)

Решением такого уравнения является

где   — некая постоянная, называемая амплитудой колебаний,   — также некоторая постоянная, называемая начальной фазой. И, например, при начальных условиях   решение сведётся к

Свободные затухающие колебания в электрическом колебательном контуре.

Дифференциальное уравнение свободных затухающих колебаний заряда в контуре (при R0) имеет вид (143.2))

Учитывая выражение (142.2) и принимая коэффициент затухания =R/(2L), (146.11) дифференциальное уравнение (143.2) можно записать в идентичном уравнению (146.1) виде

Из выражений (146.1) и (146.5) вытекает, что колебания заряда совершаются по закону Q=Q_me^-tcos((t+) (146.12) с частотой, согласно (146.4),

меньшей собственной частоты контура ₀ (см. (143.4)). При R=0 формула (146.13) переходит в (143.4).

Логарифмический декремент затуха­ния определяется формулой (146.7), а до­бротность колебательного контура (см. (146.8))

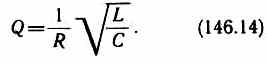
В заключение отметим, что при увели­чении коэффициента затухания  период затухающих колебаний растет и при =₀ обращается в бесконечность, т. е. движе­ние перестает быть периодическим. В дан­ном случае колеблющаяся величина асим­птотически приближается к нулю, когда t. Процесс не будет колебательным. Он называется апериодическим.

25. Вынужденные электромагнитные колебания. Резонанс.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющегося по гармоническому закону:

X(t)=X₀cost.

Если рассматривать электрический ко­лебательный контур, то роль X(t) играет подводимая к контуру внешняя периодиче­ски изменяющаяся по гармоническому за­кону э.д.с. или переменное напряжение

U=U_mcost. (147.3) Тогда уравнение (143.2) с учетом (147.3) можно записать в виде

Используя (143.4) и (146.11), придем к уравнению

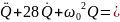
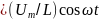(147.4)

Колебания, возникающие под действи­ем внешней периодически изменяющейся силы или внешней периодически изменя­ющейся э.д.с., называются соответствен­но вы­нужденными электромагнитными колеба­ниями.

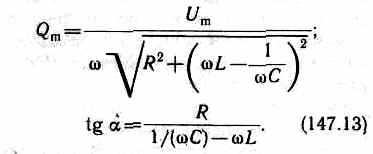
Продифференцировав Q=Q_mcos(t-) по t, найдем силу тока в контуре при установившихся колебаниях:

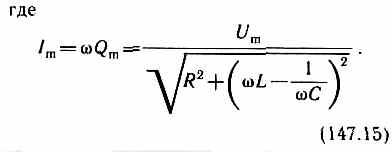
Выражение (147.14) может быть записано в виде I=I_mcos(t-), где =-/2 — сдвиг по фазе между током и приложенным напряжением (см. (147.3)). В соответствии с выражени­ем (147.13)

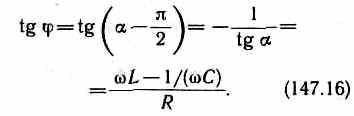
Из формулы (147.16) вытекает, что ток отстает по фазе от напряжения (>0), если L>l/(C), и опережает напряже­ние (<0), если L<l/(C).

Р езона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описаноГалилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

,

где   ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.