1.Электрические заряды и их взаимодействие. Закон кулона. Электрическое поле. Напряжённость поля. Силовые линии электростатического поля. Принцип суперпозиции электростати ческих полей.

Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Имеются 2 вида электрических зарядов, условно называемых положительными и отрицательными. Заряды одного знака отталкиваются, заряды разных знаков притягиваются. Электрический заряд является свойством некоторых элементарных частиц, например электрон имеет отрицательный заряд –e, протон – положительный заряд +e, нейтрон – заряд равный нулю. Заряд элементарных частиц одинаковый по величине и называется элементарным зарядом. Электрические заряды входят в состав атомов и молекул любого вещества. Обычно частицы, несущие отрицательный и положительный заряды присутствуют в веществе в одинаковом количестве (молекула нейтральна). Если создать избыток положительно заряженных частиц в теле, то тело станет положительно заряженным (положительно заряженный ион), и наоборот, если отрицательно заряженных частиц больше, то будем иметь отрицательно заряженное тело ( отрицательный ион).

В 1785 году Кулон экспериментально установил закон взаимодействия точечных зарядов. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд. Кулон с помощью крутильных весов измерял силу взаимодействия двух заряженных шариков в зависимости от величины зарядов на них и от расстояния между ними. Закон: Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с направлением прямой соединяющей заряды.

. k – коэффициент пропорциональности, предполагается положительным, 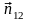- единичный вектор, имеющий направление от одного заряда к другому. Если имеется система зарядов : заряд q_a и еще n зарядов, то равнодействующая сила с которой действует заряд q_a определяется формулой - сила с которой действует на заряд q_a заряд q_i в отсутствие остальных n-1 зарядов. Таким образом можно вычислить силу взаимодействия между зарядами сосредоточенными на телах конечных размеров, для этого надо разбить каждый из зарядов на малые заряды, которые можно считать точенными, найти силу взаимодействия между всеми точенными зарядами взятыми попарно и найти векторную сумму этих сил.

В системе единиц СГСЭ ( абсолютная электростатическая система единиц: грамм, см, секунда, для заряда – СГСЭ абсолютная электростатическая единица заряда k=1 и закон кулона имеет вид .В системе СИ заряд измеряется в Кулонах опытным путем установили, что 1Кл =2.998 * 10⁹ единиц заряда СГСЭ. Элементарный заряд выраженный в Кулонах равен e= 1.60* 10^-19Кл.

В системе единиц СИ коэффициент пропорциональности в законе Кулона равен - электростатическая постоянная = 0.885 *10^-11Ф/м (Фарада/метр).

Напряженность электростатического поля

Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляется в том, что помещенный в какую-либо его точку электрический заряд испытывает воздействие силы. Взаимодействие между зарядами осуществляется через электрическое поле. Будем вносить пробные заряды в поле неподвижного точечного заряда и измеряя силы, действующие на пробный заряд было установлено, что отношение для всех пробных зарядов остается постоянным и зависит только от q и r, определяющих поле в данной точке.

Величину , характеризующую электрическое поле называют напряженностью электрического поля в данной точке пространства.

Направление вектора напряженности E – вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.

Электрическое поле можно описывать, указав для каждой точки величину и направление вектора E. Электрическое поле можно описать с помощью линий напряженности электрического поля. Линии напряженности проводят таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора E. Густота линий выбирается таким образом, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям площадки, была равна числовому значению вектора E. Тогда по картине линий вектора E можно судить о величине и направлении напряженности в разных точках пространства.

Принцип суперпозиции электрических полей.

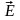На всякий точечный заряд q в точке поля с напряженностью E будет действовать сила . В случае отрицательного q направления векторов и совпадают. В случае отрицательного q направления векторов и противоположны. Так как сила с которой система зарядов действует на заряд не входящий в эту систему зарядов, равна векторной сумме сил, с которыми действуют на данный заряд каждый из зарядов системы в отдельности, вытекает принцип суперпозиции (наложения) электрических полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создал бы каждый из зарядов в отдельности .

Напряженность электрического поля от нескольких зарядов находится по правилу векторного сложения полей.Принцип суперпозиции позволяет вычислять напряженность поля любой системы зарядов. Разбив протяженные заряды на достаточно малые доли, любую систему можно свести к совокупности точечных зарядов.

2. Поток вектора напряжённости электростатического поля. Теорема Остроградского-Гаусса. Применение теоремы Остроградского-Гаусса для расчета поля, равномерно заряженной бесконечной плоскости.

Поток вектора напряженности электрического поля

Поток вектора.

Величина - поток вектора через поверхность. Поток вектора – это алгебраическая величина, знак которой зависит от выбора направления нормали к элементарной площадке, на которые разбивается поверхность S.

В случае замкнутых поверхностей принято вычислять поток «вытекающий» наружу, следовательно нормаль всегда подразумевается направленная наружу (внешняя нормаль).

Дивергенцией называется величина . Интеграл берется по произвольной замкнутой поверхности S, окружающей точку , V – объем ограниченный этой поверхностью. Так как поток через замкнутую поверхность определяется по формуле 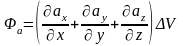, то разделив это выражение на , найдем дивергенцию вектора a в точке P .

Теорема Остроградского-Гаусса

Зная дивергенцию вектора в каждой точке пространства, можно вычислить поток этого вектора через любую замкнутую поверхность конечных размеров. Соотношение называется теоремой Остроградского-Гаусса. Интеграл в левой части вычисляется по произвольной замкнутой поверхности, в правой части – по объему, ограниченному этой поверхностью.

Силы, действующие на заряд q являются консервативными, т.е. работа этих сил на любом замкнутом контуре равна нулю:

. Сократив на q получим соотношение. Интеграл, стоящий в левой части представляет собой циркуляцию вектора по контуру Г. Т.о. циркуляция вектора напряженности по любому замкнутому контуру равна нулю.

Теорема Гаусса

Поток вектора E равен . Знак потока совпадает со знаком заряда. Допустим, что внутри замкнутой поверхности находится n точечных зарядов. В силу принципа суперпозиции напряженность E, создаваемая всеми зарядами, равна сумме напряженностей, создаваемых каждым зарядом в отдельности. Поэтому

- теорема Гаусса: ток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, делен на . При рассмотрении полей, создаваемых макроскопическими зарядами, отвлекаются от дискретной структуры этих зарядов и считают их распределенными в пространстве непрерывным образом с конечной всюду плотностью. Объемная плотность заряда ρ определяется по формуле .

В данном случае физически малый объем должен быть мал, чтобы плотность была одинаковой, но и не слишком мал, чтобы не появилась дискретность заряда. Зная плотность заряда в каждой точке пространства, можно вычислить суммарный заряд

заменяя поверхностный интеграл объемным, получим . И следовательно дивергенция вектора напряженности связана с плотностью заряда в той же точке равенством . – теорема Гаусса в дифференциальной форме.

Теорема Гаусса позволяет вычислять напряженность полей. Поверхностная плотность определяется по формуле ( если заряд сосредоточен в тонком поверхностном слое), линейная плотность (если заряд равномерно распределен в каждом сечении).

Поле бесконечной заряженной плоскости.

Пусть поверхностная плотность заряда во всех точках одинакова и равна σ. Будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность поля в любой точке имеет направление перпендикулярное к плоскости.

Далее очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величие и противоположна по направлению. Пусть цилиндрическая поверхность с образующими перпендикулярными к плоскости и основаниями величины , расположенными относительно плоскости симметрично. Применим к поверхности теорему Гаусса. П через боковую поверхность равен нулю, т. к. в каждой точке поверхности равен нулю. Для из которого следует - напряженность поля бесконечной плоскости.

3. Работа по перемещению заряда в электростатическом поле. Потенциальный характер электростатического поля. Потенциал. Связь между напряженностью электростатического поля и потенциалом.

Работа по перемещению заряда в электростатическом поле

Рассмотрим поле, создаваемое неподвижным зарядом q. В любой точке этого поля на точечный заряд действует сила Кулона . Так как сила является центральной, поле этой силы консервативно. Следовательно, работа которая совершается силами поля над зарядом при перемещении из одной точки в другую не зависит от пути.

Работа равна , dl – элементарное перемещение. . - потенциальная энергия. Работа консервативного поля может быть представлена как убыль потенциальной энергии. .

и следовательно

Интеграл может быть взят по любой Линии, соединяющей точки 1 и 2. Для обхода по замкнутому контуру 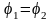, т.е. . Это соотношение справедливо только для электростатического поля.

Потенциальный характер электростатического поля. Потенциал.

Потенциал электростатического поля, разность потенциалов. Потенциал точечного заряда.

Рассмотрим поле, создаваемое неподвижным зарядом q. В любой точке этого поля на точечный заря действует сила Кулона . Так как сила является центральной, поле этой силы консервативно. Следовательно работа, которую совершается силами поля над зарядом при перемещении из одной точки в другую не зависит от пути.

Работа равна , dl – элементарное перемещение. . - потенциальная энергия. Работа консервативного поля может быть представлена как убыль потенциальной энергии. .

Будем вносить в поле разные пробные заряды. Разные пробные заряды будут обладать в одной и той же точке разными потенциальными энергиями.

Однако отношение потенциальной энергии к пробному заряду остается одинаковой для всех зарядов. Величина называется потенциалом поля в данной точке и является еще одной характеристикой поля наряду с напряженностью E. Из формулы следует, что потенциал численно равен . – потенциал поля точечного заряда. Потенциал системы n зарядов равен : равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

Заряд находящийся в точке поле с потенциалом φ обладает потенциальной энергией . Следовательно работа поля над зарядом q может быть выражена формулой . Таким образом, работа, совершаемая над зарядом полем равна произведению заряда на разность потенциалов в начальной и конечной точках. Если заряд q из точки с потенциалом φ удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна нулю .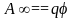

Следовательно, потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность. Единицы потенциала 1В = 1Дж/1Кл.

Связь между напряженностью поля и его потенциалом

, , , следовательно и .

Напряженность поля точечного заряда , а потенциал поля точечного заряда .

Связь между напряженностью электростатического поля и потенциалом.

Электрическое поле можно описать либо с помощью векторной величины напряженности электрического поля E, либо с помощью скалярной величины φ.

Сила связана с напряженностью , потенциальная энергия связана с потенциалом , сила связана с потенциальной энергией , следовательно, и .- это соотношение устанавливает связь между напряженностью и потенциалом. Т.о. По известным значениям потенциала можно найти значение напряженности поля. Можно решить и обратную задачу, по заданным значениям напряженности в каждой точке найти разность потенциала между двумя произвольными точками поля.

Это следует из формул для работы , также работа может быть вычислена по формуле 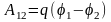. Приравнивая друг к другу эти выражения и сократив на q. Получим соотношение .

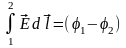4. Деление веществ на металлы, полупроводники и диэлектрики с точки зрения Зонной теории.

Основным вопросом при изучении электрических свойств твердых тел  является вопрос проводимости веществами электрического тока. Из зонной теории следует, что проводимость зависит от двух факторов:

• ширины запрещенных зон;

• различием заполнения электронами разрешенных энергетических зон.

Подобно тому, как в отдельном атоме электроны могут переходить с одного энергетического уровня на другой, электроны в кристаллах могут совершать переходы внутри одной и той же зоны, а так же переходить из одной разрешенной зоны в другую. Термин «переход» означает, что изменяется состояние электрона в кристалле. Для перехода электрона из нижней энергетической зоны в соседнюю верхнюю разрешенную зону необходимо:

• энергия, равная ширине запрещенной зоны, лежащей между ними;

• наличие свободного энергетического уровня в верхней зоне.

Зона, которая полностью заполнена электронами, называется валентной зоной, а зона, которая либо частично заполнена электронами, либо свободна, называется зоной проводимости (свободной зоной). Возможны разные  варианты положения энергетических зон относительно друг друга и их заполнения электронами, что приводит к разделению веществ на проводники, полупроводники и диэлектрики. Проводники.

• Если зона не полностью заполнена электронами, то твердое тело является проводником (рисунок 8.3.3.а.). Под действием электрического поля, создаваемого в кристалле источником тока, электроны в зоне проводимости увеличивают свою энергию за счет работы источника тока и переходят на более высокие энергетические уровни, возникает упорядоченное движение заряженных частиц или электрический ток. Типичные представители проводников с таким типом проводимости являются металлы первой группы периодической системы Менделеева.

• Твердое тело будет проводником также в том случае, если имеется перекрытие зон, и образуется гибридная зона, причем, нижняя часть этой зоны заполнена электронами, а верхняя пуста, но перекрывается нижней  (рисунок 8.3.3.б.). Щелочноземельные металлы относятся к таким проводникам.

Диэлектрики. В твердых диэлектриках энергетические зоны не перекрываются, и зона, объединяющая энергетические уровни валентных электронов, целиком заполнена электронами, а выше расположенная зона при Т → 0 К совершенно пуста. Ближайшая свободная зона расположена от заполненной зоны на расстоянии по энергии более 2   3 эВ (рисунок 8.3.3.в). В случае и полупроводников, и диэлектриков все энергетические состояния в валентной зоне заняты, переходы с одного уровня на другой запрещены принципом Паули, и внешнее электрическое поле не приводит к направленному движению электронов, т.е. к возникновению электрического тока. Полупроводники – твердые тела, имеющие полностью заполненные валентные зоны, так же как у диэлектрика, а ближайшая свободная зона, не занятая электронами, отстоит на расстоянии по энергии менее 2 эВ. Деление твердых тел на полупроводники и диэлектрики условно. Для перехода электрона из одной зоны в другую и преодоление запрещенной зоны необходима энергия, по величине не менее энергии запрещенной зоны. Эта энергия может быть получена твердым телом либо при нагревании последнего, либо при облучении его светом. Переход электрона «зона – зона» соответствует на самом деле в собственных (чистых) полупроводниках разрыву ковалентных связей. Появление носителей заряда в валентной зоне (дырки) или в свободной зоне (электронов) может происходить в примесных полупроводниках. Энергия, необходимая для таких процессов равна энергии активации примеси, которая по величине меньше энергии запрещенной зоны. Процессы активации примесей происходят при температурах, значительно ниже, чем процесс разрыва ковалентных связей.

Рисунок 8.3.3. – Энергетические диаграммы проводника (а, b), полупроводника (с), диэлектрика (d) при нормальных условиях. Обозначения, принятые на рисунке: система линий – энергетические уровни, точки – изображения электронов, находящихся на этих уровнях.

5. Проводники в электрическом поле. Электрический экран. Электрическая емкость конденсатора.

Носители заряда в проводнике способны перемещаться под действием сколь угодно малой силы. Поэтому для равновесия зарядов на проводнике необходимо выполнение следующих условий:

• напряженность поля всюду внутри проводника должна быть равна нулю ; (потенциал внутри проводника должен быть постоянным)

• напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности ..

Следовательно в случае равновесия зарядов поверхность проводника будет эквипотенциальной( поверхность все точки которой имеют одинаковый потенциал). Если проводящему телу сообщить заряд q, то он распределиться так, чтобы соблюдались условия равновесия. Пусть имеет произвольную замкнутую поверхность полностью заключенную внутри тела. При равновесии зарядов поле в каждой точке отсутствует, поэтому поток электрического смещения равен нулю

По теореме Гаусса сумма зарядов внутри поверхности тоже будет равна нулю. Следовательно при равновесии зарядов ни в каком месте проводника не может быть избытка зарядов, они распределяются равномерно по поверхности с некоторой плотностью σ.

Электрический экран.

Если внутри проводника имеется полость, то при равновесном распределении зарядов поле внутри проводника становится равным нулю . На этом основывается электростатическая защита. Когда какой-то прибор хотят защитить от воздействия внешнего поля, его окружают проводящим экраном.

Внешнее поле компенсируется внутри экрана возникающими на его поверхности индуцированными зарядами. Такой экран может быть и не сплошным, а сделанным из густой сетки.

Электрическая емкость конденсатора.

Устройства - которые при небольшом потенциале накапливают в себе(конденсируют) большие по величине заряды. Такие устройства называются конденсаторами и в их основу положен тот факт, что электроемкость проводников возрастает при приближении к ним других тел. Это вызвано тем, что под действием поля, создаваемого заряженным проводником, на поднесенном к нему теле возникают индуцированные заряды. Заряды противоположные по знаку заряду проводника q располагаются ближе к проводнику и оказывают влияние на проводник. А именно его потенциал уменьшается, а следовательно емкость возрастает.

Конденсаторы делают в виде двух проводников, помещенных близко друг к другу, образующие конденсатор проводники называются его обкладками. Чтобы внешние тела не оказывали влияние на емкость конденсатора, их делают такими (по форме и расположению друг относительно друга), чтобы поле, создаваемое зарядами было сосредоточено внутри конденсатора.

Это могут быть две пластинки, две концентрические сферы, два коаксиальных цилиндра. Следовательно, сущ. плоские, сферические и цилиндрические конденсаторы. Так как поле сосредоточено внутри конденсатора, линии напряженности начинаются на одной обкладке и заканчиваются на другой. И след. Сторонние заряды, возникающие на обкладках, имеют одинаковую величину и противоположны по знаку.

Основной характеристикой конденсатора является его емкость, под которой понимают величину, пропорциональную заряду и обратно пропорциональную разности потенциалов между обкладками .

Разность потенциалов называют напряжением между соответствующими точками и обозначают буквой U (напряжение между обкладками). Тогда можно переписать формулу . Емкость конденсаторов измеряется в тех же единицах, что и емкость уединенного проводника. Величина емкости зависит от геометрии конденсатора (форме, размеров, расстояния между обкладками), а также диэлетрическими свойствами среды, заполняющими пространство между обкладками.

6. Диэлектрики во внешнем электростатическом поле. Электронная поляризация.

При внесении диэлектрика во внешнее электрическое поле   в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.

Связанные заряды создают электрическое поле   которое внутри диэлектрика направлено противоположно вектору напряженности   внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле   внутри диэлектрика оказывается по модулю меньше внешнего поля 

Физическая величина, равная отношению модуля напряженности   внешнего электрического поля в вакууме к модулю напряженности   полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества. 

Электронный или упругий механизм проявляется при поляризации неполярных диэлектриков, молекулы которых не обладают в отсутствие внешнего поля дипольным моментом. Под действием электрического поля молекулы неполярных диэлектриков деформируются – положительные заряды смещаются в направлении вектора   а отрицательные – в противоположном направлении. В результате каждая молекула превращается в электрический диполь, ось которого направлена вдоль внешнего поля. На поверхности диэлектрика появляются нескомпенсированные связанные заряды, создающие свое поле   направленное навстречу внешнему полю   Так происходит поляризация неполярного диэлектрика (рис. 1.5.4).

Деформация неполярных молекул под действием внешнего электрического поля не зависит от их теплового движения, поэтому поляризация неполярного диэлектрика не зависит от температуры. Примером неполярной молекулы может служить молекула метана CH₄. У этой молекулы четырехкратно ионизированный ион углерода C^4– располагается в центре правильной пирамиды, в вершинах которой находятся ионы водорода H⁺. При наложении внешнего электрического поля ион углерода смещается из центра пирамиды, и у молекулы возникает дипольный момент,

п ропорциональный внешнему полю.

Рисунок 1.5.4.

Поляризация неполярного диэлектрика

7. Поляризация ионных диэлектриков.

Ионные диэлектрики

Ионные соединения представляют собой твердые неорганические диэлектрики с ионным типом химической связи. Для этой группы соединений характерны кроме электронной, ионная и электронно-релаксационная поляризации. Принято выделять группу диэлектриков с быстрыми видами поляризаций - электронной и ионной, и с замедленными видами поляризаций релаксационного типа, накладывающихся на электронную и ионную поляризации. К первой группе, в которой наблюдаются только быстрые виды поляризаций, относятся кристаллические вещества с плотной упаковкой ионов. К ним относятся каменная соль, кварц, слюда, корунд и др. Ко второй группе, в которой кристаллические диэлектрики с неплотной упаковкой ионов в решетке имеют также и ионно-релаксационную поляризацию, относятся неорганические стекла, электротехнический фарфор, ситаллы, микалекс и др.

Твердые диэлектрики ионного строения с плотной упаковкой решетки ионами:

Для диэлектриков этой группы (например, корунд, кварц, слюда) характерны электронная и ионная поляризации; диэлектрическая проницаемость от частоты приложенного напряжения не зависит, так как от частоты не зависят и . Значение изменяется в пределах от 3,2 до 10 и выше, у титаносодержащих кристаллов — до 173. При нагревании диэлектрическая проницаемость обычно возрастает (TKs положительный), так как возрастает (рис. 2.28, а).

У некоторых диэлектриков (титаносодержащая керамика) TKs отрицательный, поэтому при нагревании у них уменьшается.

Диэлектрики ионного строения аморфные и кристаллические с неплотной упаковкой решетки ионами:

Рис. 2.28. Температурная зависимость диэлектрика с плотной упаковкой решетки — корунда (а) и с не плотной упаковкой решетки — электротехнического фарфора (б). Образующие :1 — (Т) (T); 2 — (T); 3 — n (T); 4 — 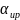(Т)

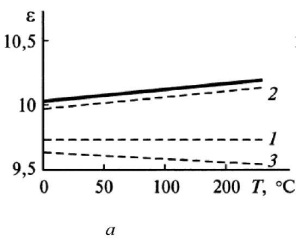Д иэлектрическая проницаемость таких диэлектриков (например, электротехнический фарфор, неорганические стекла, асбест) зависит от температуры и частоты напряжения вследствие проявления ионной и, главным образом, ионно- релаксационной поляризаций (см. рис. 2.28, б). Величина у них изменяется в пределах примерно от 4 до 20 и выше, т. е. мало отличается от диэлектриков с плотной упаковкой решетки. У этих диэлектриков ТК положительный и в отличие от TK диэлектриков ионного строения с плотной упаковкой решетки имеет высокие значения. Увеличение диэлектрической проницаемости при нагревании происходит преимущественно за счет роста концентрации ионов, принимающих участие в ионно-релаксационной поляризации. Зависимость диэлектрической проницаемости от частоты напряжения примерно такая же, как у диэлектриков молекулярного строения полярных (см. рис. 2.25, а). При низких частотах в формировании принимают участие три вида поляризации: электронная, ионная и ионно-релаксационная. При высоких частотах (при ~10⁶—Ю¹⁰ Гц и выше) из-за малого времени полупериода напряжения становится исчезающе малой, поэтому

величину определяют только поляризуемости и _и. С увеличением размера иона и его валентности наибольшая частота напряжения, при которой проявляется а понижается.

8, Ориентационная поляризация

Ориентационная поляризация наблюдается у полярных диэлектриков. Внешнее электрическое поле стремится ориентировать дипольные моменты полярных молекул жестких диполей по направлению вектора напряженности поля. Этому препятствует хаотическое тепловое движение молекул, вызывающее беспорядочный разброс диполей. В итоге совместного действия поля и теплового движения возникает преимущественная ориентация дипольных электрических моментов вдоль поля, возрастающая с увеличением напряженности электрического поля и с уменьшением температуры.

Ориентационная поляризация имеет место в диэлектрике, молекулы которого обладают собственным электрическим моментом с хаотической ориентацией их в отсутствие внешнего электрического поля. Такие молекулы называют полярными; под действием внешнего поля Е они ориентируются в соответствующем направлении.

Ориентационная поляризация имеет место в газах и жидкостях, где молекулы достаточно подвижны. В твердых телах ( кристаллах) свобода движения частиц настолько ограничена, что ориентацион-ной поляризацией практически можно пренебречь.

Ориентационная поляризация характерна лишь для полярных диэлектриков ( полимеров); она существенно зависит от температуры. Диполи - полярные группы, имеющиеся в полимерах, могут при этом лишь упруго колебаться при воздействии электрического поля. С увеличением температуры диполи приобретают энергию, достаточную для преодоления внутримолекулярного взаимодействия; при этом осуществляется более полная ориентация в направлении приложенного поля. Вследствие этого поляризация резко возрастает, что вызывает рост диэлектрической проницаемости.

9. Постоянный электрический ток. Условие существования электрического тока. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной форме. Работа и мощность тока. Закон

Всякое упорядоченное движение заряженных частиц называется электрическим током. За направление тока условно принимают направление движения положительных зарядов. Электрический ток, проходящий через данную поверхность, характеризуется силой тока I.

Сила тока есть скалярная величина, численно равная заряду dq, который переноситься через площадку S в единицу времени, т.е.

(17.1)

Если за любые равные промежутки времени через любое сечение проводника проходят одинаковые количества электричества и направление движения зарядов не изменяется, то такой ток называется постоянным и тогда I=q/t. В системе СИ единица тока является основной и носит название - Ампер.

Условие существования электрического тока.

1. наличие свободных носителей зарядов,

2. наличие разности потенциалов;

3. замкнутая цепь,

4. источник сторонних сил, который поддерживает разность потенциалов.

Закон Ома в дифференциальной форме.

Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике: (17.5)

Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении 1В течет ток в 1 А.

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан

Закон Ома можно записать в дифференциальной форме. Выделим в проводнике элементарный цилиндрический объем dV с образующими, dl параллельными вектору плотности тока в данной точке (рис. 17.2). Через поперечное сечение dS цилиндра течет ток силой . Напряжение, приложенное к цилиндру, равно , где Е - напряженность поля в данном месте. Сопротивление цилиндра . Подставив эти значения в уравнение (17.5), получим

Носители заряда в каждой точке движутся в направлении вектора . Поэтому направления векторов и совпадают. Таким образом, можно написать

Эта формула выражает закон Ома в дифференциальной форме.

Закон Джоуля-Ленца в дифференциальной и интегральной форме.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов , тогда работу по переносу заряда q на этом участке равна

По определению I= q/t. откуда q= I t

Следовательно

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

-----Закон Джоуля – Ленца в интегральной форме. (17.13)

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме.

Введем плотность тепловой мощности , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

где S - поперечное сечение проводника, - его длина.

Используя (1.13) и соотношение , получим

Но - плотность тока, а , тогда

с учетом закона Ома в дифференциальной форме , окончательно получаем

(17.14)

Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Работа и мощность тока.

Формулировка:  Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.  Формула:  A= U*I*t  1 Джоуль = 1 Вольт * 1 Ампер * 1 секунда  ______  Формулировка:  Мощность электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока.  Формула:  P=UI  1 Ватт = 1 Вольт * 1 Ампер

10. Правила Кирхгофа и их физический смысл. Применение правил Кирхгофа для расчета раз- ветвленных цепей.

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.

В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.

Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3,I4 < 0

В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:

Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

I1 + I2 + I3 + ... + In = 0.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.

В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).

Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef)

В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.

Второе правило Кирхгофа является следствием обобщенного закона Ома.

Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.

Рисунок 1.10.3. «Правила знаков»

Для участков контура abcd обобщенный закон Ома записывается в виде:

Для участка bc: I₁R₁ = Δφ_bc –  ₁.

Для участка da: I₂R₂ = Δφ_da –  ₂.

Складывая левые и правые части этих равенств и принимая во внимание, что Δφ_bc = – Δφ_da , получим: 

I1R1 + I2R2 = Δφbc + Δφda –  1 +  2 = – 1 –  2.

Аналогично, для контура adef можно записать: 

– I2R2 + I3R3 =  2 +  3.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I₁, I₂ и I₃ имеет вид: 

I1R1 + I2R2 = –  1 –  2,

– I2R2 + I3R3 =  2 +  3,

– I1 + I2 + I3 = 0.

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.

11. Электрический ток в металлах и полупроводниках. Температурная зависимость сопротивле- ния в металлах и полупроводниках.

Электрический ток есть направленное движение заряженных частиц - свободных носителей заряда. Без внешнего электрического поля эти носители совершают беспорядочное тепловое движение.

Средний модуль скорости теплового движения электронов при комнатных температурах порядка 10⁵ м/с. Внешнее электрическое поле действует на носитель заряда силой

F=qE, (7.1)

где Е – напряженность поля, q – заряд носителя. Таким образом, внешнее поле создает направленное движение носителей заряда – электрический ток с плотностью тока

j=nqu. (7.2)

Здесь n – коцентрация носителей заряда, u – направленная (дрейфовая) скорость носителей. Если ток практически создается одним типом носителей (например, электронами), формула (7.2) дает полную плотность тока в исследуемом образце.

В кристаллах (и еще в ряде сред) носители заряда претерпевают частые столкновения с другими частицами. Это ведет к двум важным следствиям: дрейфовая скорость носителей много меньше средней скорости их теплового движения (u << v) и пропорциональна силе F, а, следовательно, и напряженности поля

U = μE. (7.3)

Величину μ называют подвижностью носителей заряда. Пропорциональной напряженности поля оказывается и плотность тока. Из (7.2) и (7.3) следует

j = σE, (7.4)

где σ = qnμ (7.5)

есть параметр конкретного материала – его удельная проводимость. Обратную величину ρ = 1 / σ – называют удельным сопротивлением. Соотношение (7.4) представляет собой дифференциальную (векторную) форму закона Ома.

Зависимость проводимости от температуры существенно различна для металлов и полупроводников.

В металлах практически все валентные электроны свободны. Поэтому температура не может заметно изменить концентрации свободных носителей n; изменение проводимости определяется температурной зависимостью подвижности электронов σ ~ μ.

Подвижность же тем больше, чем реже столкновения носителей со всякого рода дефектами кристаллической решетки. Таковыми являются атомы примеси, отклонения от идеального регулярного расположения атомов в узлах решетки за счет, например, тепловых колебаний и пр. Увеличение с ростом температуры интенсивности тепловых колебаний атомов и беспорядочной скорости электронов увеличивает частоту столкновений между ними. Это ведет к уменьшению подвижности носителей заряда.

Сопротивление металлов возрастает с увеличением температуры по закону

, (7.6)

где R_о – сопротивление металла при Т = 0 ^оС, ,  – коэффициенты. Обычно всеми коэффициентами, кроме , пренебрегают из-за их малости и считают R линейно зависимой от температуры

. (7.7)

 называют температурным коэффициентом сопротивления. Его можно вычислить, измерив зависимость сопротивления от температуры и продифференцировав полученный график (рис.7.1). Тогда

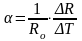, (7.8)

где R / T – тангенс угла наклона прямой к точке t. За R_о можно принять сопротивление при Т = 20 ^оС.

В полупроводнике валентные электроны связаны с ядрами атомов значительно сильнее, чем в металле. «Оторваться» от атома и превратиться в электрон проводимости могут лишь те из них, которые обладают избыточной энергией, не меньшей некоторого ε. ε называют шириной запрещенной зоны.

Рис. 7.1

В чистом собственном полупроводнике, разрыв каждой связи приводит к образованию пары электрон-дырка (разорванная межатомная связь).

Дырки перемешаются в направлении внешнего электрического поля, т.е. являются свободными носителями положительного элементарного заряда. Плотность тока в полупроводнике слагается из плотности тока электронов j_- и плотности тока дырок j₊. Следовательно, удельная проводимость (см. формулу (7.5))

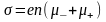, (7.9)

так как в собственном полупроводнике концентрации электронов и дырок одинаковы (n₊ = n_– = n), а подвижности μ_– и μ ₊ различны. Но μ_– и μ ₊ зависят от температуры много слабее, чем концентрация носителей заряда n каждого знака. Поэтому для полупроводника можно приближенно считать σ ~ n.

Разрыв связей (генерация свободных носителей) достигается за счет энергии тепловых колебаний атомов. Среднее её значение порядка kТ (где k – постоянная Больцмана; при комнатной температуре kТ  4·10^-21 Дж  2.5·10^-2 эВ). Процесс генерации носителей сопровождается обратным процессом рекомбинации электронов проводимости с дырками. Равновесие наступает, когда средняя частота актов рекомбинации равна средней частоте актов генерации. Расчет дает, что равновесная концентрация свободных носителей при этом

. (7.10)

Следовательно, удельная проводимость полупроводника зависит от температуры следующим образом

, (7.11)

а удельное сопротивление

. (7.12)

Из формулы (7.12) видно, что с увеличением температуры сопротивление полупроводников уменьшается (рис. 7.1).

(7.13)

Энергию активации ε можно вычислить, прологарифмировав выражение (7.13).

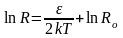
Это приводит к линейной зависимости lnR от 1 / Т. Поэтому, построив график lnR = f (1 / T), можно определить энергию активации.

(7.14).

Тогда ε = 2ktg.