1.2.Ранжированный ряд в порядке возрастания значения признака
|
№ п/п |
авт/ч |
№ п/п |
авт/ч |
№ п/п |
авт/ч |
№ п/п |
авт/ч |
|
1 |
2 |
26 |
5 |
51 |
8 |
76 |
10 |
|
2 |
2 |
27 |
5 |
52 |
8 |
77 |
10 |
|
3 |
2 |
28 |
5 |
53 |
9 |
78 |
10 |
|
4 |
2 |
29 |
5 |
54 |
9 |
79 |
10 |
|
5 |
2 |
30 |
5 |
55 |
9 |
80 |
11 |
|
6 |
3 |
31 |
5 |
56 |
9 |
81 |
11 |
|
7 |
3 |
32 |
6 |
57 |
9 |
82 |
11 |
|
8 |
3 |
33 |
6 |
58 |
9 |
83 |
11 |
|
9 |
3 |
34 |
6 |
59 |
9 |
84 |
12 |
|
10 |
3 |
35 |
6 |
60 |
9 |
85 |
13 |
|
11 |
3 |
36 |
6 |
61 |
9 |
86 |
13 |
|
12 |
3 |
37 |
6 |
62 |
9 |
87 |
13 |
|
13 |
3 |
38 |
7 |
63 |
9 |
88 |
14 |
|
14 |
4 |
39 |
7 |
64 |
10 |
89 |
14 |
|
15 |
4 |
40 |
7 |
65 |
10 |
90 |
16 |
|
16 |
4 |
41 |
7 |
66 |
10 |
91 |
16 |
|
17 |
4 |
42 |
7 |
67 |
10 |
92 |
18 |
|
18 |
4 |
43 |
7 |
68 |
10 |
93 |
19 |
|
19 |
4 |
44 |
7 |
69 |
10 |
94 |
21 |
|
20 |
4 |
45 |
7 |
70 |
10 |
95 |
21 |
|
21 |
4 |
46 |
8 |
71 |
10 |
96 |
22 |
|
22 |
4 |
47 |
8 |
72 |
10 |
97 |
26 |
|
23 |
5 |
48 |
8 |
73 |
10 |
98 |
28 |
|
24 |
5 |
49 |
8 |
74 |
10 |
99 |
31 |
|
25 |
5 |
50 |
8 |
75 |
10 |
100 |
35 |
1.3. Дискретный вариационный ряд
|
х, авт/ч |
f |
|
2 |
5 |
|
3 |
8 |
|
4 |
9 |
|
5 |
9 |
|
6 |
6 |
|
7 |
8 |
|
8 |
7 |
|
9 |
11 |
|
10 |
16 |
|
11 |
4 |
|
12 |
1 |
|
13 |
3 |
|
14 |
2 |
|
16 |
2 |
|
18 |
1 |
|
19 |
1 |
|
21 |
2 |
|
22 |
1 |
|
26 |
1 |
|
28 |
1 |
|
31 |
1 |
|
35 |
1 |
|
Итого |
100 |
1.4. Построить интервальный вариационный ряд, подобрав наилучшее число интервалов.
i=(35-2/)6=5,5
|
Интервал |
f |
Хц |
Σf |
|
2 - 7,50 |
45 |
4,75 |
45 |
|
7,5 - 13,00 |
42 |
10,25 |
87 |
|
13,00 - 18,50 |
5 |
15,75 |
92 |
|
18,50 - 24,00 |
4 |
21,25 |
96 |
|
24,00 - 29,50 |
2 |
26,75 |
98 |
|
29,50 - 35,00 |
2 |
32,25 |
100 |
|
Итого |
100 |
|
|
i=(35-2)/7=4.71
|
Интервал |
f |
Хц |
Σf | |||
|
2 - 6,71 |
37 |
4,4 |
37 | |||
|
6,71 - 11,42 |
46 |
9,07 |
83 | |||
|
11,42 - 16,12 |
8 |
13,77 |
91 | |||
|
16,12 - 20,83 |
2 |
18,48 |
93 | |||
|
20,83 - 25,54 |
3 |
23,19 |
96 | |||
|
25,54 - 30,25 |
2 |
27,90 |
98 | |||
|
30,25 - 35,00 |
2 |
32,63 |
100 | |||
|
Итого |
100 |
|
| |||
i=(35-2)/8=4,13
|
Интервал |
f |
Хц |
Σf | |||
|
2 - 6,13 |
37 |
4,07 |
37 | |||
|
6,13 - 10,26 |
42 |
8,20 |
79 | |||
|
10,26 - 14,39 |
10 |
12,33 |
89 | |||
|
14,39 - 18,52 |
3 |
16,46 |
92 | |||
|
18,52 - 22,65 |
4 |
20,59 |
96 | |||
|
22,65 - 26,78 |
1 |
24,72 |
97 | |||
|
26,78 - 30,91 |
1 |
28,85 |
98 | |||
|
30,91 -35,00 |
2 |
32,96 |
100 | |||
|
Итого |
100 |
|
| |||
1.5. Для каждого из полученных рядов вычислить: среднюю арифметическую; моду; медиану; показатели вариации (размах вариации, среднее линейное и среднее квадратическое отклонение, дисперсию, коэффициент вариации).
Среднеарифметическая взвешенная.
Дискретный вариационный ряд.
,
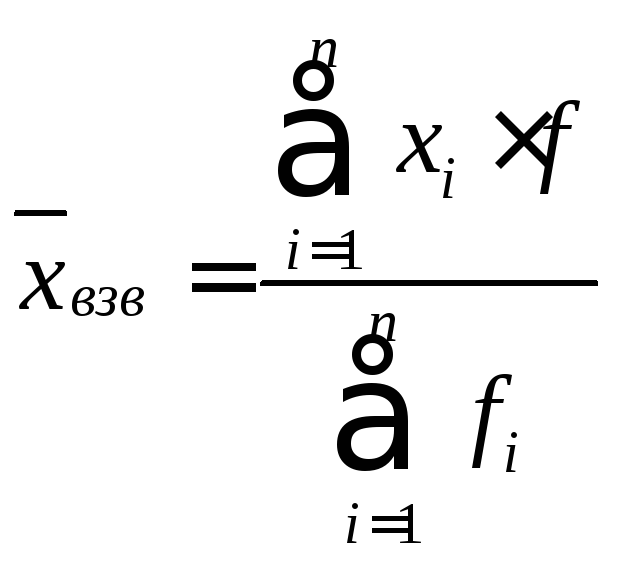где
Σxi∙fi – сумма произведений значений признака и их частот;
Σfi – сумма всех частот.
Интервальный вариационный ряд.
,
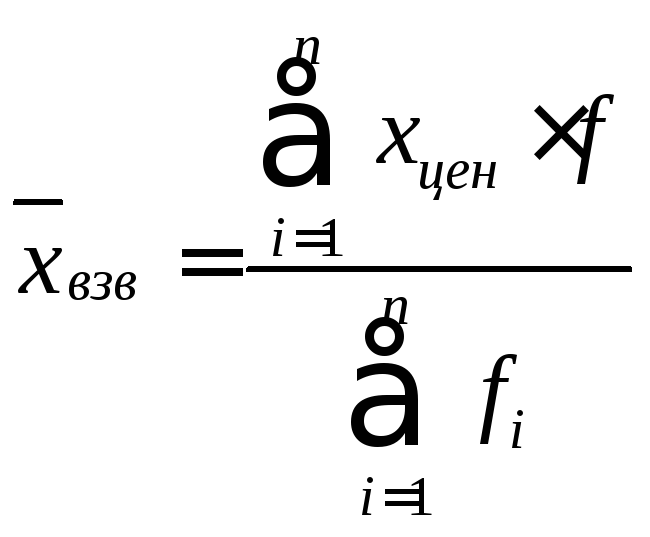где
Σxцен∙fi – сумма произведений центров интервалов и их частот;
Σfi – сумма всех частот.
Мода.
Дискретный вариационный ряд.
Это вариант имеющий наибольшую частоту f.
Интервальный вариационный ряд.
,
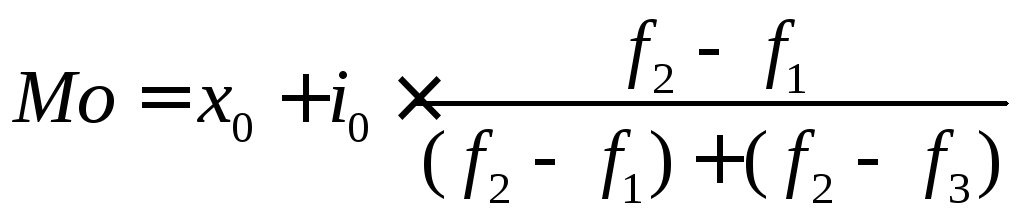где
х0 – нижняя граница модального интервала;
i0 – величина модального интервала;
f1, f2, f3 – частота интервала предшествующего, модального и следующего за модальным.
Медиана.
Дискретный вариационный ряд.
Это вариант стоящий в центре ранжированного ряда.
Интервальный вариационный ряд.
,
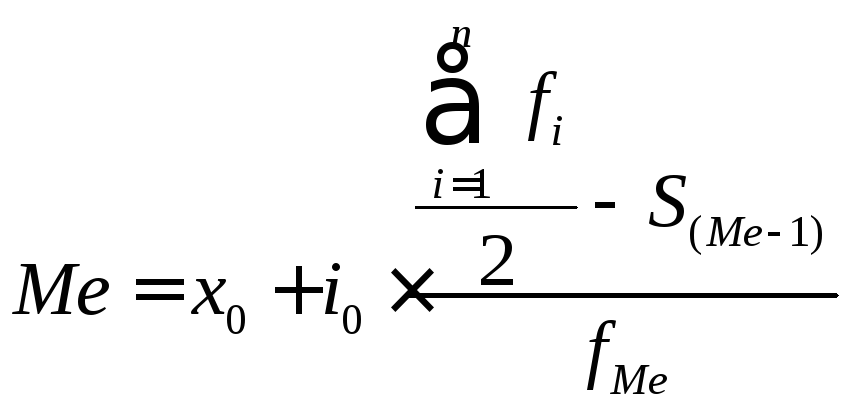где
х0 – нижняя граница медианного интервала;
i0 – величина медианного интервала;
Σfi – сумма всех частот;
S(Me – 1) – сумма накопленных частот интервалов, предшествующих медианному;
fMe – частота медианного интервала.
Размах вариации.
Среднее линейное отклонение.
Дискретный вариационный ряд.
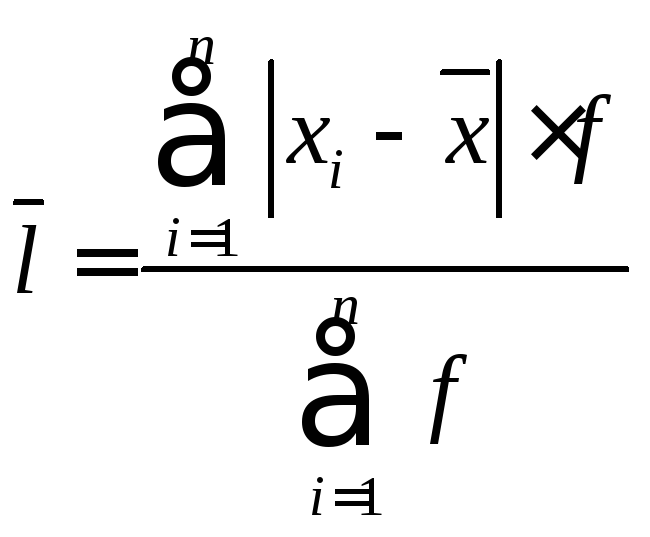
Интервальный вариационный ряд.
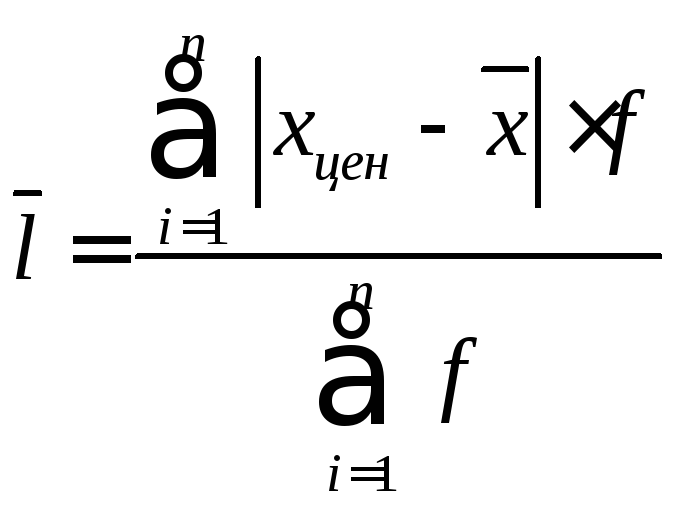
Дисперсия (средняя квадратов отклонений).
Дискретный вариационный ряд.
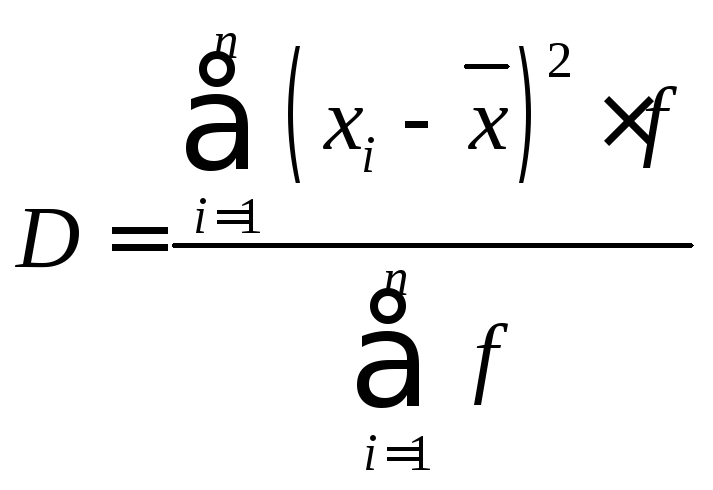
Интервальный вариационный ряд.
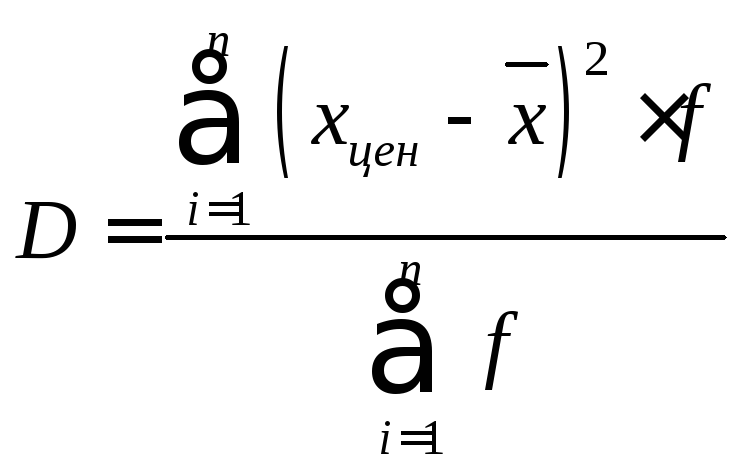
Среднее квадратическое отклонение.
Коэффициент вариации.
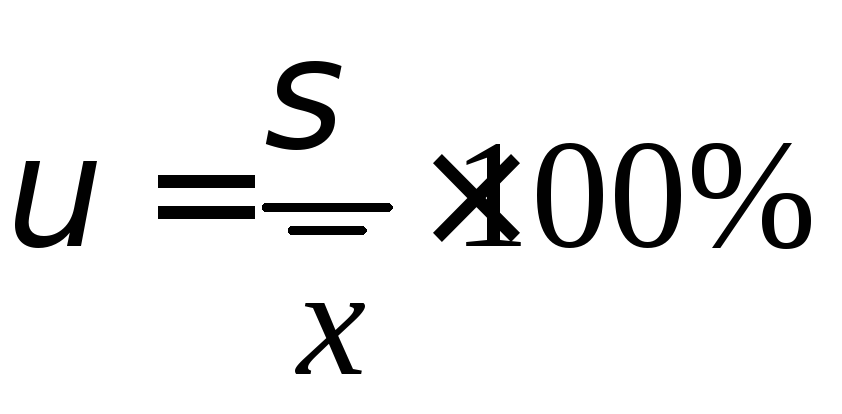
1.5.1 Для интервального вариационного ряда.
Х=(45*4,75+42*10,25+5*15,75+4*21,25+2*26,75+2*32,25)/100=9,26
Мо=2+5,5*(45-0) / (45-0)+(45-42)=7,16
Ме=7,5+5,5*(50-45)/42=8,15
R=35-2=33
l=(4,75-9,26)+(10,25-9,26)+(15,75-9,26)+(21,25-9,26)+(26,75-9,26)+(32,25-9,26)/100=0,55
Dх=(4,75-9,26)2*45+(10,25-9,26)2*42+(15,75-9,26)2*5+(21,25-9,26)2*4+(26,75-9,26)2*2+(32,25-9,26)2*2/100=34,11
δх=(34,11)1/2=5,8
V=5.8/9.26*100=62,63
1.5.2 Для дискретного ряда
Х=2*5+3*8+4*9+5*9+6*6+7*8+8*7+9*11+10*16+11*4+12*1+13*3+14*2+16*2+18*1+19*1+21*2+22*1+26*1+28*1+31*1+35*1/100=8,98
Мо=10
Ме=8
R=35-2=33
l=(2-8,98)+(3-8,98)+(4-8,98)+(5-8,98)+(6-8,98)+(7-8,98)+(8-8,98)+
(9-8,98)+(10-8,98)+(11-8,98)+(12-8,98)+(13-8,98)+(14-8,98)+(16-8,98)+
(18-8,98)+(19-8,98)+(21-8,98)+(22-8,98)+(26-8,98)+(28-8,98)+
(31-8,98)+(35-8,98)/100=1,22
Dx= (2-8,98)2+(3-8,98)2+(4-8,98)2+(5-8,98)2+(6-8,98)2+(7-8,98)2+(8-8,98)2+
(9-8,98)2+(10-8,98)2+(11-8,98)2+(12-8,98)2+(13-8,98)2+(14-8,98)2+
(16-8,98)2+(18-8,98)2+(19-8,98)2+(21-8,98)2+(22-8,98)2+(26-8,98)2+
(28-8,98)2+(31-8,98)2+(35-8,98)2/100=25,53
δх=(25,53)1/2=5,05
V=5,05/8,98*100=56,24