18В. Показательный (экспоненциальный) з.Р. Нсв

Непрерывная случайная величина имеет показательный закон распределения.

P(x)=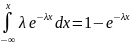

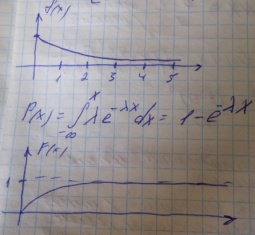
MX= ; DX=

Показательное распределение используется в приложениях теории вероятности, в теориях массового обслуживания, в теориях надежности.

19В.Нормальный закон распределения (Гаусса) нсв

Играет исключительную роль в Т вероятностей. Его главная особенность в том, что он является предельным законом к которому приближаются в определенных условиях другие законы распределения. Он наиболее часто встречается на практике.

Непрерывная СВ Х распределена по нормальному закону с параметрами а, , если ее плотность распределения имеет вид:

; ; DX= ; MX=a

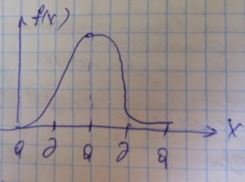
Нормальному закону подчиняется колебания курса акций, вес урожая, величины износа деталей.

20В.Двумерная св и функция ее распределения

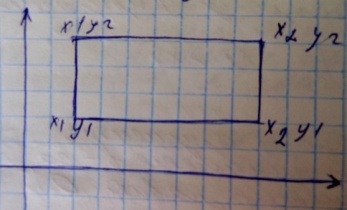
Рассмотрим испытание, результатом которого является появление двух чисел из некоторого конечного либо счетного множества пар чисел. Это испытание физически может быть одним испытанием (мгновенное измерение прибором величены тока и напряжения в сети), а также может быть композицией двух испытаний, каждое из которых порождает одномерную дискретную величину. Условно двумерная дискретная случайная величина обозначается как XY, либо любые две буквы латинского алфавита, либо для: X:{x₁, x₂, ...,x_s}, Y:{y₁, y₂, ...,y_n}, проводя испытание над двумерной случайной величиной находят одно из чисел из X либо из Y. А вероятностное пространство двумерной случайной величены формально строится так:

Двумерной случайной величиной называется система из двух одномерных случайных величин X, Y, где как X, так и Y являются дискретными случайными величинами. В пространстве элементарных событий дискретной случайной величены XY определим сложное событие A: В результате испытания над двумерной случайной величиной XY, случайная величина X приняла значение x_i, случайная величина Y - любое значение.

Зная закон распределения двумерной СВ можно найти закон распределения каждой из компонент.

Функцией распределения двумерной СВ называется функция F(x,y) которая для любых действительных чисел x,y равна вероятности совместного выполнения двух событий.

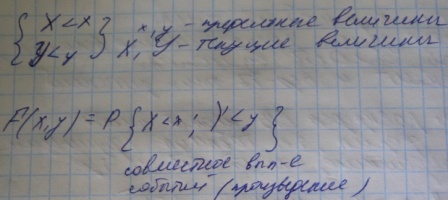
Геометрически эта функция интерпретируется как вероятность попадения случайной точки X и Y в бесконечный квадрат с вершиной в точке x,y.

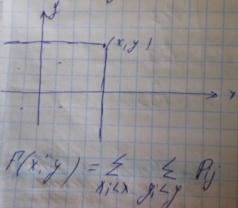
Свойства:

1) функция ограничена 0 F(x,y) 1

2) неубывающая по каждому из аргументов

3) если хотя бы один из аргументов функции обращается в бесконечность, то функция распределения равна 0

4) если оба аргумента обращаются в бесконечность, то функция распределения равна 1

5) если один из аргументов обращается в бесконечность, то функция становится функцией распределения соответствующей другому аргументу.

6) если функция непрерывна слева по каждому аргументу, то Х переходит в Х0.

С геометрической точки зрения это некоторая поверхность.