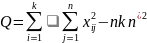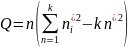38В.Критерий Пирсона

Разбив всю область СВ Х на n-интервалов 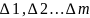, подсчитывают вероятности pi в каждом интервале по формуле:

Тогда теоретическое числовое значение СВ Х можно рассчитать по формуле: n∙pi

Таким образом, имеется эмпирический (статистический) ряд распределения СВ Х.

n1=np1	n2=np2	nm=npm

Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу Н0 следует отвергнуть, в противном случае принять.

Здесь необходим критерий, характеризующий степень расхождения между эмпирическими и теоретическими частотами. В качестве меры расхождения Пирсон предложил величину (критерий Пирсона).

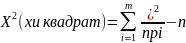
При n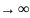 с k=m-r-1 степенью свободы, где m-число интервалов выборки, n-число параметров в предполагаемом распределении.

Правила применения критерия

1) вычисляем наибольшее

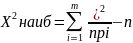
2) выбрав уровень значимости критерия по таблице находим критическую точку (квантель)

3) если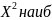 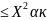, то гипотеза Н0 не противоречит опытным данным, в противном случае 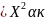, тогда гипотеза Н0 отвергается.

Необходимым условем пименения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений. Если в отдельных интервалах их оказывается меньше, то число интервалов нужно уменьшить путем их объединения.

39В.Дисперсионный однофакторный анализ

Например, требуется оценить влияние свойств сырья на показатели качества. В результате дисперсионного анализа может быть принято одно из двух решений (да∕нет).

Анализ можно проводить как по каждому фактору отдельно, так и по двум или нескольким одновременно.

В первом случае анализ называют однофакторным дисперсионным, во втором двухфакторным или многофакторным.

На каждом уровне сделаем n-измерение, получим совокупность измерений х_ij, где i=1,2…к; j=1,2… .

Обозначим через mi- мат.ожидание величины Х, при i-ом уровне фактора А.

Общее мат.ожидание – m, на основе экспериментальных данных требуется проверить гипотезу Н0 о равенстве всех мат.данных.

Н0: m1=m2=…=mk=m

Для проверки гипотезы вычисляется оценки мат.ожиданий на всех уровнях фактора и оценка общего мат.ожидания:

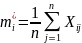
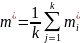
Идея дисперсионного анализа состоит в том, что сумма разбивается на 2 компоненты, одна из которых обуславливает влияние фактора А, другая-другие.

В результате получим:

Q=Q1+Q2

Q=

Q1=

Q2=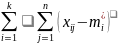

Компонента Q1 характеризует отклонение средних значений величины Х от общего среднего значения, т.е. характеризует влияние фактора.

Компонента Q2 указывает на рассеяние средней величины внутри уровня фактора. Величина Q2 называется остаточным рассеянием, а величина Q1 называется рассеянием по фактору.

Сравнивая эти 2 компоненты можно сделать вывод существенно ли влияние фактора А.

Величина Х по условию имеет нормальное распределение.

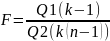
-если F F , то гипотеза принимается

-если F F , то гипотеза отвергается

При вычислении пользуемся формулами:

1)