36В. Доверительный интервал для мат ожидания при неизвестной дисперсии

Пусть случайная величина Х , где - неизвестна, -задана.

Вводим случайную величину:

S=

Теорема имеет распределение Стьюдента с n-1 степенью свободных.

Плотность этого распределения имеет вид:

Г(р)= – гамма функция

– четная функция.

Если перейти от к случайной величине Т, то:

- квантель уровня

По таблице квантелей распределения Стьюдента находятся значения в зависимости от числа степеней свободы n-1 и доверительной вероятности .

Зная , находим

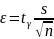
P

Следовательно, интервал показывает а= МХ с вероятностью , мы получим доверительный интервал для неизвестного математического ожидания случайной величины Х.

37В.Проверка стат. Гипотез о законе распределения

На практике часто встречаются задачи, связанные с принятием или отвержением некоторого предположения (гипотеза). Такие задачи требуют применения статистических методов. Процедура сопоставления предположения (гипотеза) с выборочными данными называется проверка гипотезы.

Эти задачи ставятся в следующем виде:

Относительно некоторой генеральной совокупности высказываются гипотезы Н0,Н1…Нn. Из генеральной совокупности извлекаются выборки, необходимо указать правило, при помощи которого по выборке решается вопрос об отклонении гипотезы Н или ее принятии. Статистическими методами гипотезу можно опровергать или подтверждать, но не доказывать.

После проверки делают вывод, что результат с гипотезой согласуется или не согласуется.

Гипотезы делятся на гипотезы о параметрах распределения известного вида (параметрические) и о виде неизвестного распределения (непараметрические).

Основной (нулевой) выделяют гипотезу Н0, конкурирующей (альтернативной) Н1, простой называют гипотезу содержащую только 1 предположение (МХ=а0), сложной – содержащую конечное или бесконечное число предположений (Н1: МХ ).

Имея 2 гипотезы Н0 и Н1 надо на основе выборки х1,х2…хn принять одну из них.

Статистическим критерием называют функцию выборки Tn=T(x1,x2…xn), множество Tn разбивается на 2 непересекающихся подмножества: критическую область S (область отклонения гипотезы Н0) и область (область принятия гипотезы Н0).

Если значения критерия попадают в критическую область S, то основная гипотеза Н0 отклоняется.

При проверке гипотез могут быть допущены ошибки двух видов:

1) отвергается правильная нулевая гипотеза Н0, ее вероятность .

2) отвергается правильная альтернативная гипотеза Н1, вероятность ее .

-уровень значимости критерия (0,05; 0,01; 0,005; 0,001).

Величина это вероятность недопущения ошибки второго рода (отвержение Н0 и принятие Н1 ). Это мощность критерия, чем она больше, тем вероятность ошибки второго рода меньше.

Одновременное уменьшение ошибок первого и второго рода возможно лишь при увеличении объема выборки.

Методика проверки гипотез

1) располагая выборкой формулируют нулевую Н0 и альтернативную гипотезу Н1.

2) В каждом конкретном случае подбирают статистику критерия, обычно из известных:

-распределение

U- нормальное распределение

t – распределение Стьюдента

F- распределение Фишера Снедока

Tn=T (х1,х2…хn)

3)По статистике критерия Tn и уровня значимости. Для каждого критерия имеются соответствующие таблицы.

4) Для получения выборки х=(х1,х2…хn) подсчитывают значения критерия

5) Если полученное значение принадлежит области , то нулевую гипотезу отвергают.