29. Оценка неизвестных параметров. Свойства статистических оценок.

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистическая оценка неизвестного параметра генеральной совокупности одним числом называется точечной. Рассмотрим следующие точечные оценки: смещенные и несмещенные, эффективные и состоятельные.

Для того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Укажем эти требования. Пусть 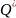есть статистическая оценка неизвестного параметра Q теоретического распределения. Допустим, что по выборке объема n найдена оценка 1. Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку 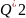и т. д. Получим числа 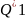, …которые будут различаться. Таким образом , оценку можно рассматривать как случайную величину, а числа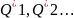 — как возможные ее значения.

Если оценка дает приближенное значение Q с избытком, то найденное по данным выборок число будет больше истинного значения Q . Следовательно, и математическое ожидание (среднее значение) случайной величины будет превышать Q , то есть . Если дает приближенное значение с недостатком, то .

Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки было равно оцениваемому параметру. Соблюдение требования устраняет систематические ошибки.

Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру Q, то есть .

Смещенной называют статистическую оценку , математическое ожидание которой не равно оцениваемому параметру.

Однако ошибочно считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия величины может быть значительной. В этом случае найденная по данным одной выборки оценка, например , может оказаться удаленной от своего среднего значения , а значит, и от самого оцениваемого параметра Q. Приняв в качестве приближенного значения Q , мы допустили бы ошибку. Если потребовать, чтобы дисперсия величины была малой, то возможность допустить ошибку будет исключена. Поэтому к статистической оценке предъявляются требования эффективности.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки ) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

30.Точечные оценки математического ожидания и дисперсии.

Задана случайная величина Х: х1, х2, …, хn, так как М(Х) не найти, то для математического ожидания случайной величины Х естественно предложить среднее арифметическое

1. По методу произведений

Это и означает, что оценка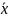 несмещенная.

2. Если исследуемая случайная величина Х имеет конечную дисперсию, то эта оценка будет состоятельной, так как

Точечная оценка для дисперсии

Так как дисперсия определяется через математическое ожидание, а для математического ожидания оценка уже выбрана, то для дисперсии естественно предложить оценку:

что соответствует записи дисперсии в виде

оценка дисперсии состоятельна и не является несмещенной.

Для получения несмещенной оценки введем поправку и полученную оценку обозначим через S2

Оценка S2 является состоятельной, так как сходится по вероятности к М(Х2), а – к М(Х).