28.Числовые характеристики статистического распределения.

Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной. Точечной оценкой генеральной средней является выборочное среднее .

Выборочным средним называется среднее арифметическое значение признака выборочной совокупности. Если все значения x1, x2,..., xn признака выборки различны (или если данные не сгруппированы), то:

Если же все значения признака x1, x2,..., xn имеют соответственно частоты n1, n2,..., nk, причем n1 + n2 +...+ nk = n (или если выборочное среднее вычисляется по вариационному ряду), то

В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего значениями вариант считают середины интервалов. Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0). Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения. Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году. Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Dв= -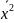

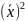
Несмещенная оценка дисперсии: 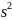= 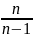*dв

Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.

Среднее квадратическое отклонение (стандартное отклонение), (от английского standard deviation) вычисляется как корень квадратный из дисперсии.

Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего. Непараметрическими характеристиками положения являются мода и медиана.

Модой Mo называется варианта, имеющая наибольшую частоту или относительную частоту.

Медианой Me называется варианта, которая делит вариационный ряд на две части, равные по числу вариант.

При нечетном числе вариант (n=2k+1)

Me = xk+1,

а при четном числе вариант (n=2k)

Me = (xk + xk+1)/2.