6. Відношення слідування і рівносильності між реченнями. Необхідні та достатні умови.

Якщо з твердження А випливає твердження В, то говорять, що В – необхідна умова для А, а А – достатня для В. іншими словами, вислів В називається необхідною умовою для А, якщо воно логічно випливає з А. вислів А називається достатньою умовою для В, якщо В з нього випливає. Якщо твердження А і В рівнозначні, то говорять, А – необхідна і достатня умова для В, і навпаки. Наприклад, в геометрії доведено, що з твердження «кути вертикальні» випливає твердження «кути рівні». тому згідно даному означенню можна сказати, що рівність кутів – необхідна умова для того, щоб кути були вертикальні, а вертикальність кутів є достатньою умовою для їх рівності. У зв‘язку з цим твердження «якщо кути вертикальні, то вони рівні» можна сформулювати інакше: для того, щоб кути були вертикальні, необхідно, щоб вони були рівні; для того, щоб кути були рівні, достатньо, щоб вони були вертикальні.

7.Структура та види теорем.

Раніше було відокремлено, що суттєві властивості об‘єкта утворюють зміст поняття про цей об‘єкт. Частина цих властивостей включається в означення поняття. Щоб мати більш повне уявлення про об‘єкт, вивчають і інші його властивості. Властивості основних (первісних) понять розкривається в аксіомах – твердженнях, які приймаються без доведення. Наприклад, властивості основних понять геометрії: точка, пряма, площини включені в аксіоми. Взагалі система аксіом будь-якої теорії, розкриваючи властивості основних понять, дає, по суті, їх означення, які називаються аксіоматичними. Властивості, які доводяться, найчастіше називають теоремами, іноді слідствами, признаками. В алгебрі – формулами, тотожностями, правилами. Тому, теорема – це висловлення про те, що з властивості А випливає властивість В. істинність цього вислову встановлюється шляхом доведення. В якому б виді не була сформульована теорема, в ній завжди виділяється умова А(що задано) і висновок В (що треба довести). Теореми і називаються оберненими одна до іншої, а теореми і називаються протилежними. Наприклад, для теореми «якщо кути вертикальні, то вони рівні» оберненою є «якщо кути рівні, то вони вертикальні», що являється хибність. Протилежною до заданої є «якщо кути не являються вертикальними, то вони не рівні» також є хибність. А ось обернена до протилежної «якщо кути не рівні, то вони не вертикальні» являється істиною. Встановлено, теореми і рівнозначні. Це називається законом контра позиції. Якщо задана теорема і і їй обернена являються вірними, то їх можна об‘єднати в одну за допомогою слів «тоді і тільки тоді» або «необхідно і достатньо».

8.Дедуктивні міркування. Найпростіші схеми дедуктивних міркувань.

• Дедуктивні міркування. Довести теорему - значить встановити логічним шляхом, що завжди, коли виконується властивість А, буде виконуватись і властивість В. доведення в математиці обладає рядом особливостей. Часто воно проводиться за правилами логіки без яких-то посилань на наглядність і дослід. В основі доведення лежить міркування – логічна операція, в результаті якої із одного чи декількох взаємозв‘язаних по змісту тверджень отримаємо твердження, яке містить нові (по відношенню до заданих) знання. В якості приклада розглянемо міркування першокласника, якому необхідно встановити відношення «менше» між числами 7 і 8. учень говорить: « , тому що 7 при рахунку називають раніше, ніж 8». На які ж факти він опирався, стверджуючи це. По-перше, якщо число а при рахунку називають раніше числа в, то 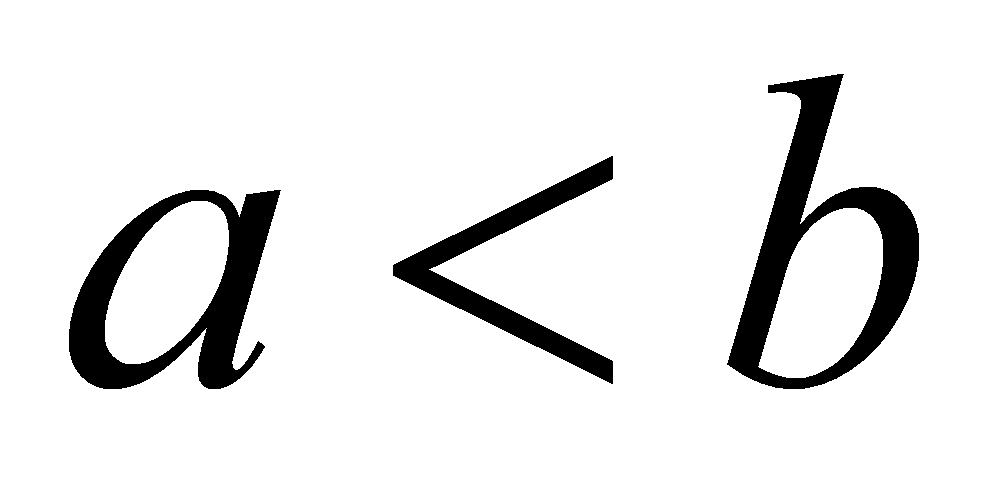для будь-яких натуральних чисел. І по-друге, 7 при рахунку називають раніше, ніж 8. перше твердження носить загальний характер, так як містить квантор спільності, його називають загальною посилкою. Друге твердження стосується конкретних чисел 7 і 8, відображає частинний випадок, його називають частковою посилкою. З двох посилок і випливає новий факт , його називають висновком. Міркування, між посилками і висновком якого має місце відношення слідування, називають дедуктивним. Іншими словами, міркування є дедуктивним, якщо за допомогою його з істинних посилок не можна отримати хибний висновок. Інакше міркування не являється дедуктивним.

Найпростіші схеми дедуктивних міркувань. Вважають, що в основі кожного дедуктивного міркування лежить певне правило висновку. 1) Правило висновку ( і , де - загальна посилка, - часткова посилка і - висновок. 2) Правило заперечення . 3) Правило силогізму . Застосування цих правил гарантує, що міркування буде дедуктивним, тобто дозволяє з істинних посилок виводити істинні висновки. Наприклад, 1) Всі числа, запис яких закінчується нулем, діляться на 5; число не ділиться на 5, значить, його запис не закінчується 0. 2) Якщо натуральне число кратне 8, то воно кратне 4; якщо натуральне число кратне 4, то воно кратне 2; значить, якщо число кратне 8, то воно кратне 2. 3) Якщо запис числа закінчується нулем, то воно ділиться на 5; число не закінчується нулем, значить, воно не ділиться на 5.