82.Функція.Поняття функції. Область визначення функції. Область означення функції.

Функція – це така відповідність між двома змінними, коли кожному значенню однієї змінної відповідає одне значення другої змінної.

Першу змінну називають незалежною, або аргументом функції, а другу – залежною- або функцією від першої змінної. Усі значення, які приймає незалежна змінна, утворюють область визначення функції.

Область визначення функції - це множина всіх значень змінної x, при яких функція має зміст.

З'ясуємо, як знайти область визначення деяких функцій, заданих формулою.

1. Якщо функція — многочлен, то вона існує при будь-яких значеннях аргумента, тобто її область визначення — всі дійсні числа.

2. Якщо функція задана формулою, яка містить аргумент у знаменнику дробу, то до області визначення функції входять всі дійсні числа, крім тих, які перетворюють знаменник в нуль.

3. Якщо функція задана формулою, яка містить арифметичний квадратний корінь, то до області її визначення входять всі дійсні числа, при яких підкореневий вираз набуває невід'ємних значень.

Область значень функції (множина значень) - усі значення, яких набуває функція.

Функція є парною - якщо для будь-якого х з області визначення функції виконується рівність f(x)=f(-x)

Функція є непарною - якщо для будь-якого х з області визначення функції виконується рівність f(-x)=-f(x)

83. Графік функції. Зростаюча, спадна функція, приклад.

Графіком функції y = f(x) називається множина всіх точок координатної площини (x, f(x)), у яких абсциси належать області визначення функції, а ординати дорівнюють відповідним значенням функції.  

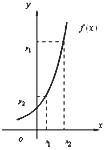
	Функцію y = f(x) називають зростаючою, якщо більшому значенню аргументу x відповідає більше значення функції y = f(x).
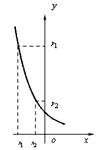
	Функцію y = f(x) називають спадною, якщо більшому значенню аргументу x відповідає менше значення функції y = f(x).

Якщо при деякому x функція y = f(x) набуває найбільшого значення, то цю точку називають точкою максимуму цієї функції і позначають x_max.

Якщо в точці x = x₀ функція y = f(x) набуває найменшого значення, то цю точку називають точкою мінімуму функції і позначають x_min. Точки максимуму і точки мінімуму називають точками екстремуму функції. Значення функції в цих точках позначають y_max і y_min.

84. Лінійна функція, її графік, її властивості.

Лінійною функцією називають функцію, що задається формулою y = bx + c, де x – аргумент; с, b - константи.

Якщо зокрема, k=0, то одержуємо сталу функцію y=b;

якщо b=0, то одержуємо пряму пропорційність y=kx.

Властивості функції y=kx+b

1.Область визначення - множина всіх дійсних чисел

2. Функція y=kx+b загального виду, тобто ні парна, ні непарна.

3. При k>0 функція зростає, а при k<0 спадає на всій числовій осі.

Графіком функції є пряма.

Наприклад, задано функцію y = 2x + 1.