43. Поняття текстової задачі. Способи розв’язування текстових задач.
У початковому навчанні математики значну роль відіграють текстові задачі.
Під математичною задачею розуміють будь-яку вимогу обчислити, побудувати, довести що-небудь, що стосується кількісних відношень і просторових форм, створених людським розумом на основі знань про навколишній світ.
Арифметичною задачею називають вимогу знайти числове значення деякої величини, якщо дано числове значення інших величин і існує залежність, яка пов’язує ці величини як між собою, так і з шуканою.
У системі навчання учнів початкових класів загальноосвітньої школи переважають арифметичні задачі. Задачі на побудову, найпростіші доведення, а також завдання логічного порядку займають порівняно незначне місце. Задачі з одного боку становлять специфічний розділ програми, матеріал якого учні мають засвоїти, а з другого – виступають як дидактичний засіб навчання, виховання і розвитку школярів. Отже, задачі мають такі функції, як:
пізнавальні, якими передбачається засвоєння елементів арифметичної теорії: зміст арифметичних дій, властивості арифметичних дій, взаємозв’язок між результатом і компонентами арифметичних дій, кількісні відношення між числами;
навчальні, які спрямовані на формування системи математичних ЗУН на різних етапах засвоєння;
виховні, що дають змогу пов’язати навчання з життям, ознайомити учнів з пізнавально важливими фактами, сприяють розвитку в учнів свідоме ставлення до навчання;
розвивальні, що спрямовані на формування в учнів науково – теоретичного (функціонального) стилю мислення, на оволодіння учнями прийомами розумової діяльності (аналізом, синтезом, конкретизацією, абстрагуванням, порівнянням, узагальненням), на висловлення власних суджень і міркувань.
У початкових класах, в основному, розглядають так звані сюжетні задачі, в яких описується кількісний бік якихось явищ, а знаходження невідомого зводиться до виконання певних арифметичних дій. В умові сюжетних задач подаються значення величин і деякі залежності (відношення) між цими значеннями, причому ці залежності мають певні числові характеристики.
Сюжетну задачу, для розв’язання якої треба виконати одну арифметичну дію, називають простою.
Сюжетну задачу називають складеною, якщо для її розв’язання виконують дві або більше арифметичних дій.
Структура текстової задачі:
умова (числові значення величин і описання залежності між ними);
питання (або вимога задачі – у наказовій формі формулювання);
розв’язання;
відповідь.
Вимоги до елементів задачі:
умова задачі повинна містити реальні поняття та їх числові характеристики;
умова задачі повинна бути логічно пов’язана із запитанням;
повинні існувати наявні відношення між даними в умові;
текст задачі лаконічний, правильно побудований з точки зору вимог мовлення.
Якщо завдання не відповідає якійсь з вимог до задач, його не вважають задачею. Наприклад:
1) Іван Царевич зірвав з першої яблуні 8 чарівних яблук, а з другої – 10. Скільки чарівних яблук зірвав Іван Царевич з третьої яблуні?
2) Мама купила 5 книжок. 2 книжки з’їли за обідом. Скільки книжок залишилося?
3) На дереві сиділо 8 риб, прилетіло ще 4. Скільки риб стало на дереві?
4) Скільки коштують 2 ляльки?
Етапи роботи над текстовою задачею:
1. Ознайомлення зі змістом задачі (читання вчителем, читання 1 учнем вголос, читання хором, самостійне читання учнями).
2. Бесіда за змістом задачі:
– Про що йдеться мова в задачі? (...)
– Що відомо? (...)
– Яке питання в задачі? (...)
3. Складання інтерпретації до задачі (порядкової, табличної, схематичної)
4. Повторення задачі вцілому.
5. Пошук розв’язання задачі.
6. Запис розв’язання і відповіді.
7. Творча робота над задачею.
Способи розв’язування текстових задач
Щоб розв’язати задачу, необхідно виконати вимогу задачі (дати відповідь на питання задачі) через логічно правильну послідовність дій та операцій над числами, величинами і залежностями, що задані в умові задачі
Способами розв’язування задач є:
арифметичний;
алгебраїчний;
графічний;
практичний.
При арифметичному способі відповідь на питання задачі знаходять в результаті виконання арифметичних дій над числами. Різні арифметичні способи розв’язання однієї і тієї ж задачі відрізняються відношеннями між відомими в задачі, відношеннями між відомими і шуканими величинами, послідовністю використання цих відношень при виборі виконання арифметичних дій.
Приклад. З одного куща смородини зібрали 18 кг ягід, а з другого – 12 кг. Усі ягоди розклали в ящики, по 6 кг у кожний. Скільки ящиків використали?
1 спосіб.
1) 18 + 12 = 30 (кг) – всього ягід;
2) 30 : 6 = 5 (ящ.)
2 спосіб.
1) 18 : 6 = 3 (ящ.) – для ягід з першого куща;
2) 12 : 6 = 2 (ящ.) – для ягід з другого куща;
3) 3 + 2 = 5 (ящ.)
При алгебраїчному способі відповідь на питання задачі знаходять в результаті складання та розв’язування рівняння.
Приклад. Катер пройшов відстань між пристанями за течією річки за 2 год, а назад – за 3 год. Знайдіть власну швидкість катера, якщо швидкість течії річки 2км / год.
Розв’язання. Нехай власна швидкість катера х км / год. Тоді
(х + 2) км / год – його швидкість за течією,
(х – 2) км / год – швидкість катера проти течії,
(х + 2) · 2 км – катер пройшов за течією,
(х – 2) · 3 км – катер пройшов проти течії.
Так як відстані (х – 2) · 3км та (х + 2) · 2км рівні, то маємо наступне рівняння: (х – 2) · 3 = (х + 2) · 2
3х – 6 = 2х + 4
х = 10
Отже, власна швидкість човна – 10км / год.
Для розв’язання наступної задачі розглянемо використання графічного і практичного способів.
Задача. У гаражі стояло 9 машин, із них 2 мікроавтобуси, 3 легкові, а решта – вантажні. Скільки вантажівок стояло у гаражі?
Графічний спосіб. Цей спосіб дає можливість відповісти на питання задачі, не виконуючи арифметичних дій. Для цього накреслимо відрізок довжиною 9 клітинок, так як загальна кількість машин – 9. Позначимо м – мікроавтобуси, л – легкові машини, в – вантажівки. Тоді
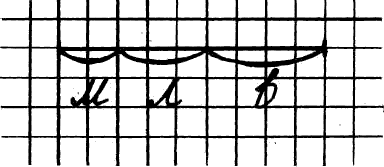
Отже, 4 вантажівки стояло у гаражі.
Практичний спосіб. Позначимо кожну машину квадратом. Тому намалюємо 9 квадратів, залишивши ті ж самі позначення: м, л та в.
Для відповіді на запитання також не треба виконувати арифметичні дій, бо кількість вантажівок можна одержати, порахувавши відповідні квадрати (їх 4).
45-46 Аналіз задачі і відшукання способів її розв'язування. Аналітичний пошук і синтетичний.Пошук способу розв'язування здебільшого проводять у процесі розбору задачі від числових даних до запитання (синтетичний спосіб) або від запитання до числових даних (аналітичний спосіб).
Суть відшукання способу розв'язування задачі від числових даних до запитання полягає в тому, що із сукупності числових даних складеної задачі вибираємо одну пару чисел і до неї ставимо відповідне запитання. Потім беремо другу пару чисел (одне з даних вже може бути результатом першої дії) і добираємо відповідне запитання. В такий спосіб утворюються прості задачі.
Особливість відшукання способу розв'язування задачі від запитання до числових даних полягає в тому, що спочатку визначають необхідні прості задачі (складають план розв'язування), а потім вже розв'язують задачу.
Спосіб розбору задачі від числових даних до запитання для дітей легший, але його застосування може давати зайві проби. Спосіб розбору задачі від запитання до числових даних більш цілеспрямований щодо складання плану розв'язування задачі, тут треба мати на увазі не одну яку-небудь дію, а хід міркування загалом. Однак для задач на три і більше дій він громіздкий.
Характеризуючи спосіб розбору задачі від запитання до числових даних, ми кожного разу для кожної простої задачі вказували обидві величини (відому і невідому). Такий розбір у літературі називають способом повного аналізу. Однак у практичній роботі під час розбору часто вказують лише невідому величину. Такий розбір називають просто аналізом (без терміна "повний").
Відшукання способу розв'язування задачі від запитання до числових даних.
Про що запитується в задачі? (Про кількість великих наметів). Чи можна про це дізнатися відразу? (Ні). Що треба знати, щоб дізнатися про кількість великих наметів? (Скільки всього ліжок було у великих наметах і скільки ліжок було у кожному великому наметі). Чи відомо, скільки ліжок було в кожному великому наметі? (Відомо). Чи відомо, скільки ліжок було у великих наметах? (Ні). Що треба знати, щоб дізнатися, скільки ліжок було у великих наметах? (Скільки всього ліжок було у таборі і скільки ліжок було в малих наметах). Чи відомо, скільки всього ліжок було у^таборі? (Відомо). Чи відомо, скільки ліжок було в малих наметах? (Ні). Чи можна230
Відшукання способу розв'язування задачі від числових даних до запитання задачі.
ТІ То відомо про малі намети? (У кожному малому наметі 4 ліжка, а всього таких наметів 12). Що можна знайти на підставі цих даних? (Кількість усіх ліжок у малих наметах). Якою дією? (Множення).
Якщо буде відомо, скільки було всього ліжок і скільки ліжок стояло в малих наметах, то про що тоді зможемо дізнатися? (Про кількість ліжок у великих наметах). Якою дією? (Віднімання).
Що тоді буде відомо про великі намети? (Кількість всіх ліжок у великих наметах і кількість ліжок в одному наметі). Про що зможемо дізнатися за цими даними? Якою дією? (Про кількість великих наметів у таборі. Для цього треба виконати дію ділення). В результаті цієї дії ми дізнаємося, скільки ^уло у таборі великих наметів.