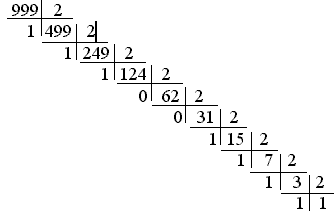38. Позиційна і непозиційна система числення. Запис чисел в десятковій системі числення. Запис чисел в різних позиційних системах числення, відмінних від десяткової.
Ідея нескінченності натурального ряду чисел освоювалось дуже повільно через відсутність протягом тривалого історичного періоду зручної системи числення. Перші системи числення були дуже недосконалими: для зображення кожного числа використовували окремий знак – ієрогліф. Пізніше ієрогліфи стали використовувати лише для позначення так званих вузлових чисел, решту чисел зображали за допомогою їх за принципом додавання або віднімання.
Зміст стародавньої єгипетської ієрогліфічної системи можна побачити у таблиці
I |
|
|
|
|
1 |
10 |
100 |
1000 |
10000 |
Стародавні єгиптяни лічили десятками. Але спеціальні знаки у них були лише для розрядів: одиниць, десятків, сотень і т. д. Числа від 1 до 10 записувались за допомогою паличок.
Наприклад, число 122 мало вид ς ∩∩I I .
У римський системі числення записували вузлові числа так: 1 - I, 5 – V, 10 – Х, 50 – L, 100 – C, 500 – D, 1000 – M. Решту чисел записували за принципом додавання або віднімання.
Наприклад, 256 – CCLVI, 399 – CCCXCIX.
Частково використовували і принцип множення: число 5 зображували символом руки, а 10 –як дві п’ятірки, тільки одна перевернута. Число 100 зображували буквою С, або (centum – сто), а 50 –L, як половину 100 (нижню половину).
Римською нумерацією користуємося і тепер. Ця система є непозиційною.
Непозиційними були також алфавітні системи: давньогрецька і старослов’янська. В цих системах перші 9 букв означали одиниці, наступні 9 – десятки, ще наступні – сотні.
У слов’янській нумерації було два способи лічби великих чисел: «мале словенське числення» і «велике словенське числення». У малому численні: 104 – тьма, 105 – легіон, 106 – леодр. У великому: тьма (@) – 106, легіон – 1012 – тьма тем, леодр – легіон легіонів – 1024, леодр леодрів – 1048 – ворон.
Перша позиційна система числення виникла понад 2000 років до н.е. в стародавньому Вавилоні. Це була шістдесяткова позиційна нумерація. Проте принцип позиційного значення цифр тут ще не використовувався скрізь. Для запису чисел використовували положення клину : ▼- 1 і 60, ◄ - 10. Інші числа зображувались за допомогою цих знаків і дій додавання.
Сучасна позиційна система числення була винайдена в Індії у V-VI ст. Через арабів вона поширилася в IX ст. в Середню Азію, а пізніше – і в Західну Європу. Великим досягненням індійської математики було введення нуля для позначення відсутності одиниць розряду в числі. Після цього десяткова система числення стала повністю оформленою. Запровадження десяткової системи числення на Русі було зупинено монгольським ігом. Тільки у XVIII ст. індійська система числення витіснила слов’янську нумерацію.
У сучасному житті використовують також інші системи числення. В астрономії з давніх-давен застосовується шістдесяткова система числення. Основою цієї системи є число 60. Так, 60сек = 1 мінута, або 60// = 1/, 60/ = 1° тощо.
Взагалі, основою числення може бути будь-яке натуральне число р ≥2. Для запису числа в такій системі числення використовується р символів: 0,1, ..., р-1.
Означення: Записом цілого невід’ємного числа х у р-й системі числення називається його подання у вигляді х = аnpn + … + a1p + a0, де an, …, a1, a0 набувають значення 0, 1, ..., р-1, аn ≠ 0 .
Числа 1, p, p2, … , pn називають розрядними одиницями 1-го, 2-го, ... , (n+1)-го розрядів.
Алгоритми переведення чисел з однієї позиційної системи числення в іншу
1. Для переведення чисел із системи числення з основою p в систему числення з основою q, використовуючи арифметику нової системи числення з основою q, потрібно записати коефіцієнти розкладу, основи степенів і показники степенів у системі з основою q і виконати всі дії в цій самій системі. Очевидно, що це правило зручне при переведенні до десяткової системи числення.
Наприклад:
з шістнадцяткової в десяткову:
92C816=9*10163+2*10162+C*10161+8*10160= 9*16103+2*16102+12*16101+8*16100=37576
з вісімкової в десяткову:
7358=7*1082+3*1081+5*1080= 7*8102+3*8101+5*8100=47710
з двійкової в десяткову:
1101001012=1*1028+1*1027+ 0*1026+1*1025+0*1024+0*1023+ 1*1022+0*1021+1*1020= 1*2108+1*2107+0*2106+1*2105+ 0*2104+0*2103+1*2102+0*2101+ 1*2100=42110
2. Для переведення чисел із системи числення з основою p в систему числення з основою q з використанням арифметики старої системи числення з основою p потрібно:
для переведення цілої частини:
послідовно число, записане в системі основою p ділити на основу нової системи числення, виділяючи остачі. Останні записані у зворотному порядку, будуть утворювати число в новій системі числення;
для переведення дробової частини:
послідовно дробову частину множити на основу нової системи числення, виділяючи цілі частини, які й будуть утворювати запис дробової частини числа в новій системі числення.
Цим самим правилом зручно користуватися в разі переведення з десяткової системи числення, тому що її арифметика для нас звичніша.
Приклади: 999,3510=1111100111,010112
для цілої частини:
