34. Теорема про існування частки та її єдність. Теорема про неможливість ділення на нуль.

3. Існування частки, її єдиність

Чи завжди існує частка натуральних чисел а і b? Відповідь на це запитання дає наступна теорема:

Теорема. Для того, щоб існувала частка двох натуральних чисел а і b, необхідно, щоб .

Доведення. Нехай частка натуральних чисел а і b існує, тобто існує таке натуральне число с, що . Для будь-якого натурального числа с правильне твердження . Помножимо обидві частини цієї нерівності на натуральне число b, отримаємо . Оскільки , то . Теорему доведено.

Чому дорівнює частка і натурального числа b? За означенням це таке число а, яке задовольняє умові . Так як , то рівність виконується, якщо . Отже, , якщо .

Теорема. Якщо частка натуральних чисел існує, то вона єдина.

Доведення (методом від супротивного). Припустимо, що існують дві частки і , тобто і . Нехай, наприклад, . Проте це суперечить властивості монотонності дії множення натуральних чисел. Отже, наше припущення, що існують два різних числа і , які є частками від ділення а на b, неправильне. Теорему доведено.

Із означення випливає, що:

а) частка від ділення натурального числа а на 1 дорівнює числу а, тобто ;

б) частка від ділення натурального числа а самого на себе дорівнює 1, тобто .

Розглянемо можливі два випадки.

1. Нехай .

Припустимо, що частка існує. За означенням частки через добуток , , тобто (за означенням добутку). Проте це суперечить умові про те, що . Отже, наше припущення, що частка існує, неправильне. Тому ділення на 0 в цьому випадку неможливе.

• Нехай .

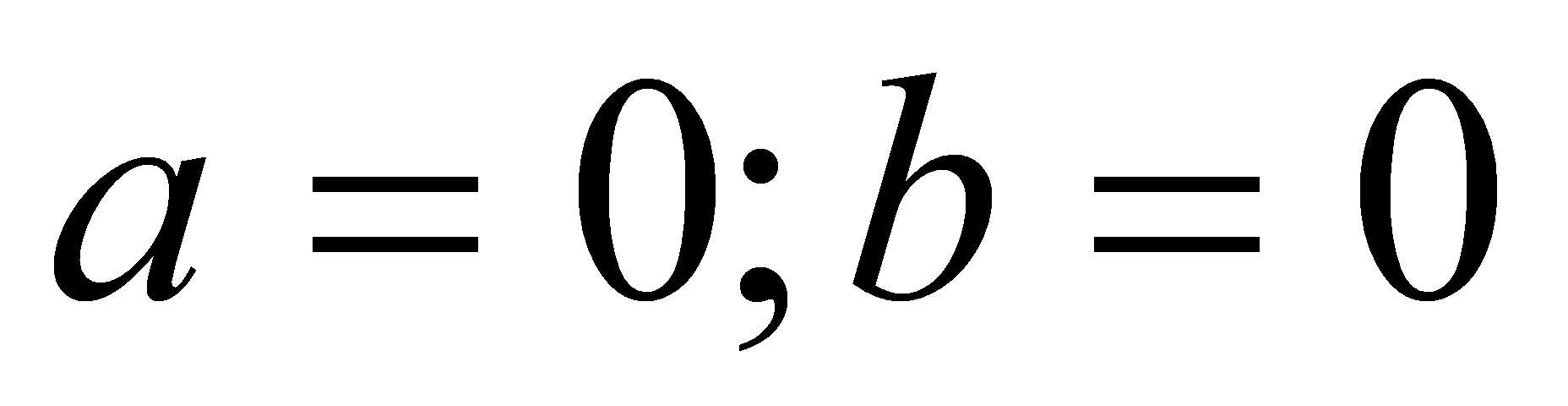Припустимо, що частка існує. За означенням частки через добуток , . З цього випливає, що будь-яке число с задовольняє умову , тобто частка визначена не однозначно. Це суперечить теоремі про єдиність частки. Отже, наше припущення, що частка існує, неправильне. Тому ділення на 0 і в цьому випадку неможливе.

Висновок: Ділення на нуль – неможливе.

35. Правила ділення суми та різниці на число.

1. Правило ділення суми на число.

Щоб поділити суму на число, досить поділити на це число кожний доданок і добуті результати додати: .

Доведення. Якщо рівність правильна, то за означенням дії ділення має бути:

(за розподільним законом множення);

(за властивістю ділення як дії, оберненої множенню).

Це правило можна поширити на будь-яке число доданків:

.

Правило ділення суми на число дуже важливе: воно є теоретичною основою алгоритму ділення багатоцифрових чисел.

У початкових класах його розкривають на конкретних задачах.

Задача. В одному сувої 12 м тканини, а в другому 15 м. з цієї тканини пошили плаття, витрачаючи на кожне по 3 м. Скільки платтів пошили?

Розв’язують задачу двома способами, дістаючи при цьому різні, але еквівалентні між собою числові формули розв’язку:

1-й спосіб 2-й спосіб

Висновок. .

2. Правило ділення різниці на число.

Щоб поділити різницю на число, досить поділити на це число зменшуване і від’ємник і від першого результату відняти другий: .

Пропонуємо довести це правило самостійно.

36. Правило ділення добутку на число. Правило ділення числа на добуток та множення числа на частку.

. Правило ділення добутку на число.

Щоб поділити добуток на число, досить поділити на це число один із множників і результат помножити на другий множник: .

Доведемо, наприклад, що . Якщо ця рівність правильна, то за означенням ділення .

4. Правило ділення числа на добуток.

Щоб поділити деяке число на добуток, досить поділити це число на один із множників і знайдену частку поділити на другий множник: .

На цьому правилі ґрунтується послідовне ділення при усних обчисленнях: .

37. ділення з остачею

Ділення одного натурального числа на інше ціле не завжди виконується. Тому розглядають більш загальну дію — ділення з остачею.

Поділити натуральне число на натуральне число з остачею — означає подати число у вигляді де і — невід’ємні цілі числа, причому Число при цьому називається неповною часткою, а число — остачею від ділення на Наприклад, при діленні числа 27 на 6 неповна частка дорівнює 4, а остача Щоб знайти ділене при діленні з остачею, потрібно неповну частку помножити на дільник і до здобутого добутку додати остачу. Очевидно, що тоді і тільки тоді, коли є дільником Ділення з остачею завжди виконується, про що свідчить наведена далі теорема (теорема про ділення з остачею).

Теорема. Для будь-яких натуральних чисел і існує єдина пара невід’ємних цілих чисел і , таких що

де